Development of a daily PM₁₀ and PM_2.5 prediction system using a deep long short-term memory neural network model

A deep recurrent neural network system based on a long short-term memory (LSTM) model was developed for daily PM₁₀ and PM_2.5 predictions in South Korea. The structural and learnable parameters of the newly developed system were optimized from iterative model training. Independent variables were obtained from ground-based observations over 2.3 years. The performance of the particulate matter (PM) prediction LSTM was then evaluated by comparisons with ground PM observations and with the PM concentrations predicted from two sets of 3-D chemistry-transport model (CTM) simulations (with and without data assimilation for initial conditions). The comparisons showed, in general, better performance with the LSTM than with the 3-D CTM simulations. For example, in terms of IOAs (index of agreements), the PM prediction IOAs were enhanced from 0.36–0.78 with the 3-D CTM simulations to 0.62–0.79 with the LSTM-based model. The deep LSTM-based PM prediction system developed at observation sites is expected to be further integrated with 3-D CTM-based prediction systems in the future. In addition to this, further possible applications of the deep LSTM-based system are discussed, together with some limitations of the current system.

1 Introduction

Over the past several decades, South Korea has made continuous economic growth; however, in accordance with this rapid economic development, emissions of air pollutants from various sources such as industrial, transportation, and power generation sectors have increased, and air quality has thus deteriorated (Wang et al., 2014). Among the atmospheric pollutants, particulate matter (PM) plays an important role in human health and climate change (Davidson et al., 2005; Forster et al., 2007). Several epidemiological studies have reported clear statistical relationships between aerosol concentrations and human mortality and morbidity (Dockery et al., 1992; Hope III and Dockery, 2006). To minimize the public damage caused by air pollution and to alert Korean citizens about high-PM events, the National Institute of Environmental Research (NIER) of South Korea has carried out daily air quality (or chemical weather) forecasting using multiple 3-D chemistry-transport models (CTMs) since 2014.

Figure 1 Schematic diagram of how the LSTM-based PM₁₀ and PM_2.5 prediction system was developed.

However, the accuracy of the 3-D CTM simulations has been reported to be low. Researchers believe that this low accuracy originates from uncertain sources of emission inventory, meteorological fields, initial and boundary conditions, and CTMs themselves (Seaman, 2000; Berge et al., 2001; Liu et al., 2001; Holloway et al., 2008; Tang et al., 2009; Han et al., 2011). Many efforts have been made to enhance the accuracy of the 3-D CTM-based forecasting system. As a part of the efforts, the Korean government decided to develop its own air quality forecasting system mainly based on a new CTM in 2017. This project entailed establishing better bottom-up and top-down emissions, developing improved meteorological fields over East Asia, developing a data assimilation system using satellite-retrieved and ground-based observations, and incorporating new atmospheric chemical and physical processes into the new Korean CTM. Despite all the ongoing efforts, the traditional chemical weather forecasts based on the CTM are still poor at conducting accurate air quality forecasts over South Korea.

Figure 2 Locations of NIER AIR KOREA and KMA AWS sites in South Korea.

In contrast, statistical models based on artificial neural networks (ANNs) have also been applied to air quality predictions. Because these approaches are based on a statistical method instead of sophisticated mathematical model-based computations (i.e., without considerations of advection and convection, photochemistry, or emissions), they are more cost-effective than 3-D CTM simulations. In previous studies, simple ANN models were applied to air quality predictions. The time-series concentrations of ambient pollutants have been predicted by, for example, supported vector machine (SVM) and radial basis function (RBF) neural network models (Lu and Wang, 2005). Furthermore, ambient levels of ozone were predicted by simple feed-forward neural network (FFNN) models (Yi and Rybutok, 1996; Abdul-Wahab and Al-Alawi, 2002). However, such simple models have the limitation of neglecting relationships among data at the different time steps. Recently, more complex ANN models have been developed with recurrent neural networks (RNNs). Although RNNs have typically been used for natural language recognition, they have the special advantage of remembering the experiences of past events because they maintain the activated vectors at each time step (Cho et al., 2014). Because of this advantage, RNNs also make accurate time-series predictions (Che et al., 2018). Several investigators used a shallow (single hidden layer) RNN model to predict the peak mixing ratios of ambient pollutants such as NO₂, SO₂, O₃, CO, and PM₁₀ (Brunelli et al., 2007), and others used a deep RNN model to predict ambient levels of PM_2.5 (Ong et al., 2016). However, RNN models have generally shown serious exploding and/or vanishing gradient problems (Bengio et al., 1994; Hochreiter, 1998). To resolve these problems, researchers developed the long short-term memory (LSTM) cell (Hochreiter and Schmidhuber, 1997). Unlike traditional RNNs, LSTM is known to be free from exploding or vanishing gradient problems, and it is better suited for long time-series predictions than are traditional RNNs. Recently, researchers used a deep LSTM neural network to conduct a number of air quality studies (Li et al., 2017; Freeman et al., 2018).

Although ANN-based predictions are not based on mathematics, deep learning has demonstrated a strong potential in the areas of weather and air quality forecasts; for example, the Weather Channel in the United States uses IBM Watson for its operational weather predictions (Mourdoukoutas, 2015). Another example is bias corrections based on several machine-learning techniques. Authors of one study reported that the biases (or errors) between the operational CTM-based air quality predictions and observations can be reduced by utilizing machine-learning algorithms (Reid et al., 2015). There must be many creative ways to improve the accuracy of air quality forecasts by combining 3-D CTM-based predictions with artificial intelligence (AI)-based techniques. These combined approaches have now begun, and this article intends to present one of these efforts in the area of air quality predictions.

For this study, we developed a deep LSTM model to more accurately predict ambient PM concentrations. We evaluated the model performance by comparing the CTM-predicted and observed PM₁₀ and PM_2.5 with the LSTM-predicted PM₁₀ and PM_2.5. The details of the system development and prediction procedures are presented in Sects. 2 and 3, and limitations of the model are discussed in Sect. 4.

2 Model development

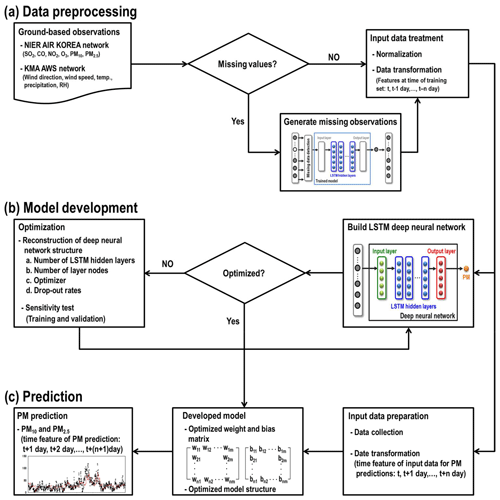
Figure 1 shows the schematic procedures for the deep LSTM-model-based PM predictions. There were two main processes in developing this prediction system: (i) data preprocessing and (ii) structure design and optimization of the deep neural network. It is essential to prepare time-series sequential data sets for both model training and predictions. In this study, we collected ambient pollutant concentrations and meteorological data from ground-based observations. To construct the system, we first screened several AI-based methods including LSTM, such as SVM, relevance vector machine (RVM), and a technique from convolutional neural network (CNN). Based on the results from the screening, we chose a multilayered deep LSTM neural network and conducted iterative model training to optimize the weights and biases of models at seven individual sites. We present the details on developing the system in the following sections.

2.1 Data preprocessing

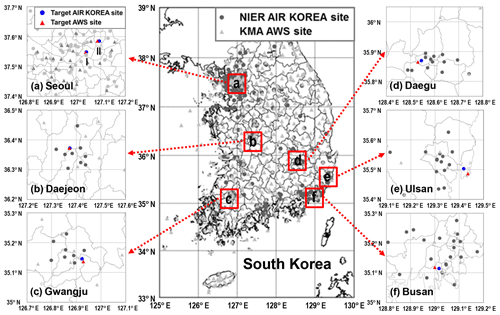
We collected the observation data from both the NIER AIR KOREA measurement network and the Korea Metrological Administration (KMA) automatic weather station (AWS) network to prepare the input variables. Figure 2 presents the locations of the AIR KOREA and KMA AWS observation sites throughout South Korea; the networks consist of 323 and 494 ground-based monitoring stations, respectively. They provide hourly mixing ratios of the ambient pollutants such as SO₂, CO, NO₂, O₃, PM₁₀, and PM_2.5 and the metrological parameters such as temperature, wind direction, wind speed, hourly precipitation, and relative humidity. PM₁₀ and PM_2.5 were measured by β-ray absorption and a gravimetric method, respectively (Shin et al., 2011). The ambient mixing ratios of SO₂, CO, NO₂, and O₃ were measured by pulse ultraviolet fluorescence, a nondispersive infrared sensor, chemiluminescence, and ultraviolet methods, respectively.

Among the observation sites, we chose seven monitoring sites located in the major cities in South Korea (Seoul (two sites), Daejeon, Gwangju, Daegu, Ulsan, and Busan) for PM₁₀ and PM_2.5 predictions (refer to Fig. 2a–f for the locations). There were two main criteria for selecting the seven sites: (i) the distances between air quality and meteorological monitoring stations should be the shortest (i.e., collocation) and (ii) the number of missing observation data should be minimal. Because there are sometimes too many missing values in the monitoring data prior to 2013, we used observations from January 2014 to April 2016 for training. After the model training, actual predictions of PM₁₀ and PM_2.5 were conducted for the period of the Korea-United States Air Quality (KORUS-AQ) campaign (from 1 May to 11 June 2016). The KORUS-AQ campaign period is now an official model testing window in South Korea.

The high quality of input data is critical for LSTM-based time-series predictions. In the current study, the missing values in ground-based air quality monitoring data were produced by using the pretrained deep LSTM model. The percentages of missing observations at the seven AIR KOREA sites are summarized in Table S1 in the Supplement. The percentage ranged between 0.7 % and 13.9 %. The schematic diagram of missing value generation is presented in Fig. S1 in the Supplement. As shown in Fig. S1, when the missing data were detected, the corresponding values were generated from a pretrained model. For example, the accuracy of the missing values generated for the Seoul-1 site is summarized in Fig. S2. It is shown from Fig. S2 that the pollutant concentrations generated by the pretrained model correlated well with the observed concentrations. The correlation coefficients for the model training and validation ranged from 0.60 to 0.91 and from 0.52 to 0.93, respectively. The accuracy of the generated missing values from the seven selected monitoring stations is summarized in Table S2. For the meteorological parameters, we determined the missing variables by interpolating the observed data; in the meteorological data, fewer than 0.01 % of values were missing.

In particular, information on various pollutants is important in the LSTM-based predictions of PM₁₀ and PM_2.5. Because H₂SO₄ and HNO₃ are main precursors of inorganic sulfate (${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$) and nitrate (${\mathrm{NO}}_{\mathrm{3}}^{-}$), respectively, correct information on the levels of their precursors (SO₂ and NO₂) is important. Although CO is not directly related to producing particulate matter, we included the mixing ratios in the input data because these are somehow related to the mixing ratios of ozone and hydroxyl radicals (OH).

Meteorological conditions also play an important role in particulate matter concentrations. Both wind direction and speed can represent the origin of air pollutants and intensity of atmospheric turbulence, and precipitation directly affects PM₁₀ and PM_2.5 by wet scavenging. In addition, there is a relationship between relative humidity and the levels of hydroxyl radicals because H₂O is a main precursor of OH. Water vapor can also influence the amounts of particulate water and nucleation rates in the atmosphere. Therefore, all meteorological parameters measured in the AWS monitoring data set can possibly affect PM concentrations, and thus we used them in the LSTM-based prediction system.

Table 1 Summary of model training and validation results.

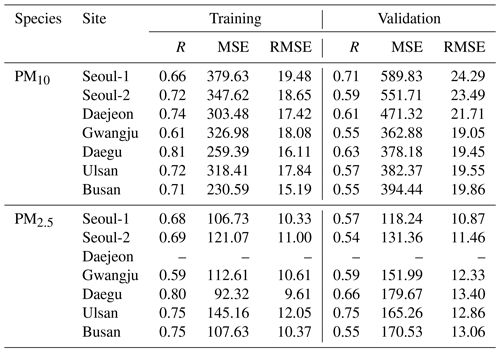
Note: the units for MSE and RMSE are in micrograms per cubic meter (µg m⁻³).

Before feeding the input variables into the LSTM system, one important step is data normalization. All the input parameters were rescaled between 0 and 1:

$$\begin{array}{}\text{(1)}& x_{\mathrm{normal},i}={\displaystyle \frac{x_i-x_{min,i}}{x_{max,i}-x_{min,i}}},\end{array}$$

where x_normal,i is the normalized values of species i; x_i is the observed value; and $x_{max,i}$ and $x_{min,i}$ are the maximum and minimum values of species i, respectively. Because the LSTM system was designed for daily prediction of PM₁₀ and PM_2.5, the normalized observations of the previous day were mapped with the PM concentrations of the next day (i.e., there is a 24 h time lag between independent and dependent variables). Thus, the shapes of one unit of training data are 24×11 and/or 24×12. This structured data set was then re-shaped as a three-dimensional vector matrix to feed them into the hidden LSTM layers. In addition, we excluded the observation data during the dust event periods in the model training; because these episodes are infrequent, including data on them could have interfered with establishing an accurate PM prediction system (i.e., they can be noisy signals).

Figure 3 Training and validating the daily PM₁₀ prediction model: (a) Seoul-1; (b) Seoul-2; (c) Daejeon; (d) Gwangju; (e) Daegu; (f) Ulsan; (g) Busan. Black and red dots represent the training and validation results, respectively.

2.2 System construction

As mentioned previously, the LSTM has the special advantage of remembering the past experiences. Because of this advantage, the LSTM has a strong capability for identifying highly complex relationship in the sequential data (i.e., the LSTM-based deep neural network has the strong potential in the time-series predictions). In general, the accuracy of the time-series prediction with the deep LSTM model is relatively higher than those with other deep neural networks (Ma et al., 2015; Amarasinghe et al., 2017). Several previous studies have proposed the use of the LSTM for more accurate time-series predictions (e.g., Connor et al., 1994; Saad et al., 1998). Based on this, in this study we used the LSTM cells in the construction of the deep hidden layers of daily PM₁₀ and PM_2.5 prediction model.

The developed system has two schemes: PM₁₀ prediction and PM_2.5 prediction; the prediction model is designed to have three to five hidden LSTM layers; one layer consists of 100 hidden nodes, and the layers capture sequential temporal information. The last LSTM hidden layer is connected to the output layer, which performs feature mapping between the output vectors from deep hidden layers and the actual PM₁₀ and/or PM_2.5.

In order to learn complicated and nonlinear mappings between the layers, activation functions are applied to get the output of a layer, which is then fed into the next layer as an input. There are several activation functions that can be used in neural networks; among them, a sigmoid function has been typically used because it has characteristics of being bounded and being differentiable; however, this function has a vanishing gradient problem due to continuous multiplication of gradients. In this study, therefore, we used the rectified linear unit (ReLU) to activate output layer (Nair and Hinton, 2010). The ReLU is expressed by

$$\begin{array}{}\text{(2)}& f\left(x\right)=\left\{\begin{array}{l}\mathrm{0}\mathrm{when}x<\mathrm{0}\\ x\mathrm{when}x\ge \mathrm{0}.\end{array}\right.\end{array}$$

As shown in Eq. (2), the ReLU ranges from 0 to ∞. Because the derivative of the ReLU is 0 or 1, the vanishing gradient does not occur during the back propagations. In the Supplement, we give a detailed description of the LSTM architecture used in this study.

In traditional statistics, the close relationship among the input variables (i.e., multicollinearity) can lead to instability of regression coefficients and can distort the effect of the regressive variables on dependent variables. For the deep learning, the multicollinearity requires a relatively long computation time because it is slow to converge. We evaluated the multicollinearity of the independent variables by estimating the Pearson correlation coefficient (R) between the observed atmospheric pollutants at the different time steps because the purpose of recurrent neural network is to identify the relationships in sequential data. The correlation coefficients are summarized in Table S3; as shown in Table S3, there are relatively low correlations among the concentrations of atmospheric pollutants. In addition, the LSTM-based deep neural network is effective for analyzing the relationships between highly correlated time-series sequential data (Fan et al., 2014). Furthermore, the problem of the multicollinearity can be resolved by adopting ReLU as an activation function (Ayinde et al., 2019).

Figure 4 Same as Fig. 3 but for PM_2.5.

2.3 Model training

The model training is a process for optimizing the structural and learnable parameters of the deep LSTM system; we determined the PM₁₀ and PM_2.5 prediction system's structure from the iterative training, and the structure was described in Sect. 2.2. In addition to the activation functions described in Sect. 2.2, there are two more main components in the deep neural network training: (i) cost function and (ii) optimization algorithm. The cost function usually measures how well the neural network works with respect to given training samples and corresponding predicted outputs. In other words, it is used for evaluating the accuracy of predicted values. When the prediction accuracy is poor, the cost is high, whereas as the model's predictions are more accurate, the cost decreases.

There are several cost functions commonly used in deep learning, and the cost function can be classified by its application purpose. In this study, the purpose of the cost function was to minimize the regression cost, and we thus used mean squared error (MSE) as a cost function, expressed as

$$\begin{array}{}\text{(3)}& J_{\mathrm{MSE}}\left(\mathit{\theta }\right)={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{\left(y_i-{\mathit{h}}_{\mathit{\theta }}\left({\mathit{x}}_i\right)\right)}^{\mathrm{2}},\end{array}$$

where x_i is the input vector for ith training; y_i is the target value (or true value) for the ith training; and h_θ(x_i) is the predicted vector corresponding to y_i for a given deep neural network model θ. It should be noted here that θ means the LSTM network with different parameters (see Eqs. S1–S6 in the Supplement). In Eq. (3), J_MSE(θ) represents the MSE between the target vector, y_i, and its predicted vector, h_θ(x_i), when the number of training vectors is N.

The role of an optimization algorithm is to find an efficient and stable pathway for minimizing the gradient descent of a cost function. In this study, we utilized adaptive moment estimation (ADAM) to train the neural networks (Kingma and Ba, 2015). The ADAM is one of the extended algorithms for stochastic gradient descent, and its detailed explanation is also given in the Supplement.

In order to train the LSTM system for the PM₁₀ and PM_2.5 predictions, the observations from January 2014 to April 2016 (2.3-year data) were used, as mentioned previously. Because Asian dust is regarded as containing noisy atmospheric signals, we removed the observations during dust events in the course of the model training. We divided the training data set into two groups with ratios of 0.85 to 0.15 for the model training and validation (Guyon, 1997).

First, we measured the variations in training and validation costs (i.e., the outcome of MSE cost) during the model training. In the early stages of the model training, updating the weights and biases decreases the training and validation costs. Because the training data set is only considered for updating weights and biases, the training cost is smaller than the validation cost. With the same reason, the training cost continues to decrease during the model training. In contrast, the validation cost decreases until a certain number of iterations, and then it starts to increase. Optimization of the deep neural network model is to update the weight and bias vectors until the validation cost reaches such an inflection point (Mahsereci et al., 2017). In addition, the model training can also be verified by comparing two statistical parameters, MSE and root mean squared error (RMSE); these values at the inflection point are summarized in Table 1. For properly trained models, the training cost should be slightly smaller than the validation cost. If the validation cost is much higher than training cost and the slope of validation cost is positive, it is called “over-fitting”, which means that both the weight and bias vectors of the model have been overturned. Based on the above two essential requirements of the model training, we concluded that our LSTM PM prediction model was well trained via general rules of the model training (refer to Table 1).

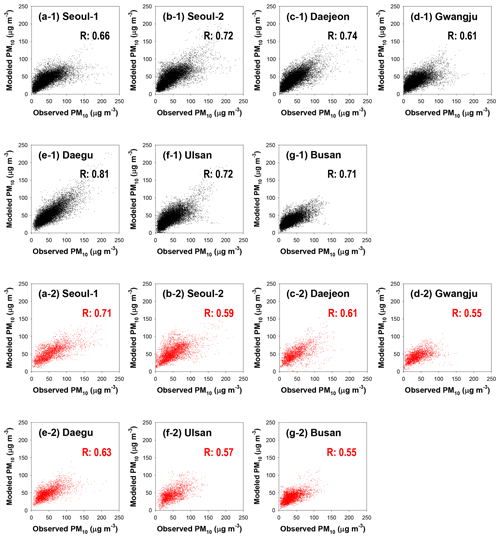
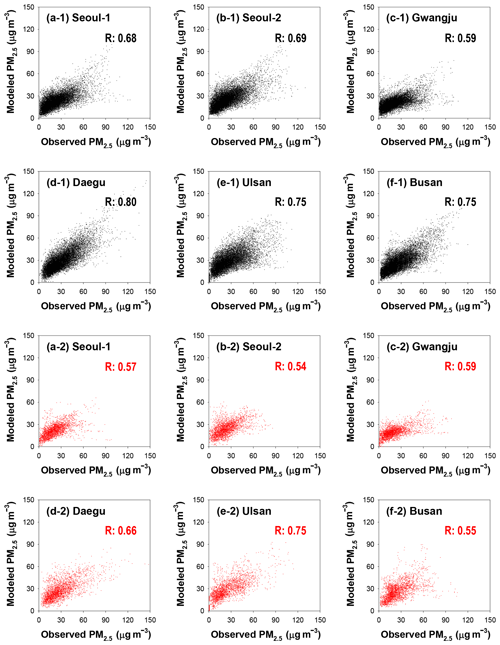
Second, the accuracy of the deep LSTM model training for PM₁₀ and PM_2.5 predictions is summarized in Figs. 3 and 4, respectively; in the figures, the black and red dots denote the comparison results between the predicted and observed PM concentrations in the model training and validation, respectively. As shown in Fig. 3, there was reasonable agreement in the PM₁₀ predictions. The R for PM₁₀ training and validation ranged from 0.61 to 0.81 and from 0.55 to 0.71, respectively. The training results for the PM_2.5 model also showed reasonable correlations (0.59≤R for training ≤0.80; 0.54≤R for validation ≤0.75).

2.4 3-D CTM simulations

In order to assess the accuracy of the LSTM-based predictions in this study, we compared them with 3-D CTM-based predictions with and without data assimilation (DA). We employed the Community Multiscale Air Quality (CMAQ) model v5.1 for the 3-D CTM simulations. We acquired the metrological fields from Weather Research and Forecasting v3.8.1 model simulations. The domain of the CMAQ model simulations is presented in Fig. 5; the model domain covers northeast Asia with a horizontal resolution of 15 km×15 km and with 27 sigma vertical levels. We used the KORUS v1.0 emission inventory for anthropogenic emissions; this inventory was made for the KORUS-AQ campaign based on three emission inventories: (i) CREATE (Comprehensive Regional Emission inventory for Atmospheric Transport Experiment); (ii) MICS-Asia (Model Inter-Comparison Study for Asia); and (iii) SEAC4RS (Studies of Emissions and Atmospheric Composition, Clouds, and Climate Coupling by Regional Surveys) (Woo et al., 2017). We estimated biogenic emissions from MEGAN v2.1 (Model of Emissions of Gases and Aerosols from Nature) simulations (Guenther et al., 2006). We obtained biomass burning emissions from FINN (Fire INventory from NCAR, http://bai.acom.ucar.edu/Data/fire/, last access: 13 October 2019) (Wiedinmyer et al., 2011). We obtained lateral boundary conditions from the MOZART-4 model simulations (https://www.acom.ucar.edu/wrf-chem/mozart.shtml, last access: 13 October 2019) (Emmons et al., 2010).

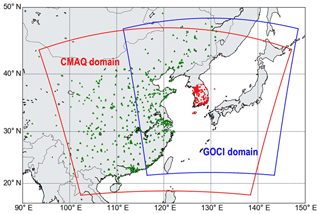
Figure 5 Domains of the CMAQ model simulations (red line) and Geostationary Ocean Color Imager (GOCI) sensor (blue line). Green triangles and red dots represent the locations of ground-based monitoring sites in China and South Korea, respectively.

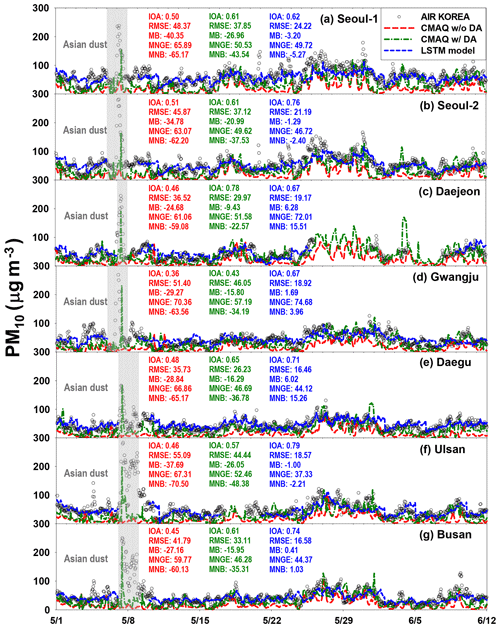
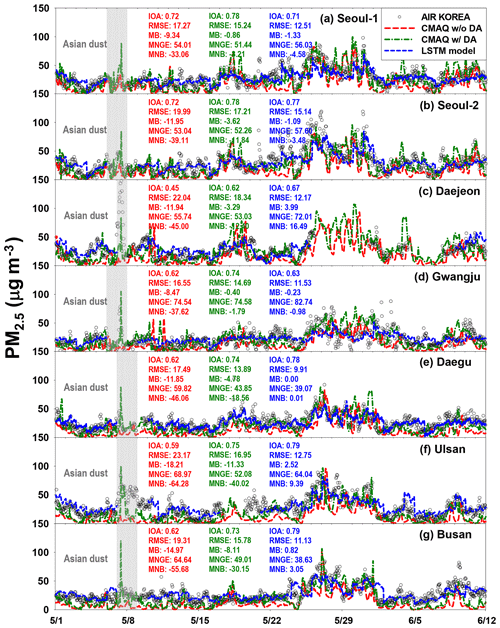
Figure 6 Comparisons between the CMAQ-calculated, LSTM-predicted, and the observed PM₁₀. Black open circles show observed PM₁₀ at seven sites. Dashed green and dashed red lines represent CMAQ-predicted PM₁₀ with and without data assimilation, respectively. Dashed blue lines represent LSTM-predicted PM₁₀. From 26 May to 7 June, the LSTM-based PM₁₀ predictions at the Daejeon site were not performed due to the continuous missing observations.

To prepare the initial conditions (ICs) for the CMAQ model simulations, we used the optimal interpolation with Kalman filter method (OI with Kalman). The DA with the OI technique has been used in several previous studies (Carmichael et al., 2009; Chung et al., 2010). The assimilation system is defined as follows:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{m}}{}^{\prime }={\mathit{\tau }}_{\mathrm{m}}+\mathbf{K}\left({\mathit{\tau }}_{\mathrm{o}}-\mathbf{H}{\mathit{\tau }}_{\mathrm{m}}\right),\text{(5)}& {\displaystyle }\mathbf{K}={\mathbf{BH}}^T{\left({\mathbf{HBH}}^T-\mathbf{O}\right)}^{-\mathrm{1}},\end{array}$$

where τ_m^′ represents the assimilated product; τ_o and τ_m denote the observed and modeled values, respectively; H represents the observation and/or forward operator; K represents the Kalman gain matrix; and B and O are the covariance of modeled and observed fields, respectively. B and O can be defined with several free parameters.

$$\begin{array}{}\text{(6)}& {\displaystyle }\begin{array}{rl}& \mathbf{B}\left(d_x,d_z\right)=\left[{\left(f_{\mathrm{m}}{\mathit{\tau }}_{\mathrm{m}}\right)}^{\mathrm{2}}+{\left({\mathit{\epsilon }}_{\mathrm{m}}\right)}^{\mathrm{2}}\right]\exp \left[-{\displaystyle \frac{d_x^{\mathrm{2}}}{\mathrm{2}{l}_{\mathrm{m}x}^{\mathrm{2}}}}\right]\\ & \exp \left[-{\displaystyle \frac{d_z^{\mathrm{2}}}{\mathrm{2}{l}_{\mathrm{m}z}^{\mathrm{2}}}}\right],\end{array}\text{(7)}& {\displaystyle }\mathbf{O}=\left[{\left(f_{\mathrm{o}}{\mathit{\tau }}_{\mathrm{o}}\right)}^{\mathrm{2}}+{\left({\mathit{\epsilon }}_{\mathrm{o}}\right)}^{\mathrm{2}}\right]\mathbf{I},\end{array}$$

where f_m, ε_m, d_x, d_z, l_mx, and l_mz represent the fractional error coefficient, minimum error coefficient, horizontal resolution, vertical resolution, horizontal correlation length for errors in modeled values, and vertical correlation length for errors in modeled values, respectively, and f_o, ε_o, and I denote the fractional error coefficient, minimum error coefficient in the observed values, and unit matrix, respectively. The six parameters in Eq. (6) are called the free parameters, which we used to calculate the observation and model error covariance matrix. In this study, we determined these parameters by finding the minimum of χ²:

$$\begin{array}{}\text{(8)}& {\mathit{\chi }}^{\mathrm{2}}=\sum {\displaystyle \frac{{\left(x_{\mathrm{obs}}-x_{\mathrm{assim}}\right)}^{\mathrm{2}}}{x_{\mathrm{assim}}}}.\end{array}$$

Here x_obs and x_assim represent the observed and data-assimilated values, respectively. More detailed explanations regarding the data assimilation can be found elsewhere (Collins et al., 2001; Yu et al., 2003; Park et al., 2011).

Figure 7 Same as Fig. 6 but for PM_2.5.

For the DA runs, we integrated the CMAQ model simulations with three observation data sets: (i) the Communication, Ocean and Meteorological Satellite (COMS) Geostationary Ocean Color Imager (GOCI) aerosol optical depth (AOD); (ii) ground-based observations in China; and (iii) AIR KOREA observations in South Korea. The locations of the observation stations are presented in Fig. 5. Because the GOCI sensor is geostationary, it can provide hourly spectral images with spatial resolution of 500 m×500 m from 00:00 to 07:00 UTC. Detailed procedures can also be found in previous publications (Park et al., 2014a, b).

3 Results and discussion

PM₁₀ and PM_2.5 were predicted for the period of the KORUS-AQ campaign. To evaluate the performance of the LSTM system, we compared the LSTM-based predictions with the observations and two CMAQ-based predictions.

3.1 System evaluation

We evaluated the accuracy of the LSTM-based PM predictions by comparing them with the observed PM₁₀ and PM_2.5. We also compared PM₁₀ and PM_2.5 predicted from two sets of CMAQ model simulations with the PM₁₀ and PM_2.5 predicted from the deep LSTM; these results are presented in Figs. 6 and 7. In Figs. 6 and 7, the black circles and dashed blue lines represent the observed and LSTM-predicted PM₁₀ and PM_2.5, respectively. The dashed green and dashed red lines denote CMAQ-predicted PM₁₀ and PM_2.5 with and without DA, respectively. The CMAQ model simulations with DA showed better agreement with the observations than did those without DA (see Figs. 6 and 7). The LSTM-predicted PM₁₀ also showed good agreement with the observed PM₁₀.

Table 2 Statistical analysis with modeled and observed PM₁₀ and PM_2.5.

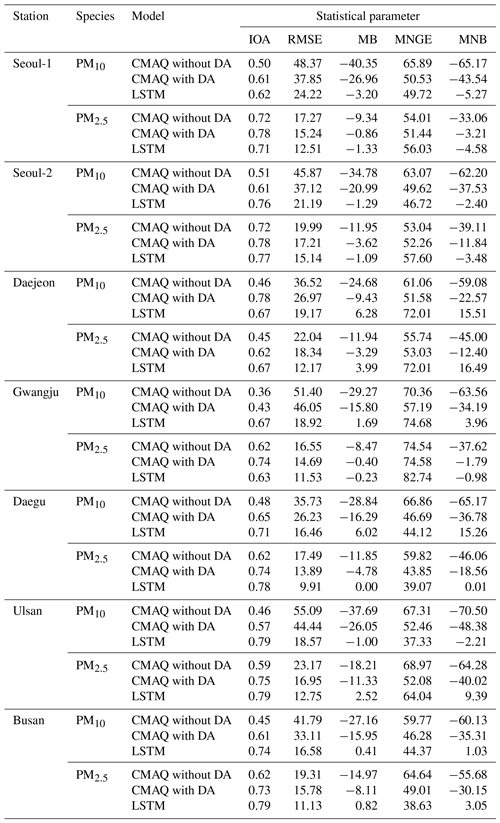
Note: the units for RMSE and MB are micrograms per cubic meter (µg m⁻³) and those for MNGE and MNB are in percent (%).

However, the results from the CMAQ model simulations were not intended to be directly compared with those from the LSTM predictions. In general, Eulerian CTMs calculate average concentrations of air pollutants in a grid box, but in the real world the concentrations of air pollutants inside a gird box can be (highly) variable with proximity to the local sources (in other words, the air pollutant concentrations in a gird box cannot be uniform). This is well-known problem called “sub-grid variability”. In this sense, both the CMAQ-model results and LSTM predictions were not directly compared. Instead, in this comparison the CMAQ model simulations provide reference values to give a sense of the accuracy of LSTM predictions. One intension to develop the LSTM prediction system is to establish a prediction system at the observation sites (i.e., point site), and we eventually plan to integrate the CTM-LSTM prediction (gird-based prediction and point-based prediction) system for more comprehensive PM forecasting in South Korea. This will be discussed further in Sect. 4.

Figure 8 Percentage (%) of high-particulate-matter episodes in the training data set.

For further statistical evaluations, we introduced the following five statistical parameters: (i) IOA (index of agreement); (ii) RMSE; (iii) MB (mean bias); (iv) MNGE (mean normalized gross error); and (v) MNB (mean normalized bias).

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathrm{IOA}=\mathrm{1}-{\displaystyle \frac{\sum _{\mathrm{1}}^N{\left(C_{i,\mathrm{Model}}-C_{i,\mathrm{Obs}}\right)}^{\mathrm{2}}}{\sum _{\mathrm{1}}^N{\left(\left|C_{i,\mathrm{Model}}-\stackrel{\mathrm{‾}}{C_{i,\mathrm{Obs}}}\right|+\left|C_{i,\mathrm{Obs}}-\stackrel{\mathrm{‾}}{C_{i,\mathrm{Obs}}}\right|\right)}^{\mathrm{2}}}},\text{(10)}& {\displaystyle }\mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\sum _{\mathrm{1}}^N{\left(C_{i,\mathrm{Model}}-C_{i,\mathrm{Obs}}\right)}^{\mathrm{2}}},\text{(11)}& {\displaystyle }\mathrm{MB}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{\mathrm{1}}^N\left(C_{i,\mathrm{Model}}-C_{i,\mathrm{Obs}}\right),\text{(12)}& {\displaystyle }\mathrm{MNGE}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{\mathrm{1}}^N\left({\displaystyle \frac{\left|C_{i,\mathrm{Model}}-C_{i,\mathrm{Obs}}\right|}{C_{i,\mathrm{Obs}}}}\right)\times \mathrm{100},\text{(13)}& {\displaystyle }\mathrm{MNB}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{\mathrm{1}}^N\left({\displaystyle \frac{C_{i,\mathrm{Model}}-C_{i,\mathrm{Obs}}}{C_{i,\mathrm{Obs}}}}\right)\times \mathrm{100}.\end{array}$$

Here, C_i,Model and C_i,Obs represent the modeled and observed concentrations of species i; $\stackrel{\mathrm{‾}}{C_{i,\mathrm{Obs}}}$ is the averaged C_i,Obs. The results from the statistical analysis are summarized in Table 2 and are also shown in Figs. 6 and 7.

For the daily PM₁₀ predictions, the LSTM-based predictions (0.62≤ IOA ≤0.79) were always more accurate than two CMAQ-based PM₁₀ predictions (0.36≤ IOA ≤0.78). RMSE and MB between the CMAQ-based and observed PM₁₀ ranged between 33.11 and 51.40 µg m⁻³ and between −40.35 and −15.95 µg m⁻³, respectively. These negative MBs indicate that the CMAQ model simulations underestimated PM₁₀. RMSE and MB between the LSTM-based predictions and observations ranged from 18.57 to 24.23 µg m⁻³ and from −3.20 to 6.28 µg m⁻³, respectively. The RMSEs for the LSTM-based predictions are 1.90 times smaller than those for the CMAQ-based predictions. Among the seven sites chosen, the PM₁₀ predictions at the Daegu, Ulsan, and Busan sites showed the best agreement (0.71≤ IOA ≤0.79) and the lowest errors and biases (16.46≤ RMSE ≤18.57; $-\mathrm{1.00}\le$ MB ≤6.02) compared with the two CMAQ-based PM₁₀ predictions (0.45≤ IOA ≤0.65; 26.23≤ RMSE ≤55.09; $-\mathrm{37.69}\le$ MB $\le -\mathrm{15.92}$).

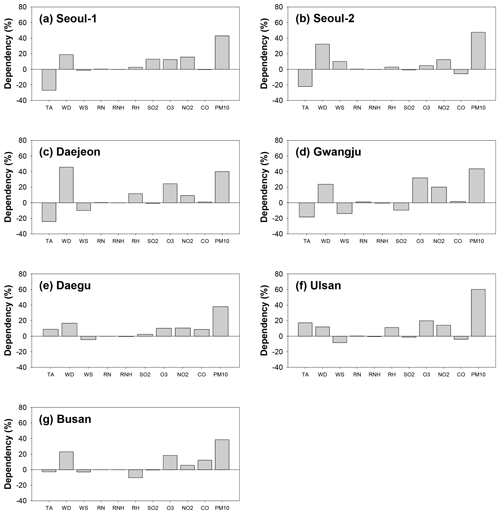
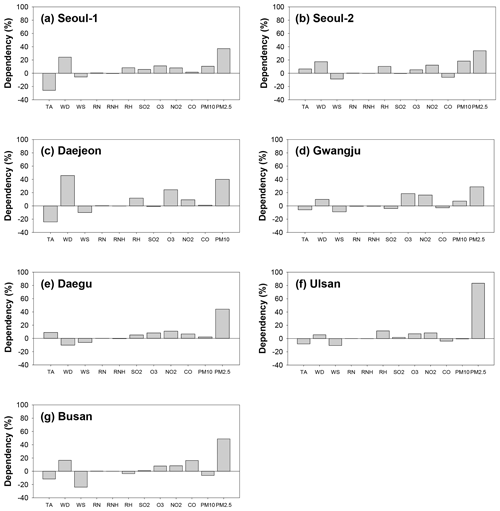
Figure 9 Dependencies of input variables on the daily PM₁₀ predictions. TA, WD, WS, RN, RNH, and RH represent temperature, wind direction, wind speed, daily cumulative precipitation, hourly precipitation, and relative humidity, respectively. SO₂, O₃, NO₂, CO, and PM₁₀ refer to the levels of the previous day for these atmospheric pollutants.

Figure 7 presents the comparisons for PM_2.5. During the KORUS-AQ campaign, there were no ground PM_2.5 observations at the Daejeon site between 1 May and 11 June because of instrument malfunction. The LSTM-predicted PM_2.5 again showed good agreement with the observations (0.63≤ IOA ≤0.79); however, the deep LSTM system was not always able to more accurately predict PM_2.5. As with PM₁₀, the LSTM PM_2.5 predictions at the Daegu, Ulsan, and Busan sites showed better performance (0.78≤ IOA ≤0.79) than the CMAQ-based predictions (0.59≤ IOA ≤0.75), but at the two Seoul sites (Seoul-1 and Seoul-2) the LSTM PM_2.5 predictions were inferior to those from the CMAQ model simulations with DA (dashed green lines in Fig. 7). This could have been because the AIR KOREA observation sites are densely located in and around Seoul Metropolitan Area (refer to Fig. 2). Therefore, data assimilation appears to more strongly influence the accuracy of the CMAQ predictions.

Figure 10 Same as Fig. 9 but for PM_2.5.

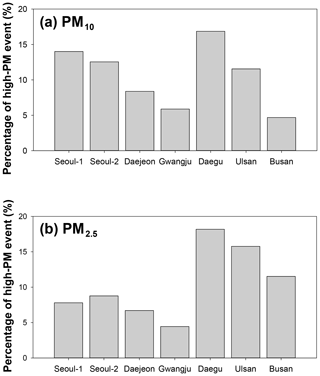
As shown in Figs. 6 and 7, there were nationwide high-PM episodes from 25 to 28 May 2016; these high-PM events were caused by the long-distance transport of atmospheric pollutants from China due to westerlies, and the relatively high errors and biases in the LSTM-based predictions occurred during these high-PM events. Because the model's weights and biases were optimized based on previous memories, frequent high-PM episodes can affect the accuracy of the predictions. The frequencies of the high-PM₁₀ (daily average of PM₁₀ ≥70 µg m⁻³) and high-PM_2.5 (daily average of PM_2.5 ≥40 µg m⁻³) episodes in the training data set are summarized in Fig. 8. The fractions of the high-PM_2.5 episodes at the Seoul and Gwangju sites were between 0.04 and 0.09, clearly smaller than those at Daegu, Ulsan, and Busan (0.12≤ high-PM_2.5 episode ≤0.18). At Gwangju, the effectiveness of DA and frequency of high-PM episodes were the lowest. As mentioned previously, the LSTM-based PM₁₀ and PM_2.5 prediction system was trained using the observation data for only 2.3 years because these were the only available data. The optimized weights and biases are governed by the variety of input features in the training. If more PM_2.5 data are available in the future, the prediction accuracy of deep LSTM systems will improve; and in fact, continuous data accumulation with more recent PM data is now underway.

Imbalance of the training data set has deteriorated the performances of the deep neural network model. As shown in Fig. 8, the frequency of high-PM₁₀ and high-PM_2.5 events is very low. There are a number of ways to balance the data, such as minority oversampling and majority subsampling. The prerequisite for the data balancing is that the amounts of available data should be very large. As mentioned previously, the AIR KOREA network has monitored ground PM_2.5 only since 2015. Therefore, the amount of available data is relatively small, and compulsory data balancing is highly likely to hinder the generalization of the PM prediction model. Therefore, we did not perform the data balancing in this study.

To test the effectiveness of the data balancing, we did balance the data for the observations of the Seoul-1 site; at this site, the CMAQ-based PM_2.5 predictions were better than the LSTM-based PM_2.5 predictions. Because of the data availability, it was impossible to balance the training data set with the subsampling method, and thus we oversampled atmospheric conditions during the high-PM_2.5 events. To balance the numbers of high-PM and non-high-PM events, we replicated the ground observations during the high PM_2.5 events; then we generated ±5 % Gaussian random noise on these oversampled data to reflect the observational errors. The PM_2.5 predictions with and without the data balancing are represented in Fig. S4. As shown in Fig. S4, the data balancing did not improve the prediction performances of the LSTM model. This is because we could not sample the various types of high-PM_2.5 events, and similar patterns of atmospheric conditions were consistently considered in the model training. Therefore, to improve the performances of the LSTM-based PM prediction model, it is necessary to collect various atmospheric conditions through continuous ground-based observations.

3.2 Dependence on input parameters

In deep learning, the relationships between input variables and predictions cannot be identified directly because of the high nonlinearity in the hidden layers. In the present study, we indirectly investigated the influences of the input parameters on the PM₁₀ and PM_2.5 predictions with and without considering each variable in the model operations. The influences on the input parameters are summarized in Figs. 9 and 10; in the figures, TA, WD, WS, RN, RNH, and RH represent temperature, wind direction, wind speed, daily cumulative precipitation, hourly precipitation, and relative humidity on the previous day, respectively. SO₂, O₃, NO₂, CO, PM₁₀, and PM_2.5 are the concentrations of the respective air pollutants on the previous day. The positive and negative values in each figure represent the directionality of the influences on the PM₁₀ and PM_2.5 predictions; that is, for instance, the variables with positive dependence indicate increasing influence on the predicted PM₁₀ and PM_2.5. The figures show that among the meteorological variables, temperature and wind direction generally had great influence on the PM₁₀ and PM_2.5 predictions; among the pollutant variables, previous day PM₁₀ and PM_2.5 mainly affected the predictions for the next day. In particular, the dependencies of PM₁₀ and PM_2.5 ranged from 38.48 % to 60.12 % and from 28.80 % to 83.38 %, respectively. In most cases, the influence of the pollutant variables (PM₁₀ and PM_2.5) was greater than that of the meteorological parameters. However, at Daejeon, the most influential parameter on the PM₁₀ predictions was wind direction (45.67 %), while the contributions of other parameters were relatively small. The difference in the contributions is mainly due to the persistence of each variable. In other words, the variables with low dependence on the PM₁₀ and PM_2.5 predictions were those that change rapidly in the atmosphere, and thus their effects are scarcely incorporated into the trained model.

4 Outlook and future works

In this study, we established a deep RNN system for daily PM₁₀ and PM_2.5 predictions and evaluated the newly developed system's performance by comparing its PM₁₀ and PM_2.5 predictions with the observed and CMAQ-predicted levels. In the comparisons, the LSTM-based PM predictions were, in general, superior to the CMAQ-based PM predictions. In terms of IOA, the accuracies of the LSTM predictions were 1.01–1.72 times higher than those for the CMAQ-based predictions. Based on this, we concluded that the LSTM-based system could be applied to daily “operational” PM₁₀ and PM_2.5 forecasts. The LSTM-based predictions at the observation sites can provide useful and complementary information for air quality forecasters, synthesizing all the information available such as CTM air quality predictions, AI predictions, weather predictions, and satellite-derived information.

In the future, Korea's air quality forecasting system will be improved by continuous development of the CTM-based prediction system including the use of more advanced DA techniques, together with continuous sophistication of the AI-based prediction system. If the AI-based predictions at the observation sites are consistently better than the CTM-based predictions, the two elements will be more systematically combined within a prognostic mode, which will be our final research goal. In addition, a similar LSTM-based prediction system can also be applied to the daily forecasts of gas-phase air pollutants such as NO₂, SO₂, CO, and O₃. These works are also now in progress.

Although the current LSTM-based system can accurately predict PM₁₀ and PM_2.5, it also has some limitations. For better prediction accuracy, we need more air quality data for model optimization. Because PM_2.5 has only been monitored in South Korea since 2015, there are too few observations to optimize the PM_2.5 predictions, which require continuous accumulation of PM_2.5 observations. In addition, the limited number of input variables is another obstacle to optimal model performance. The current LSTM-based PM₁₀ and PM_2.5 prediction system contains 10–12 input parameters. If more useful parameters such as mixing layer height (MLH) and barometric distribution are available, its performance would improve further (Hooyberghs et al., 2005; Liu et al., 2007). Therefore, future efforts should be made with more PM_2.5 data and more input variables such as mixing layer heights entered into our system.