the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Comparison of equatorial wave activity in the tropical tropopause layer and stratosphere represented in reanalyses
George N. Kiladis
John R. Albers
Juliana Dias
Masatomo Fujiwara
James A. Anstey
In-Sun Song
Corwin J. Wright
Yoshio Kawatani
François Lott
Changhyun Yoo
Equatorial Kelvin and mixed Rossby–gravity (MRG) waves in the tropical tropopause layer and stratosphere represented in recent reanalyses for the period of 1981–2010 are compared in terms of spectral characteristics, spatial structures, long-term variations, and their forcing of the quasi-biennial oscillation (QBO). For both wave types, the spectral distributions are broadly similar among most of the reanalyses, while the peak amplitudes exhibit considerable spread. The longitudinal distributions and spatial patterns of wave perturbations show reasonable agreement between the reanalyses. A few exceptions to the similarity of the spectral shapes and spatial structures among them are also noted. While the interannual variations of wave activity appear to be coherent for both the Kelvin and MRG waves, there is substantial variability in long-term trends among the reanalyses. Most of the reanalyses which assimilate satellite data exhibit large increasing trends in wave variance (∼15 %–50 % increase in 30 years at 100–10 hPa), whereas one reanalysis (Japanese 55-year Reanalysis assimilating conventional observations only; JRA-55C) produced without satellite data does not. Several discontinuities are found around 1998 in the time series of the Kelvin and MRG wave variances, which manifest in different ways depending on the reanalysis, and are indicative of impacts of the transition of satellite measurements during that year. The equatorial wave forcing of the QBO, estimated by the Eliassen–Palm (EP) flux divergence, occurs in similar phase-speed ranges in the lower stratosphere among the reanalyses. However, the EP flux and its divergence are found to be dependent on the zonal-mean winds represented in reanalyses, exhibiting different magnitudes, altitudes, and phase-speed ranges of the Kelvin wave forcing between the reanalyses, especially at 20–10 hPa. In addition, at around 20 hPa, a wave signal which appears only in easterly mean winds with westward phase speeds is found and discussed.
- Article
(17001 KB) - Full-text XML
-
Supplement
(1197 KB) - BibTeX
- EndNote
Stratospheric equatorial waves are known to be generated in response to the heat sources associated with tropical convection and to play an important role in the tropics (Salby and Garcia, 1987; Garcia and Salby, 1987). On subseasonal timescales, Kelvin waves lead to large variations in tropopause temperature and height (e.g., Tsuda et al., 1994; Kim and Son, 2012; Kim and Alexander, 2015) and modulate the formation of cirrus clouds (Boehm and Verlinde, 2000; Immler et al., 2008). Kelvin waves in the tropical tropopause layer (TTL) are also important in stratosphere–troposphere exchange, as they modulate the amount of water vapor entering the stratosphere via dehydration of air and transport and mixing of chemical species such as ozone via wave breaking (Fujiwara et al., 1998, 2001; Plumb, 2002; Fueglistaler et al., 2009). It has been observed that mixed Rossby–gravity (MRG) wave circulations in the lower troposphere are related to tropical cyclogenesis (Dickinson and Molinari, 2002; Zhou and Wang, 2007). In the stratosphere, the Kelvin and MRG waves, along with smaller-scale waves, are known as sources of momentum needed to drive the easterly-to-westerly and westerly-to-easterly phase transitions of the quasi-biennial oscillation (QBO), respectively (Holton and Lindzen, 1972; Dunkerton, 1997; Baldwin et al., 2001), although the momentum transported by the MRG waves needs to be further quantified (Randel et al., 1990; Kim and Chun, 2015a).
Investigation of the distribution and variability of large-scale equatorial waves requires datasets with global coverage, and global (re)analyses are extremely useful datasets for this purpose. A reanalysis is a product of a data assimilation system which reconciles the observed atmospheric states from many kinds of measurements with the atmospheric governing equations resolved by a numerical prediction model. Reanalysis products depend on the assimilation method and prediction (“first-guess”) model, especially in the stratosphere where the assimilated fields are less constrained by the observations due to less density of observations when compared to the troposphere. Around the TTL, there exist abrupt vertical changes in the temperature and stability, which greatly modify characteristics of the equatorial waves, particularly their vertical wavelengths and amplitudes (e.g., Randel and Wu, 2005; Ryu et al., 2011). Representation of the TTL in reanalyses might be sensitive to the vertical resolution of the prediction model and assimilation techniques used (see Birner et al., 2006, for a case of the extratropical tropopause). Therefore, it is important to identify the difference/spread among various reanalysis products in their representation of the equatorial waves in the TTL and stratosphere. For example, equatorial wave activity in the TTL during 1990–1999 was compared using seven reanalyses by Fujiwara et al. (2012), and significant differences between the reanalyses were found.
In contrast to analyses, which are made using operationally changing, state-of-the-art versions of the prediction model and assimilation system, reanalyses are derived using fixed versions of the data assimilation system and first-guess models for the whole period of the product. This helps to generate a temporally homogeneous product, which benefits studies of long-term changes in meteorological variables. However, reanalyses also have a potential for inhomogeneities or discontinuities arising from introduction of new observational data into the assimilation. Examples include the introduction of radiance/temperature profiles derived from the Television Infrared Observation Satellite (TIROS) Operational Vertical Sounder (TOVS) suite (Smith et al., 1979) around 1978 and those from the Advanced TOVS (ATOVS) suite around 1998. While these measurements have improved the quality of reanalyses, it has been reported that the transition from the TOVS to ATOVS suites induced temporal discontinuities in assimilated variables such as upper-stratospheric global-mean temperature (Onogi et al., 2007; Simmons et al., 2014) and equatorial stratospheric mean wind and temperature (Kawatani et al., 2016).
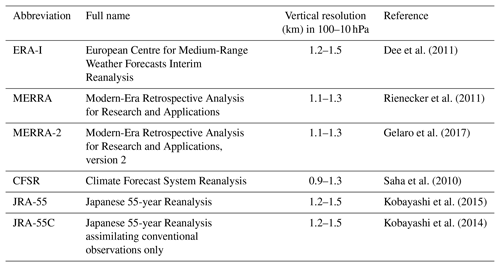
Dee et al. (2011)Rienecker et al. (2011)Gelaro et al. (2017)Saha et al. (2010)Kobayashi et al. (2015)Kobayashi et al. (2014)Table 1Reanalyses used in this study.
MERRA and MERRA-2 each provide two sets of products called ANA (analysis state) and ASM (assimilated state) (see Bloom et al., 1996, for the details), and the latter is used here.
To the best of our knowledge, impacts of such satellite transitions in reanalyses have so far not been studied in the context of equatorial waves. It is likely more difficult to identify discontinuities or inhomogeneities in wave fields which, by definition, contain smaller-scale variations in space and time than mean fields. Recently, a pair of reanalyses have been identically produced using a single assimilation system, with the exception that the satellite data are assimilated in one (JRA-55) but not in the other (JRA-55C; see Table 1 for the abbreviations and references). These datasets can allow us to identify the impact of satellite data in that assimilation system and, in particular, to help further distinguish the impact of the TOVS–ATOVS transition.
In this study, we investigate the characteristics of equatorial Kelvin and MRG waves in the TTL and stratosphere, and how they differ between recent reanalyses for the period of 1981–2010 (Sect. 3.1). Spatial distributions and patterns of the waves in the reanalyses are presented in Sect. 3.2. In Sect. 3.3, long-term changes in equatorial wave amplitudes are compared among the reanalyses and, based on the comparison between JRA-55 and JRA-55C, the effects of the satellite data on the assimilated waves are discussed. In addition, spectra of the Eliassen–Palm (EP) flux and its divergence, a measure of wave–mean flow interaction, are presented to compare the equatorial wave forcing of the QBO estimated from different reanalyses (Sect. 3.4). Among the results presented in Sect. 3.1, we identify a wave signal that has not been dealt with in the literature before, found at 20 hPa along with the well-documented equatorial waves in all the reanalyses studied. This wave spectrum is further discussed in Sect. 4. A summary of the results is included in Sect. 5.
We examine six reanalyses: ERA-I, MERRA, MERRA-2, CFSR, JRA-55, and JRA-55C (see Table 1 for their full names, vertical resolutions in the lower stratosphere, and key citations). The horizontal and vertical winds, temperature, and geopotential in the TTL and stratosphere for the period of 1981–2010 are used. The data we use are stored at 3 h intervals for MERRA and MERRA-2 and 6 h intervals for the others. The results do not significantly change if we use 6 h subsampled time series for MERRA and MERRA-2 (not shown) as we analyze equatorial waves with periods longer than 2 d. Both pressure-level datasets, which are interpolated to standard levels (SLs, e.g., 100 hPa), and model-level (ML) datasets are used for each reanalysis, except for MERRA of which ML data are not available. At 100 hPa and above in the tropics, pressure variations on a model level are negligibly small or absent in all of the reanalyses used in the present study (see the Supplement to Fujiwara et al., 2017). Therefore, the model levels can be regarded as being at nearly constant pressure levels, which allows us to simply perform spectral calculations on horizontal planes without the need to introduce vertical interpolation. For spectral shapes and spatial distributions of Kelvin and MRG waves, the results were very similar between SL and ML datasets (not shown), whereas wave amplitudes differ significantly, as will be seen in Fig. 8. Therefore, only the SL results are presented in Sect. 3.1 and 3.2, and the ML results (or both) are presented for quantitative analysis of wave variances and EP flux profiles in Sect. 3.3 and 3.4.
Zonal wavenumber–frequency (k–ω) spectra are calculated monthly at each latitude and height for each of the symmetric and antisymmetric components of variables with respect to the Equator. To obtain the monthly spectra, we use a 90 d time window centered on the target month. The window function is defined as C for the central 30 d and Csin (πt∕60) and Ccos (πt∕60) for the first and last 30 d, respectively, where t is the time (in days) relative to the first day of each 30 d segment and the normalization constant . The window function is determined such that for a long-term mean, the integral of the power spectrum equals the variance of the original variable. The spectra are calculated using the Fourier transform after removal of zonal mean and application of the time window, and they are averaged over the latitude range 15∘ N–15∘ S. The spectra are plotted in a variance-preserving form using base-10 logarithm axes in frequency and wavenumber.
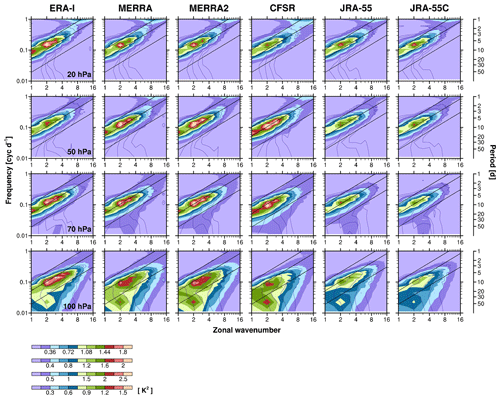
Figure 1Zonal wavenumber–frequency power spectra of the symmetric component of temperature at 100, 70, 50, and 20 hPa (from bottom to top) from the standard-level datasets of six reanalyses (ERA-I, MERRA, MERRA-2, CFSR, JRA-55, and JRA-55C: from left to right), averaged over 15∘ N–15∘ S in 1981–2010. The power spectra are presented in the variance-preserving form with log-scale axes. The Kelvin wave dispersion curves are indicated by black diagonal lines for the equivalent depths (h) of 8, 60, and 240 m. The ratio of the spectral power to that of the background spectrum is indicated by thin purple contours for the values of 1.5, 2, 3, and 5.
The use of a 90 d time window retains intraseasonal variations such as the Madden–Julian oscillation (MJO) partly in the spectra in the TTL at the lower-frequency range, as will be seen in Fig. 1. However, we will exclude these signals from our analysis and focus on signals with periods shorter than 20 d.
Following previous studies (Wheeler and Kiladis, 1999; Hendon and Wheeler, 2008; Fujiwara et al., 2012), the background spectra are obtained using the 1-2-1 filter repeatedly in wavenumber and frequency for each reanalysis. In this study, common background spectra for symmetric and antisymmetric components are obtained by averaging spectra of the two components before applying the filter. The filter is applied to the logarithm of the power spectrum; the number of passes is 23 for zonal wavenumber and 7 for frequency (Fujiwara et al., 2012).
k–ω spectra of the EP flux are also calculated monthly for symmetric and antisymmetric modes (Sect. 3.4). The EP flux formulation defined with the transformed Eulerian mean of the primitive equations is used (Andrews et al., 1987):
where
Here, u, v, w, θ, and ζa are the zonal, meridional, and vertical winds, potential temperature, and absolute vorticity, respectively; , where p and g are the pressure and gravitational acceleration, respectively, and H=6.6 km. The overbar and prime denote the zonal average and the perturbation from the average, respectively. The EP flux spectra for symmetric (antisymmetric) modes are obtained using uS, θS, wS, and vA (uA, θA, wA, and vS), where the subscripts S and A denote the symmetric and antisymmetric components of each variable, respectively. The flux terms are calculated via co-spectra (e.g., for the term for symmetric modes, where the hat indicates the complex Fourier coefficients of the variables, and the asterisk the complex conjugate). The same window function as the above is applied to all perturbation variables before calculating co-spectra. The terms A1 and A2 are averaged for the target month to be multiplied by the co-spectra. The EP flux spectra are averaged over 5∘ N–5∘ S, considering the meridional structures of the Kelvin and MRG wave EP fluxes and their divergence. The EP flux divergence would be largely underestimated if a broader latitude band is used for averaging, in particular for MRG waves for which the EP flux divergence changes its sign around 5∘ (e.g., Kim and Chun, 2015b, their Fig. 9c; Garcia and Richter, 2019, their Fig. 9b and d).
The buoyancy frequency used to compute equivalent depths of the equatorial waves is set to 0.024 s−1 based on the climatological temperature profile of the tropical lower stratosphere (e.g., Grise et al., 2010).
3.1 Spectral characteristics
Figure 1 shows k–ω power spectra for the eastward-propagating symmetric component of temperature (TS) at 100, 70, 50, and 20 hPa from the SL datasets of the six reanalyses, averaged over the 30-year period (1981–2010). The major portion of the spectral power appears along the Kelvin wave dispersion curves (black diagonal lines) at all altitudes. The spectral characteristics are broadly similar among the reanalyses with peaks at k=2–3. The reanalyses commonly exhibit a gradual shift of the Kelvin wave spectrum to larger equivalent depths (h) with respect to the altitude: the majority of the spectral power appears at h<60 m at 100 hPa, at h∼60 m at 70 hPa, and at h=60–240 m above 70 hPa. There exist variations in the spectral width in h: for example, compared to the other reanalyses, CFSR shows broader spectra at small equivalent depths (h<60 m) consistently at 70–20 hPa, with peaks at slightly smaller equivalent depths (70–50 hPa). In addition to the Kelvin wave signal, at 100 hPa, another peak exists at k=2 in the low-frequency range (ω<0.04 cyc d−1). As mentioned in Sect. 2, this is likely related to the intraseasonal MJO (Hendon and Wheeler, 2008).
The relative magnitude of Kelvin wave spectral power between ERA-I, MERRA, MERRA-2, and CFSR varies with height (Fig. 1), while JRA-55 and JRA-55C show generally less power below 20 hPa compared to the other four datasets. Note that relatively small variances in JRA-55 and JRA-55C are found in the temperature field but not in the wind fields (see Fig. S1 in the Supplement). In Fig. 1, the ratio of the spectral power to the background spectrum is also shown (thin purple contours), which indicates statistical significance of the spectral signals. A ratio of 1.2 was deemed to be statistically significant at the 95 % level by Wheeler and Kiladis (1999), and for the majority portions of the Kelvin wave spectra in Fig. 1, the ratios are generally larger than 1.5 (i.e., 50 % larger than the background spectral power), conservatively implying that the spectral peaks are all statistically significant.
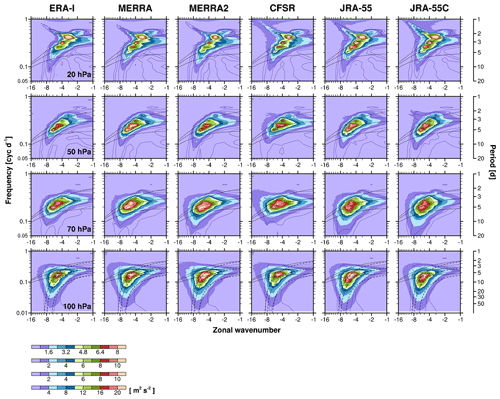
Figure 2The same as in Fig. 1 except for the spectra of the symmetric component of meridional wind. The mixed Rossby–gravity (MRG) wave dispersion curves for the windless background state are indicated by the dotted lines for h=8, 60, and 480 m. At 100 hPa, the dispersion curves for the background zonal wind of +10 m s−1 are also indicated by the long-dashed lines.
Figure 2 shows k–ω spectra for the westward-propagating symmetric component of v (vS) at 100, 70, 50, and 20 hPa. Note that the lower bound of the y axis at 100 hPa is different from that at the other levels, as the vS spectrum is much broader in frequency at 100 hPa. The 100 hPa spectrum has periods from around 2.5 d (0.4 cyc d−1) to longer than 30 d (0.033 cyc d−1), with a peak at , ω=0.1–0.2 cyc d−1 common to all of the reanalyses. In the upper troposphere, the background zonal wind near the Equator is westerly (easterly) in the western (eastern) hemisphere. MRG waves that are generated in the region of westerly (easterly) background flow can have relatively low (high) ground-based frequencies, which might result in the broad spectrum in frequency of vS at 100 hPa. The low-frequency portion of the wave spectrum at 100 hPa seems to roughly follow the MRG wave dispersion curves for a background wind (U) of +10 m s−1 (Fig. 2, long-dashed lines).
At 70 hPa, the low-frequency portion (<0.1 cyc d−1) of the spectrum is mostly filtered out, and commonly in all reanalyses, the peaks appear at , ω∼0.20 cyc d−1 and at , ω∼0.22–0.25 cyc d−1 (h∼60 m for both, assuming U=0) (Fig. 2). However, the lower bound in frequency of the spectral power is different between the reanalyses: JRA-55C, JRA-55, and MERRA-2 exhibit broader frequency spectra than the others. Above 70 hPa, another two local peaks appear in a higher-frequency region (, ω∼0.3 cyc d−1; , ω∼0.4 cyc d−1), in addition to the aforementioned peaks, and these peaks become primary at 20 hPa. At 50 hPa, the spectral shapes are generally similar among the reanalyses, although the spectral region where the majority of the power exists in CFSR is slightly shifted toward lower zonal wavenumbers when compared with the other reanalyses.
Figure 2 also exhibits a distinct feature in the vS spectra at 20 hPa, compared to the spectra at the lower altitudes: statistically significant power appears along the narrow spectral region that includes , ω∼0.5 cyc d−1 and extends into higher wavenumbers and frequencies in all of the reanalyses. Toward lower wavenumbers, it seems to merge into the aforementioned peak at , ω∼0.4 cyc d−1. The spectral power along this region is larger in JRA-55C, JRA-55, and CFSR than in the others. This portion of the spectrum is further examined in Sect. 4. As will be seen therein, the waves with this spectrum do not originate from below, and they appear with different timing and different characteristics from the lower-frequency upward-propagating MRG waves which dominate the vS spectra in the lower altitudes. In Sect. 3.2–3.4, we focus on the lower-frequency MRG waves filtered with a cut-off frequency of 0.33 cyc d−1 (period of 3 d).
The spectral shapes of Kelvin and MRG waves obtained from the ML datasets (not shown) are very similar to those from the SL datasets (Figs. 1 and 2) for each reanalysis, whereas their spectral power is larger by up to about 35 %, depending on the altitude and reanalysis. This will be further discussed in Sect. 3.3.
In the following sections, we define Kelvin waves as the symmetric mode with h=8–240 m, k=1–10, and periods of 2–20 d following Fujiwara et al. (2012), unless otherwise stated. These spectral components include a major portion of the Kelvin wave variances (Fig. 1), while excluding contributions of the other disturbances at low phase-speed ranges at 100 hPa (see also Fig. 9). The MRG waves are defined as the antisymmetric mode with h>8 m, , and periods of longer than 3 d, as previously mentioned, where h is for U=0. The perturbations filtered for these spectral components are denoted as, for example, TKelvin for the Kelvin wave temperature or vMRG for the MRG wave meridional wind.
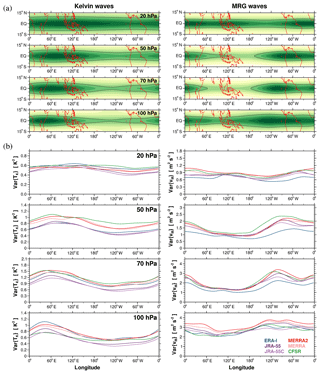
Figure 3Horizontal distributions of variances of (left) temperature for the Kelvin waves (TKelvin) and (right) meridional wind for the MRG waves (vMRG) at 100, 70, 50, and 20 hPa averaged for 1981–2010: (a) ensemble mean for ERA-I, MERRA-2, CFSR, and JRA-55, and (b) distributions at the Equator for each of the six reanalyses. In panel (a), the mean variances are normalized by their maximum value on each horizontal plane. The shading interval is 0.1, with the black contour indicating 0.5. See the text in Sect. 3.1 for the definitions of TKelvin and vMRG.
3.2 Spatial structure
To investigate the spatial distributions, the Kelvin and MRG signals are reconstructed in physical space by filtering their spectral components. Figure 3a shows the distributions of TKelvin and vMRG variances at 100, 70, 50, and 20 hPa during the period of 1981–2010, averaged for ERA-I, MERRA-2, CFSR, and JRA-55 (the reanalyses that assimilate satellite data are included as the ensemble members, but MERRA is excluded since it exhibits very similar spatial distributions to MERRA-2, as will be seen in Fig. 3b). The ensemble-mean variances are normalized by their maximum values on each horizontal plane. Both the Kelvin and MRG wave variances are confined near the Equator, and the locations of their maxima slant eastward in the vertical, consistent with the equatorial wave theory. Note that, while the phase of MRG waves propagates westward, their wave packet travels eastward when the background flow is westerly or weak easterly which is a preferred condition for MRG wave propagation in the stratosphere. The maxima of variances for the Kelvin (MRG) waves are located in the eastern (western) hemisphere in the lower stratosphere: 70 and 50 hPa, consistent with previous observational studies (Alexander et al., 2008; Yang et al., 2012; Kiladis et al., 2016). At 20 hPa, the Kelvin and MRG waves show rather broad distributions in longitude. The distributions of the wave variances at 100 hPa are closely related to those of background zonal wind in the upper troposphere (Yang et al., 2012; Flannaghan and Fueglistaler, 2013). The easterly (westerly) upper tropospheric wind in the eastern (western) hemisphere allows Kelvin (MRG) waves to more readily propagate vertically, resulting in the hemispheric difference in the wave variances. In addition, the MRG wave variances at 100 hPa are distributed quite broadly in longitude (Fig. 3a). Yang et al. (2012) showed that during the northern winter the MRG wave variances in the upper troposphere are much larger in the western hemisphere, with peaks at about 140 and 30∘ W, than in the eastern hemisphere, whereas during the northern summer, the variance distribution becomes broad, stretching to the western Pacific (see their Fig. 6).
Figure 3b shows the wave variances at the Equator in each of the six reanalyses. The longitudinal variations of the Kelvin wave variances seem broadly similar among the reanalyses, with peaks at approximately 45∘ E at 100 hPa and at 75–110∘ E at 50 hPa, although the Kelvin waves in CFSR show much smaller longitudinal variations than those in the other reanalyses at 100 and 50 hPa. The MRG waves have maximum variances in the eastern Pacific and South America at 70 and 50 hPa, and these maxima are roughly twice the minima over the Maritime Continent and western Pacific, common to all of the reanalyses. However, at 50 hPa, detailed distributions in the eastern hemisphere show some differences among the reanalyses: the peak in ERA-I is eastward of that in the others (e.g., 35–45∘ eastward of CFSR, JRA-55, and JRA-55C), and the variance in CFSR seems to extend further to the west (∼150∘ W). Differences between JRA-55 and JRA-55C appear over the Indian Ocean for Kelvin waves and the eastern Pacific for both waves, whereas the differences are very small on the Maritime Continent and western Pacific at all altitudes. These could be explained in part by relatively large numbers of radiosonde observations near the Maritime Continent compared to the other regions around the Equator in these two reanalyses (Fig. 5 in Kawatani et al., 2016; Fig. 2.8c and 2.9c in Wright et al. (2019)).
The locations of the wave variances vary with respect to the QBO winds in the stratosphere (not shown). For example, MRG wave variances averaged for the 50 hPa easterly QBO are located to the west of those for the westerly QBO. However, the MRG wave variances are much smaller in the easterly QBO phases, and their contribution to the climatological-mean variances shown in Fig. 3 is relatively small. Therefore, the results in Fig. 3 are more representative of the westerly QBO phases for MRG waves and, similarly, easterly phases for Kelvin waves.
The currently used filters for the MRG waves exclude the low-frequency perturbations (<0.1 cyc d−1) at 100 hPa revealed in Fig. 2, of which the spectrum follows the dispersion curves for U∼10 m s−1. An additional calculation, the same as with Fig. 3, is performed but for the 100 hPa low-frequency components of vS using the filters for cyc d−1 and (Fig. S2). It is observed in all the reanalyses that the low-frequency perturbations are located mostly in the western hemisphere where westerlies exist (over the eastern Pacific and Atlantic), consistent with the Doppler-shifted dispersion curves discussed in Fig. 2.
To further investigate the spatial structures of the Kelvin and MRG waves, including the circulation patterns and horizontal scales of representative wave modes in each reanalysis, an empirical orthogonal function (EOF) analysis is used following the technique outlined in Kiladis et al. (2016). In that study, EOFs were calculated from the covariance matrix of a 2–6 d filtered meridional wind in 20∘ N–20∘ S from ERA-I data to isolate MRG waves. The filter band was based on the well-documented strong spectral peak in the equatorial meridional wind centered at around the 4.5 d period (Fig. 2). Dynamical fields associated with each EOF were obtained by projecting unfiltered ERA-I data at each grid point onto the associated principal component (PC) time series.
Here, we use data interpolated to 2.5∘ resolution for the six reanalyses considered. A similar technique as in Kiladis et al. (2016) is used to obtain the statistical structures of the equatorial Kelvin waves, except that a 2–25 d eastward-only filter band is applied to the equatorial zonal wind based on the spectral peaks in Fig. 1. The results are very robust to changes in the filtering, as long as the filter band contains the spectral peaks shown in Figs. 1 and 2, and to changes in latitudinal extent of the EOF basis.
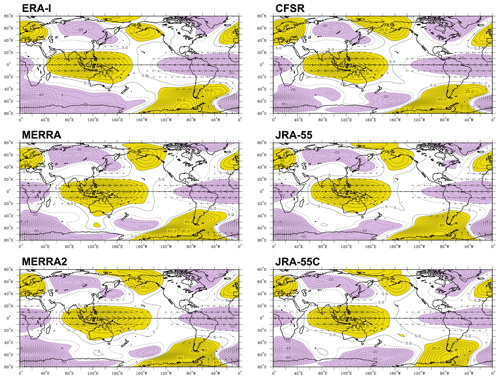
Figure 4Horizontal-wind (arrow) and geopotential perturbations (shading) projected onto the principle component time series of the first EOF modes for Kelvin waves at 50 hPa in each reanalysis. The EOFs for Kelvin waves are calculated using 2–25 d filtered eastward-propagating zonal winds (see the text). The winds are shown at the locations where they are statistically significant.
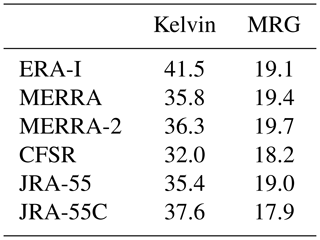
In all cases, EOF “pairs” are obtained with respective PC time series that correlate at better than 0.96 (with time lag), which together represent the propagating pattern of Kelvin or MRG waves. Thus, each mode can be represented by either EOF pattern and its associated PC. Figure 4 shows the projected structures of the leading modes (EOF 1) of 50 hPa Kelvin waves from the six reanalyses for the period of 1981–2010. Wind vectors are shown at the locations where they are statistically significant, taking into account temporal and spatial autocorrelation. In all cases, zonal wavenumber 1 structures are obtained as the leading modes in the tropics, with zonal wind perturbations in phase with geopotential, as expected from theory. Especially in the tropics, remarkably similar patterns are found in all of the reanalyses. The wind and geopotential perturbations exhibit much larger amplitudes in the eastern hemisphere than in the western hemisphere, consistent with the result in Fig. 3. Higher-order Kelvin EOF pairs represent integer zonal wavenumber structures, with k=2 Kelvin structures comprising the second EOF pair (EOFs 3 and 4). The second EOF pairs also show reasonable agreement among the reanalyses (not shown). The k=1 patterns shown in Fig. 4 account for the largest portion of total variance in the equatorial 2–25 d eastward zonal wind in each reanalysis, which amounts to a maximum of 42 % in the case of ERA-I and somewhat smaller amounts in the other reanalyses (Table 2).
Table 2Percentage of variance explained by the leading EOF pairs representing Kelvin and MRG waves for each reanalysis.
Lag regressions based on the PC time series show the eastward propagation of the Kelvin wave signals at a mean phase speed of around 35 m s−1 (not shown), which is rather faster than the 20–30 m s−1 found in previous studies, although these phase speeds are highly dependent on the state of the QBO (e.g., Randel and Wu, 2005; Ern et al., 2008; Lott et al., 2009, 2014). While these features will be explored in further detail in a future study, the main point here is that the various reanalyses appear to be quite suitable for studying the mean statistical structure of these waves, as well as their variability.
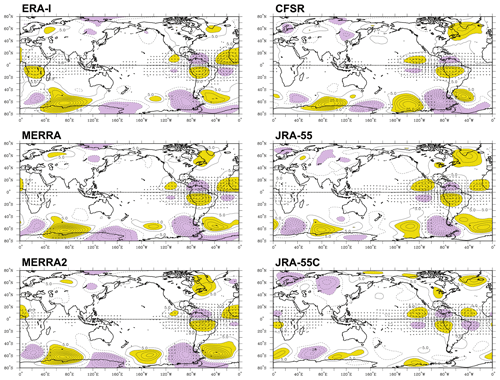
Figure 5The same as in Fig. 4 except for MRG waves. The EOFs for MRG waves are calculated using 2–6 d filtered meridional winds.
The situation for the MRG wave signals is rather different (Fig. 5). The leading MRG EOFs represent localized wave packets that are confined over the eastern Pacific to Atlantic sector, as expected from the location of the variance peaks in Fig. 3. The EOF patterns have classical structures of equatorial gyres and off-equatorial antisymmetric geopotential perturbations as predicted by Matsuno (1966). The reanalyses each represent structurally very similar MRG wave patterns, except for CFSR which has a zonally broader signal (i.e., longer wavelengths), consistent with the spectra shown in Fig. 2. In addition, the MRG wave patterns in JRA-55, JRA-55C, and CFSR are displaced somewhat to the west of the other reanalyses, again reflecting their variance distributions shown in Fig. 3b. The higher-mode EOF pairs of MRG waves (not shown) have wave structures over the Indian and Pacific oceans, with good agreement among the reanalyses for up to the fourth mode pairs.
Kelvin and MRG signals at other levels from 70 to 10 hPa are broadly similar to those shown here, although the structures change considerably at 100 hPa (not shown). In summary, there is reasonable agreement between the reanalyses in their statistical representation of Kelvin and MRG wave structures, at least for the leading modes.
3.3 Long-term change and satellite effects
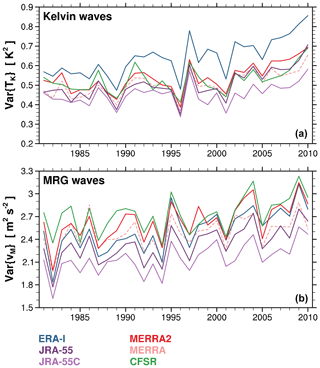
In this section, we analyze long-term variations in the Kelvin and MRG wave activity and discuss the impact of satellite data upon the assimilated wave activity based on the comparison of JRA-55 and JRA-55C. Figure 6 shows annual-mean time series of 100 hPa TKelvin and vMRG variances, as defined in Sect. 3.1. The results from the ML datasets are presented (solid lines), except for MERRA for which the SL datasets are used (dashed lines) due to the lack of ML data. The variance of TKelvin in ERA-I fluctuates between about 0.5 and 0.85 K2 with an increasing trend, whereas that in JRA-55C fluctuates between ∼0.35 and 0.58 K2 without such an obvious trend. Despite this difference, much of the interannual variability in the Kelvin wave activity is reflected in both time series, with a Pearson linear correlation of 0.85 (0.88 after trend removal) between the two. Similar correlations are obtained between the other series, with the TKelvin variances ranging between those in ERA-I and JRA-55C. By comparing JRA-55 and JRA-55C, it appears that assimilation of satellite data leads to an increase in the Kelvin wave temperature variance, as also found in the previous section (Fig. 3b).
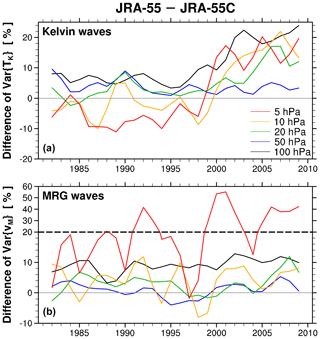
Figure 7Differences in the annual-mean variances of (a) TKelvin and (b) vMRG over 15∘ N–15∘ S between JRA-55 and JRA-55C, relative to the 30-year mean variances in JRA-55C, at various altitudes. The 1-2-1 smoothing is applied to the differences to filter out the interannual fluctuations by the QBO. The results are obtained from the model-level datasets.
The difference in the variance between JRA-55 and JRA-55C is further investigated in Fig. 7, which presents the time series of the annually averaged difference at altitudes from 100 to 5 hPa. Because the wave variance in the stratosphere is strongly dependent on the QBO (e.g., Yang et al., 2012), 1-2-1 smoothing is applied to the annual time series to filter out the quasi-biennial fluctuations and focus on the longer-term variations. It is evident that the difference (JRA-55 minus JRA-55C) in the TKelvin variance is generally positive from 100 to 20 hPa during the 30-year period, indicating the enhancement of the Kelvin wave amplitude by assimilation of satellite data in JRA-55. In addition, it is noteworthy that at 100 hPa, the difference is systematically larger from around 2000, compared to that before late 1990s: it is roughly 6 % (up to ∼8 %) in the years before 1998, whereas it increases to ∼10 % in 1998–2000 and becomes ∼20 % afterward. A similar systematic change of the difference in the TKelvin variance is even more evident in the upper stratosphere: at 10 and 5 hPa (Fig. 7) and above (not shown), where the difference is mostly negative until 1998 and becomes positive after 1999. Such changes are not found at 50 hPa.
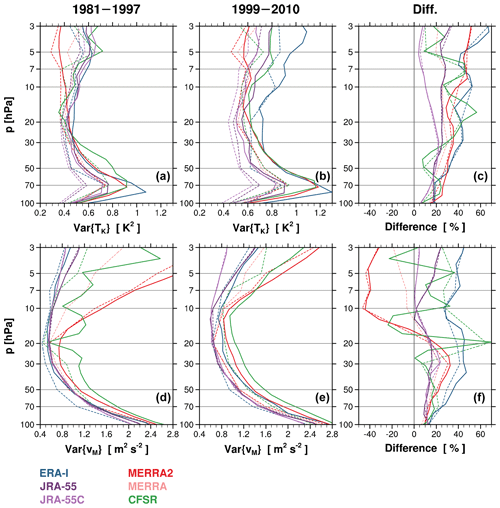
Figure 8Variance profiles of (a, b, c) TKelvin and (d, e, f) vMRG averaged over the periods of (a, d) 1981–1997 and (b, e) 1999–2010, and (c, f) their differences (1999–2010 minus 1981–1997) relative to the 30-year average (1981–2010). The dashed and solid lines indicate the results from the standard-level and model-level datasets, respectively.
The systematic change in the impact of satellite data assimilation on the Kelvin wave amplitude in JRA-55 around 1998 might be due to the TOVS–ATOVS transition, given the timing of the change (see Fig. 8 in Fujiwara et al., 2017, for the timelines of satellite data used in JRA-55 and other reanalyses). The Advanced Microwave Sounding Unit A (AMSU-A) instruments in the ATOVS suite were introduced in 1998. Compared to the Stratospheric Sounding Unit (SSU) instruments in the TOVS suite, the AMSU-A observations have better vertical coverage with a higher vertical resolution (see Fig. 7 in Fujiwara et al., 2017, for the vertical weighting functions of the SSU and AMSU-A measurements). The vertical weighting functions of the two suggest that the AMSU-A instruments could be advantageous over the SSU, particularly at an altitude of ∼100 hPa which the latter does not cover. This may explain the systematic change found at 100 hPa around 1998 (Fig. 7). The higher vertical resolution of the AMSU-A instruments is expected to mostly benefit the upper stratosphere where radiosonde sounding observations do not reach (i.e., above ∼10 hPa). This is consistent with the observed systematic change being most prominent in the upper stratosphere. In addition to the TOVS–ATOVS transition, there is also a possibility that the Global Navigation Satellite System Radio Occultation (GNSS-RO) has been influencing the assimilated waves in JRA-55 since 2006 (Fig. 10 in Fujiwara et al., 2017), although this cannot be identified by the current analysis.
Recalling that JRA-55C does not exhibit a long-term trend in Kelvin wave activity at 100 hPa (Fig. 6), the trend shown in JRA-55 is probably not an actual change in the true atmosphere but instead an artifact arising due to the satellite transition. The change in the 100 hPa TKelvin variance around 1998 is 17 % in JRA-55 when it is measured by the difference between the variances averaged for the two periods before and after 1998, i.e., 1981–1997 (P1 hereafter) and 1999–2010 (P2), relative to the 30-year mean variance. The changes in the other reanalyses are comparable to or smaller than that in JRA-55 (e.g., 19 % in ERA-I, which is the largest value). This suggests that the long-term changes in the 100 hPa Kelvin wave activity shown in those reanalyses also could result largely from the satellite transition.
The variance of vMRG exhibits generally similar interannual variations at 100 hPa between all of the reanalyses (Fig. 6), while the magnitudes of the variance are different. The vMRG variance has an increasing long-term trend from the early 1990s, even in JRA-55C. The vMRG variance at 100 hPa in JRA-55 is always larger than that in JRA-55C by roughly 6 %–12 % (Figs. 6 and 7), reflecting the impact of satellite data on the assimilated MRG waves. In addition, the assimilation of satellite data increases the analyzed MRG wave activity at 5 hPa in JRA-55 (Fig. 7). This increase is up to ∼55 %, and it becomes even larger at higher altitudes (see Fig. 8). Notable differences between P1 and P2 in the satellite impact on the assimilated MRG wave activity are not found below 5 hPa (Fig. 7). At 5 hPa, the impact is significantly larger in P2 than in P1 (note that two different scales are used in the y axis in the bottom panel of Fig. 7, below and above 20 %, separated by the dashed horizontal line).
Figure 8 presents the vertical profiles of TKelvin and vMRG variances averaged for P1 and P2 along with the differences between the two periods. In the ML results, the TKelvin variance is maximized at approximately 80 hPa in ERA-I and at 70 hPa in the others for both periods. These peak altitudes are generally consistent with that obtained using GNSS-RO data in 2007–2014 by Scherllin-Pirscher et al. (2017, Fig. 6): 18 km (75–80 hPa), considering vertical grid spacings of the reanalyses. The TKelvin variance decreases with height from these levels to ∼30 hPa and gradually increases from ∼20 hPa in both periods in all the reanalyses, except in MERRA-2 during P1. Further examination indicates that sometimes the temperature seems not to be properly assimilated in the upper stratosphere during P1 in MERRA-2 (Fig. S3; note the lack of Kelvin wave peaks in 1984, 1989, and 1991), which may result in the decrease above ∼20 hPa in P1 in MERRA-2. It has previously been reported that the monthly mean zonal wind at 10 hPa in MERRA-2 shows significant differences from observations, in particular with larger annual/semiannual oscillations, until the mid-1990s (Coy et al., 2016; Kawatani et al., 2016), which is perhaps partly related to the underrepresentation of the Kelvin wave temperature shown in Fig. S3. Errors in a mean state of assimilated fields can cause degradation of any variables describing waves during the first-guess model integration, which in turn degrade the assimilated fields 3 or 6 h later. In P2, the TKelvin variance at 70–30 hPa has similar magnitudes between ERA-I, MERRA-2, and CFSR, while JRA-55 exhibits a relatively smaller variance than these reanalyses, as is also evident in Fig. 1. In the upper stratosphere, the variance is notably larger in ERA-I in P2 than in the others (also see Fig. S3).
The difference in the TKelvin variance between P1 and P2 is positive in the whole stratosphere in all of the reanalyses (Fig. 8). In JRA-55C, the difference is small at 100 hPa (∼6 %), as already discussed (Fig. 6), and above 10 hPa (4 %–8 %), although it reaches ∼20 % at 50–20 hPa. Given the small difference in Kelvin wave activity at ∼100 hPa, the increase in the activity at 50–20 hPa could result from interaction with the QBO which itself has variability in its morphology. However, since only five (seven) QBO cycles are included in P2 (P1), further investigation of the long-term change associated with the QBO might be less meaningful in a statistical sense. Another possible reason could be the increased number of radiosonde observations around 30 hPa with time (see Fig. 15 in Kawatani et al., 2016). In JRA-55, the difference is large in the upper stratosphere (∼25 % or larger), and it is even larger in ERA-I, MERRA-2, and CFSR. Similarly to the case of JRA-55, the large increase in Kelvin wave activity in the middle and upper stratosphere in the other reanalyses could also be in large part due to the transition of satellite instruments. From Fig. S3, it is evident that the difference in the Kelvin wave variances at 10 hPa between ERA-I and the others increases abruptly around 2000, which may support such an impact of the satellite instrument change in ERA-I.
In all the reanalyses, the vMRG variance decreases with height below ∼20 hPa and increases above ∼10 hPa (Fig. 8). In both periods, MERRA-2 and CFSR exhibit larger variances than the others, particularly in the upper stratosphere. In P1, it is seen in the upper stratosphere that the vMRG variance in the ML result of CFSR varies less smoothly in the vertical and that the variance in MERRA-2 is about 2–3 times larger than that in the others. These features are still present to a lesser extent in P2. Examination of time series of the vMRG variance (Fig. S3) shows that some unexpected peaks appear in P1 in MERRA-2 with exceptionally large magnitudes even during the easterly QBO phase, which are primarily responsible for the large value of the vMRG variance in P1 shown in Fig. 8. The unexpected peaks disappear suddenly starting in 1999 (Fig. S3), likely emphasizing the impact of the AMSU-A observations on the assimilated wave activity in MERRA-2. Regarding the vertical fluctuations exhibited in CFSR, the reason for this is unknown. The profiles of the difference between P1 and P2 may imply that above 10 hPa, the large increase in the vMRG variance in JRA-55 (10 %–25 %) and ERA-I (∼40 %), compared to the small increase in JRA-55C (∼5 %), is probably in large part due to the satellite transition.
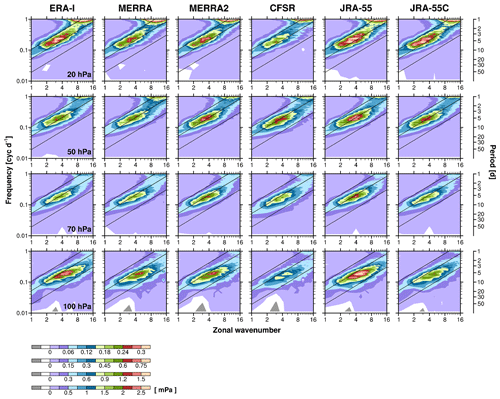
Figure 9Zonal wavenumber–frequency spectra of the vertical EP flux, multiplied by −1 (−Fz), for symmetric modes at 100, 70, 50, and 20 hPa (from bottom to top) from the standard-level datasets of six reanalyses, averaged over 5∘ N–5∘ S in 1981–2010. The Kelvin wave dispersion curves are indicated by black diagonal lines for h=8, 60, and 240 m.
Table 3Differences in the mean variances over 1981–2010 between the ML and SL results, relative to the ML results (%), for the (left) Kelvin wave temperature and (right) MRG wave meridional wind.
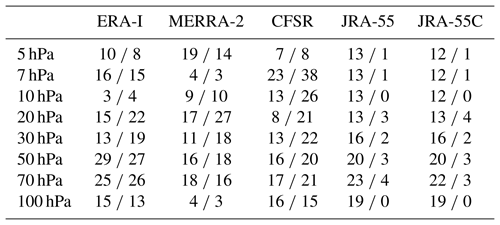
In each reanalysis, the variances obtained from the SL datasets are smaller than those from the ML datasets in both periods (Fig. 8) by 3 %–29 % (0 %–38 %) for Kelvin (MRG) waves depending on the altitudes and reanalyses. The differences in the variances between the ML and SL results (ML minus SL) normalized by the variances in the ML results at each altitude are reported in Table 3. The smaller amplitudes of the waves in the SL datasets compared to those in the ML datasets result from vertical interpolation of reanalysis output variables, which inevitably damps wave perturbations in the standard-level products of reanalyses. The damping by the interpolation is more significant for waves with smaller vertical wavelengths (e.g., Kim and Alexander, 2013; Kim and Chun, 2015a). In addition, for a given pressure level, the damping of waves in the SL datasets also depends on the distance between the given level and its adjacent model level. That is, the interpolation effect must be less if a model level is very close to the given pressure level. For example, the distance between 100 hPa and its adjacent model level in MERRA-2 is very small (<50 m), and thus the difference between the SL and ML results of MERRA-2 is only 3 %–4 % at 100 hPa (Table 3). The same (opposite) is true for the 10 hPa (50 hPa) in ERA-I, with a small (large) difference at that level. In JRA-55 and JRA-55C, the difference in the vMRG variance between the ML and SL results is less than 5 % at all levels, implying that the ML fields of these two reanalyses contain less of the MRG wave perturbations with small vertical wavelengths (∼2Δz–4Δz, where Δz is the vertical grid spacings of their model), compared to the other reanalyses.
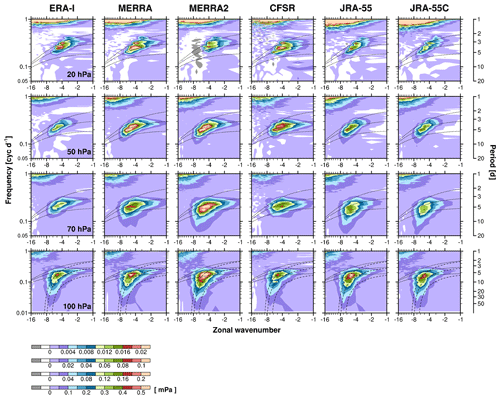
Figure 10The same as in Fig. 9 but for Fz of antisymmetric modes. The MRG wave dispersion curves for the windless background state are indicated by the dotted lines for h=8, 60, and 480 m. At 100 hPa, the dispersion curves for the background zonal wind of +10 m s−1 are also indicated by the long-dashed lines.
3.4 EP flux
In this section, we compare the vertical EP flux (Fz) spectra and the wave forcing of the QBO calculated by the EP flux divergence among the reanalyses. As for the figures discussed in Sect. 3.1, we obtain k–ω spectra for each of the symmetric and antisymmetric modes but for Fz averaged over 5∘ N–5∘ S (Figs. 9 and 10, respectively; see Sect. 2 for justification of the narrowed latitude band). The spectral characteristics of Fz for the symmetric and antisymmetric modes are qualitatively similar to those of TS and vS, respectively, for each reanalysis. For the symmetric mode, the Fz spectra are aligned along the Kelvin wave dispersion curves with h values that are similar to those for TS, along with exhibiting a gradual shift of the spectra to the higher h with increasing altitudes (Figs. 1 and 9). On the other hand, the symmetric Fz and TS spectra differ in that the Fz (TS) spectra have peaks at k=3–5 (2–3) in all of the reanalysis and that the magnitudes of Fz in JRA-55 and JRA-55C are not smaller compared to those in the others as was the case for temperature (Fig. 1). As already mentioned, JRA-55 and JRA-55C have relatively weak Kelvin wave temperature amplitudes but not wind amplitudes (Fig. S1), and the major term of Fz for Kelvin waves is the vertical momentum flux (). The reason that the peak of Fz occurs at larger zonal wavenumbers than in the TS spectra is because the vertical wind perturbations tend to have large amplitudes at higher zonal wavenumbers: the ratio of vertical to horizontal wind amplitudes is proportional to k∕m (where m is the vertical wavenumber), as from the continuity equation. In the Kelvin wave dispersion relationship, k is independent of m, so that the ratio is proportional to k for given m.
For the antisymmetric mode, Fz has similar spectral shapes and roughly the same (k,ω) peaks as those of vS for each reanalysis below 20 hPa (Figs. 2 and 10). Consistent with the vS spectra, the frequency bounds of the Fz spectra at 70 hPa are quite a bit lower in JRA-55, JRA-55C, and MERRA-2 than in the other reanalyses. At 20 hPa, the Fz spectra differ from the vS spectra in that the relatively low-frequency and high-wavenumber (and thus low phase-speed) components are largely suppressed in the Fz spectra. Indeed, these low-frequency components are more emphasized in the meridional EP flux (Fϕ) spectra (Fig. S4), implying that the low-frequency MRG waves tend to propagate laterally rather than vertically. In addition, even negative Fz values appear in the 20 hPa spectra at k=6–7 in MERRA-2, while this feature is less clear in the other reanalyses. This is suggestive of coexistence of upward- and downward-propagating waves at this level which could be another reason for the small Fz in the low-frequency range.
The EP flux spectra are reconstructed as a function of phase speed to investigate the vertical propagation and dissipation of Kelvin and MRG waves during different QBO phases and to quantify the QBO forcing by those waves as well as the phase-speed ranges responsible for the forcing. For this, we construct bins of phase speeds (cj) with a width of 2 m s−1 (Δc) and integrate the k–ω spectral densities of Fϕ and Fz across the corresponding bins (i.e., , where ω is in cycles per second and a is the mean radius of the Earth).1 The EP flux divergence is also calculated in each bin. For each wave type, the same filters as described in Sect. 3.1 are used: h=8–240 m, k=1–10, and cyc d−1 for Kelvin waves and h>8 m, –10, and ω<0.33 cyc d−1 for MRG waves.
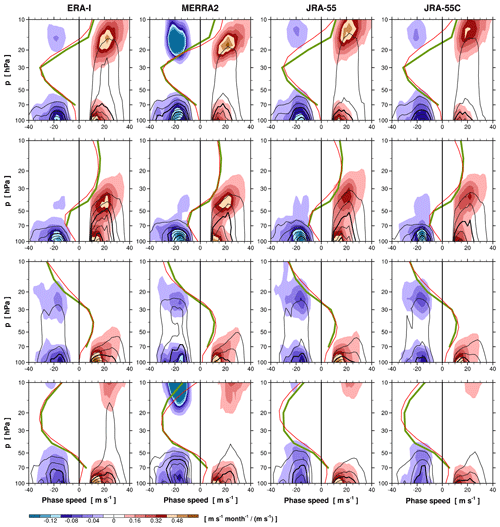
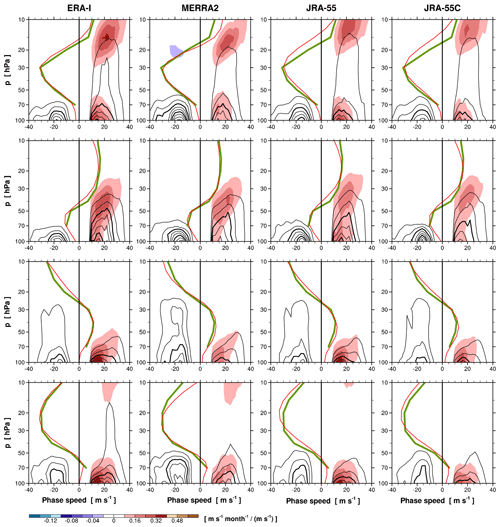
Figure 11Vertical profiles of phase-speed spectra of the EP flux divergence (shading) and vertical EP flux (black contour) averaged over 5∘ N–5∘ S for the Kelvin waves at c>0 and MRG waves at c<0, composited for the QBO phases of maximum westerly tendencies at 20 and 50 hPa (the first and second rows, respectively) and easterly tendencies at 20 and 50 hPa (the third and last rows, respectively) within the period of 1981–2010, from the model-level datasets of ERA-I, MERRA-2, JRA-55, and JRA-55C. The zonal-wind profiles for those composites are also indicated using each reanalysis (thin red lines) and radiosonde observations (thick green lines; see the text for the composite method). The contour intervals of the EP flux are 0.008 and 0.0003 mPa ∕ (m s−1) for the Kelvin and MRG waves, respectively, and every third contour is distinguished by thicker lines. Note that the contour interval of the EP flux divergence for the Kelvin waves is 4 times larger than that for the MRG waves.
Figure 11 shows vertical profiles of 5∘ N–5∘ S averaged EP flux divergence and Fz as a function of phase speed, for Kelvin and MRG waves at c>0 and c<0, respectively, composited for four different phases of the QBO. The composite is made by selecting 1 month for each QBO cycle when the zonal wind tendency is largest at a given altitude and then averaging over the 13 cycles available. The observed monthly mean near-Equator wind profiles compiled by the Freie Universität Berlin (FUB) are used to select the months. The four composites presented in Fig. 11 are for the months of maximum westerly and easterly tendencies at 20 and 50 hPa. The composite averages of the FUB wind are also plotted in Fig. 11 (thick green lines) as well as those of each reanalysis wind (thin red lines). The results are generated using the ML datasets of the four reanalyses available for EP flux calculation (ERA-I, MERRA-2, JRA-55, and JRA-55C), since the EP flux could be largely underestimated when using the SL datasets. Furthermore, the height dependence of the amplitude damping, as reported in Table 3, could also affect the estimation of the vertical divergence of EP flux (see Fig. 3 in Kim and Chun, 2015a, for a large difference in the EP flux divergence between ML and SL datasets of ERA-I).
The EP flux divergence of the Kelvin waves is found to be quite different between reanalyses not only in magnitude but also in its peak altitude. At the maximum westerly tendency phase at 20 hPa (Fig. 11, the first row), the vertical EP flux is notably the largest in ERA-I at ∼20 hPa. However, the EP flux divergence at this level is the largest in MERRA-2, implying that the assimilated wave fields exhibit the most severe dissipation in MERRA-2 among the reanalyses around this level. ERA-I and JRA-55 show the peaks of the EP flux divergence at ∼15 and 12 hPa, respectively. It is important to note that the easterly-to-westerly transition (i.e., zero wind) occurs at different altitudes between the reanalyses (Fig. 11, red lines; also refer to Fig. 16 in Kawatani et al. (2016), for different time evolutions of the phase transition) and that the maximum Kelvin wave forcing is found to occur at around the zero-wind altitudes in each reanalysis. These suggest that the mean wind in the assimilated field could affect the representation of wave behaviors in reanalyses in the shear zone. The phase speed at which the forcing occurs increases with altitudes from 10–30 m s−1 at 20 hPa to 15–40 m s−1 at 10 hPa but with large spread at 10 hPa among the reanalyses. The Kelvin wave forcing integrated for the phase speed has maxima of 9.2, 10.2, and 10.0 m s−1 month−1 in ERA-I, MERRA-2, and JRA-55, respectively. When the westerly tendency is maximized at 50 hPa (Fig. 11, the second row), the peak of the Kelvin wave forcing appears slightly below (above) 40 hPa in ERA-I and MERRA-2 (JRA-55). Similar to the 20 hPa transition phase, the vertical EP flux is the largest in ERA-I, while the EP flux divergence at ∼40 hPa is larger in MERRA-2 (8.6 m s−1 month−1), which may also be related to the different mean-wind profiles in the reanalyses. Note that the mean winds in ERA-I and JRA-55 have weaker shear at 40–50 hPa with weaker westerly magnitudes above 40 hPa compared to the observed winds (Fig. 11, thick green lines), and they might affect the wave dissipation rate in these reanalyses. At the other two phases of the QBO (Fig. 11, the third and last rows), the zonal wind is westerly at 70 hPa, causing less upward propagation of Kelvin waves in the lowermost stratosphere.
Figure 12 shows the vertical divergence of the EP flux, , as a function of phase speed, along with Fz as in Fig. 11. In the main regions of the Kelvin wave forcing during the westerly-shear phases (Fig. 12, the first and second rows), the vertical divergence of the EP flux for the Kelvin waves is roughly 50 %–75 % of the total divergence shown in Fig. 11. The vertical divergence is the largest in ERA-I among the reanalyses, whereas the total divergence of the EP flux is larger in MERRA-2 (Fig. 11). This indicates that the contribution of meridional flux divergence to the Kelvin wave forcing is relatively large in MERRA-2 (40 %–50 %, not shown) compared to that in the other reanalyses (25 %–45 %). The Kelvin wave flux tends to be slanted toward the Equator in westerly-shear winds (e.g., Plumb and Bell, 1982; Kim and Chun, 2015b). The larger wind shear in MERRA-2 is likely the cause for the larger contribution of meridional divergence of the flux.
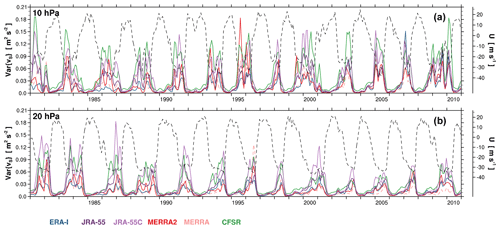
Figure 13Monthly time series of variances of the symmetric component of meridional wind at (a) 10 and (b) 20 hPa, filtered for cyc d−1 with and cyc d−1 with (see Fig. 2). The monthly zonal wind from radiosonde observations is also presented at each level (dashed black lines).
MRG waves dissipate largely in the lower stratosphere when the zonal wind is easterly at 70 hPa (Fig. 11, the first and second rows). The MRG wave forcing is about 2–3 m s−1 month−1 below 70 hPa in these QBO phases in the reanalyses. When the 20 hPa easterly tendency is at its maximum (Fig. 11, the third row), MRG waves propagate through the lower stratospheric westerlies and dissipate at around 30–20 hPa. The forcing by the MRG waves at these altitudes is largest in JRA-55 (∼1.6 m s−1 month−1), where it occurs at phase speeds between −10 and −30 m s−1. It is also found in Fig. 11 (the first and last rows) that the EP flux divergence of MRG waves exists in the westerly-shear zone at 10–20 hPa in MERRA-2 when the easterly jet is located at 20–40 hPa. This signal also exists in the other reanalyses but with much weaker magnitudes. The waves responsible for this signal seem not to originate from below, as the vertical EP flux from the lower altitudes is interrupted by the easterly winds. The phase speeds of the signal (around −20 m s−1) correspond to the spectral region where Fz is suppressed in Fig. 10 (but Fϕ is emphasized in Fig. S4) mentioned previously. The EP flux divergence in this region is about 3–4 m s−1 month−1 in MERRA-2, although it is uncertain to estimate because of the large discrepancy between MERRA-2 and the others and the larger westerly shear in MERRA-2 compared to the observed (Fig. 11). Previously, Maury and Lott (2014) also found that MRG waves with the phase speed of −19 m s−1 appear at 20 hPa when there exist easterlies (westerlies) at 50 hPa (20 hPa), using ERA-I. Recently, using a climate model, Garcia and Richter (2019) simulated MRG waves existing in a westerly-shear zone (see their Fig. 9b), which were generated locally by barotropic instability of the westerly QBO jet. These waves have a spectral peak at around k=7–8 and ω∼0.2 cyc d−1 (see their Fig. 8a) which is similar to that detected in MERRA-2 (Fig. S4). The simulated MRG waves induced westward forcing of 7.5–15 m s−1 month−1.
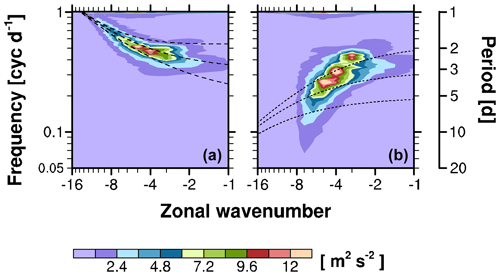
Figure 14The same as in the rightmost panel of the first row in Fig. 2 (JRA-55C, at 20 hPa) except for the averages over the months when (a) the radiosonde-observed zonal wind m s−1 and (b) m s−1. The dashed lines in panel (a) indicate the MRG wave dispersion curves for h=8, 60, and 480 m for the background wind of −30 m s−1, and the dotted lines in panel (b) indicate those for the windless background state.
In Fig. 12, it is seen that for MRG waves, the contribution of vertical divergence of the EP flux to the total divergence is very small everywhere (∼10 %). In addition, the EP flux divergence and Fz for each of the composited 13 QBO cycles, as well as the individual profiles of the mean winds, are included in the Supplement (Fig. S5). While there are substantial cycle-to-cycle variations, the overall structures of the EP flux and its divergence for all cases are generally similar to those of the composite averages shown in Fig. 11.
As mentioned in the introduction, the momentum budget of the QBO is currently not fully constrained by observations, and it is believed to be essential for modeling the QBO. The different altitudes of Kelvin wave forcing around 15 hPa among the reanalyses, as well as the different magnitudes, shown in Fig. 11 may imply a limitation in quantifying wave forcing of the QBO using a reanalysis dataset. Advances in observation and assimilation of stratospheric waves might be needed to reduce the spread of the assimilated waves and to further improve global models. In addition, given that the representation of equatorial waves in reanalyses is dependent on the assimilated mean winds (Fig. 11), the reality of small-scale gravity-wave parameterization in forecast models, which can affect the details of the QBO winds, might also be important for the assessment of the large-scale wave forcing. The rather weak magnitudes of the MRG wave forcing in the easterly-shear zone in all of the reanalyses imply that other waves (especially gravity waves) might play a more important role in driving the easterly phase of the QBO than MRG waves (Kawatani et al., 2010; Evan et al., 2012; Ern et al., 2014) and/or that current observational measurements, as well as models and assimilation methods, cannot fully capture the MRG waves which have relatively small vertical wavelengths. Modeling studies have demonstrated that adequate representation of the stratospheric equatorial waves requires vertical resolutions of ∼700 m or finer in the lower to middle stratosphere (Giorgetta et al., 2006; Richter et al., 2014), while the vertical spacings of the prediction models used for the current reanalyses are about a factor of 2 larger than that (Table 1). It is noteworthy that the aforementioned simulation of locally generated MRG waves by Garcia and Richter (2019) used a 500 m vertical resolution, in which the MRG waves induced large momentum forcing (∼10 m s−1 month−1), although they did not act to drive the QBO but to neutralize the westerly jet.
In the k–ω spectrum for the symmetric component of meridional wind (Fig. 2), a distinct spectral peak is seen at 20 hPa, which stretches toward high frequencies and high wavenumbers from around ω∼0.4 cyc d−1 and . To investigate this further, we filter a part of the spectrum that does not coincide with the spectrum of the lower-frequency MRG waves investigated in Sect. 3. The filtered spectral region is cyc d−1 for and cyc d−1 for . Figure 13 presents time series of variances of the filtered meridional-wind spectrum at 20 and 10 hPa, along with the observed near-Equator zonal wind at each altitude compiled by FUB. For all reanalyses, it is clearly seen that this spectral peak appears only when the background wind is easterly with substantial speeds at each altitude. Furthermore, there exist time lags of the variance peaks between the two altitudes, as well as a lag in the zonal wind due to the downward progression of the QBO. Due to these time lags, there exist periods during which the variance is large at 10 hPa, while it is much smaller at 20 hPa at the same time (e.g., late 1999/early 2000 and late 2008/early 2009). This indicates that the spectral signal of these waves does not originate from below. On the other hand, there also exist periods during which the variance is much larger at 20 hPa than at 10 hPa (e.g., late 2007), suggesting that the waves at 20 hPa are, at least in part, generated in situ. In fact, the vertical EP flux of this spectrum is not well identified (see Fig. 10), which could indicate a minimal preference for upward or downward propagation of the waves. This also could be suggestive of in situ wave generation. This spectral peak is also seen in the upper stratosphere above 10 hPa, although it is less evident here because the peak is not clearly separated from that of the lower-frequency waves (not shown).
Given the dependence of that spectrum filtered for and −8 upon the background wind U (Fig. 13), the entire spectrum of those waves can be more clearly identified by compositing for the periods with strong background easterlies. Figure 14 presents two composites of the symmetric meridional-wind spectrum for the months with m s−1 and m s−1 at 20 hPa, based on the FUB zonal wind. The composite result is shown only for JRA-55C (in which the amplitude of this spectrum is the largest in Fig. 2) but is qualitatively similar for the other reanalyses. For m s−1, it is shown that the spectrum has peaks at and −5 with periods of about 2 d. The ground-based zonal phase speeds corresponding to the peaks are between −45 and −60 m s−1. These are much higher compared to those of the waves detected in the westerly QBO wind in Maury and Lott (2014) and Garcia and Richter (2019) discussed in Sect. 3.4 (about −20 m s−1; see also Fig. 11, the first and last rows). The spectral region is best identified by the dispersion curves of MRG waves (Fig. 14) rather than the other types of waves, provided that m s−1. The spectrum composited for m s−1 is similar to that of the lower-frequency MRG waves observed in the lower stratosphere. The variances of the symmetric meridional wind by the waves observed at 20–10 hPa during the easterly QBO phase typically have magnitudes of roughly half of those by the lower-frequency MRG waves during the westerly phase (not shown).
The high-frequency waves detected here have similar characteristics to the quasi-two-day wave (QTDW) observed in the summer mesosphere and uppermost stratosphere: the QTDW also occurs in strong easterly winds with a ∼2 d period. It has been proposed that the QTDW is a MRG mode triggered by the baroclinic and/or barotropic instabilities associated with the easterly jet in the summer mesosphere (e.g., Salby, 1981; Pfister, 1985; McCormack et al., 2009). However, given that the occurrence of the 20 hPa disturbances is strongly tied to certain phases of the QBO, as seen in Figs. 13 and 14, they might not be necessarily connected from the QTDW above. More details on the structure of these waves and their possible impacts in the tropical stratosphere will be pursued in a future study.
The equatorial Kelvin and MRG waves in the TTL and stratosphere represented in six reanalyses (ERA-I, MERRA, MERRA-2, CFSR, JRA-55, and JRA-55C) are compared for the period of 1981–2010. The power spectra with respect to the zonal wavenumber and frequency are presented (Figs. 1 and 2). The spectral shapes of the Kelvin and MRG waves are broadly similar among the reanalyses: they exhibit common spectral peaks and widths as well as vertical variations of the spectral shapes, except for the Kelvin waves above 100 hPa in CFSR. The stratospheric Kelvin waves in CFSR have remarkably larger powers at relatively low-frequency, low-equivalent-depth ranges than in the others. JRA-55 and JRA-55C show relatively smaller temperature amplitudes than the other reanalyses, common to all altitudes below 20 hPa.
The spatial distributions and patterns of the equatorial waves in the lower stratosphere are investigated (Figs. 3–5). It is shown in all of the reanalyses that Kelvin and MRG wave variances tend to be large in the eastern and western hemispheres, respectively, and that the locations of their maxima tilt eastward in the vertical. However, the longitudinal variations of the Kelvin wave variances are much smaller in CFSR compared to those in the others. The leading mode EOFs of the Kelvin wave and MRG wave filtered perturbations are used to obtain statistically representative patterns of the waves in each reanalysis, following Kiladis et al. (2016). For both waves, the horizontal-wind and geopotential perturbations projected onto the leading EOFs show spatial patterns and phase relationships between variables that are consistent with the classical equatorial wave theory. All the reanalyses studied here exhibit remarkably similar patterns for the Kelvin wave leading modes, which have zonal wavenumber 1 structures with larger amplitudes in the eastern hemisphere. The MRG wave leading modes are confined over the eastern Pacific to Atlantic sector and also show reasonable agreement between the reanalyses, although their zonal scales are somewhat larger in CFSR.
From analysis of the time series of Kelvin and MRG wave variances, systematic differences are found between the periods before and after the late 1990s in several aspects (Figs. 6–8).
-
The difference in the Kelvin wave variances between JRA-55 and JRA-55C (which stems from the exclusion of satellite data in the assimilation in JRA-55C) shows significant changes after the late 1990s at 100 hPa (from ∼7 % to 10 %–24 %) and at 10 and 5 hPa (from between 0 and −10 % to 10 %–20 %) but not at ∼50 hPa (Fig. 7).
-
The Kelvin wave variances in the middle and upper stratosphere in ERA-I exhibit a large increase around 1998 (∼50 %), becoming significantly larger than those in the other reanalyses (Figs. 8 and S3).
-
In the middle and upper stratosphere in MERRA-2, the peaks of the Kelvin wave variances during westerly-shear phases of the QBO are not represented in some years before the mid-1990s (Fig. S3). The MRG wave variances at 10 hPa show exceptionally large values during the westerly-shear phases until 1998 but not afterward.
-
The MRG wave variances in CFSR fluctuate largely in the vertical from ∼30 hPa before 1998 but not afterward (Fig. 8).
The results listed here demonstrate significant impacts of the TOVS–ATOVS transition starting in 1998 on the assimilated wave amplitudes in the middle and upper stratosphere in all the reanalyses. Below 10 hPa, the satellite impacts on the waves are identifiable in JRA-55 only by direct comparison with JRA-55C at 100 hPa where the SSU instruments in the TOVS suite do not cover.
The time series of the Kelvin wave variances at 100 hPa (Fig. 6) exhibit increasing trends in all the reanalyses except JRA-55C. However, the veracity of the trends in Kelvin wave activity is uncertain due to potential satellite effects in the reanalyses. On the other hand, the MRG wave variances show a long-term increase at 100 hPa, common to all of the reanalyses including JRA-55C which is not affected by satellite transitions.
It is also noted that variances of equatorial waves can be underestimated by up to around 30 % when standard-pressure-level datasets are used. The wave perturbations in these datasets are damped out by vertical interpolation, and the damping effect is large for waves with small vertical wavelengths.
The EP flux and its divergence are presented as a function of phase speed and height to compare the QBO forcing measured in the reanalyses (Figs. 11 and 12). In general, the phase speeds at which the Kelvin wave forcing occurs are comparable among ERA-I, MERRA-2, JRA-55, and JRA-55C. The Kelvin wave EP flux is the largest in ERA-I, while its forcing is larger in MERRA-2 with more severe dissipation of the waves. For the QBO phases with westerly acceleration at ∼15 hPa, the height of the peak forcing differs between the reanalyses by up to ∼3 km. The differences in the dissipation rate and peak forcing altitude are found to be related to the different mean-wind profiles in the reanalyses. The MRG wave forcing is in general small in all the reanalyses (up to ∼3 m s−1 month−1 for the 5∘ N–5∘ S average).
In addition, relatively high-frequency waves detected in the spectra of symmetric meridional winds at 20 hPa (Fig. 2), which are distinguishable from the MRG waves observed below, are further investigated (Figs. 13 and 14). It is found in all the reanalyses that they appear only when the background wind is easterly, unlike the MRG waves propagating from below, with ground-based periods of about 1–3 d. Their spectral shape is best identified by the dispersion curve of MRG waves with the background wind of about −30 m s−1. More details regarding the spatial pattern, origin, and implication of these waves remain to be studied in the future.
The ERA-Interim data can be obtained from https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim and the MERRA and MERRA-2 data from https://disc.gsfc.nasa.gov/datasets. The CFSR data can be downloaded from https://www.ncei.noaa.gov/thredds/catalog/cfs_reanl_ts/catalog.html and the JRA-55 and JRA-55C data can be found in https://jra.kishou.go.jp/JRA-55/index_en.html. The near-Equator monthly zonal wind from the radiosonde observations compiled by FUB can be found in https://www.geo.fu-berlin.de/en/met/ag/strat/produkte/qbo/index.html.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-10027-2019-supplement.
The EOF analysis in Sect. 3.2 was carried out by GNK, JRA, and JD, and the other calculations were by YHK. The initial idea for the paper was provided by MF and JA. All authors provided further ideas and contributed to the interpretation of the results. The manuscript was written first by YHK with advice from CY, except Sect. 3.2, which was written by JRA and GNK. All authors contributed to improvement/correction of the manuscript.
The authors declare that they have no conflict of interest.
This article is part of the special issue “The SPARC Reanalysis Intercomparison Project (S-RIP) (ACP/ESSD inter-journal SI)”. It is not associated with a conference.
The authors thank Rolando R. Garcia and two anonymous referees for their constructive review comments.
This study was supported by the National Research Foundation of Korea (NRF-2016R1C1B2006310, NRF-2018R1A6A1A08025520). Masatomo Fujiwara was financially supported in part by the Japan Society for the Promotion of Science (JSPS) KAKENHI (JP26287117, JP16K05548, and JP18H01286), and Yoshio Kawatani was also supported by JPSP KAKENHI (JP15KK0178, JP17K18816, and JP18H01286). Corwin J. Wright was funded by a Royal Society University Research Fellowship (UF160545) and by Natural Environment Research Council (NE/R001391/1).
This paper was edited by Timothy J. Dunkerton and reviewed by Rolando R. Garcia and two anonymous referees.
Alexander, S. P., Tsuda, T., Kawatani, Y., and Takahashi, M.: Global distribution of atmospheric waves in the equatorial upper troposphere and lower stratosphere: COSMIC observations of wave mean flow interactions, J. Geophys. Res., 113, D24115, https://doi.org/10.1029/2008JD010039, 2008. a
Andrews, D. G., Holton, J. R., and Leovy, C. B.: Middle Atmosphere Dynamics, Academic, San Diego, California, 489 pp., 1987. a
Baldwin, M. P., Gray, L. J., Dunkerton, T. J., Hamilton, K., Haynes, P. H., Randel, W. J., Holton, J. R., Alexander, M. J., Hirota, I., Horinouchi, T., Jones, D. B. A., Kinnersley, J. S., Marquardt, C., Sato, K., and Takahashi, M.: The quasi-biennial oscillation, Rev. Geophys., 39, 179–229, https://doi.org/10.1029/1999RG000073, 2001. a
Birner, T., Sankey, D., and Shepherd, T. G.: The tropopause inversion layer in models and analyses, Geophys. Res. Lett., 33, L14804, https://doi.org/10.1029/2006GL026549, 2006. a
Bloom, S. C., Takacs, L. L., da Silva, A. M., and Ledvina, D.: Data Assimilation Using Incremental Analysis Updates, Mon. Weather Rev., 124, 1256–1271, https://doi.org/10.1175/1520-0493(1996)124<1256:DAUIAU>2.0.CO;2, 1996. a
Boehm, M. T. and Verlinde, J.: Stratospheric influence on upper tropospheric tropical cirrus, Geophys. Res. Lett., 27, 3209–3212, https://doi.org/10.1029/2000GL011678, 2000. a
Coy, L., Wargan, K., Molod, A. M., McCarty, W. R., and Pawson, S.: Structure and Dynamics of the Quasi-Biennial Oscillation in MERRA-2, J. Climate, 29, 5339–5354, https://doi.org/10.1175/JCLI-D-15-0809.1, 2016. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Dickinson, M. and Molinari, J.: Mixed Rossby–Gravity Waves and Western Pacific Tropical Cyclogenesis, Part I: Synoptic Evolution, J. Atmos. Sci., 59, 2183–2196, https://doi.org/10.1175/1520-0469(2002)059<2183:MRGWAW>2.0.CO;2, 2002. a
Dunkerton, T. J.: The role of gravity waves in the quasi-biennial oscillation, J. Geophys. Res., 102, 26053–26076, https://doi.org/10.1029/96JD02999, 1997. a
Ern, M., Preusse, P., Krebsbach, M., Mlynczak, M. G., and Russell III, J. M.: Equatorial wave analysis from SABER and ECMWF temperatures, Atmos. Chem. Phys., 8, 845–869, https://doi.org/10.5194/acp-8-845-2008, 2008. a
Ern, M., Ploeger, F., Preusse, P., Gille, J. C., Gray, L. J., Kalisch, S., Mlynczak, M. G., Russell III, J. M., and Riese, M.: Interaction of gravity waves with the QBO: A satellite perspective, J. Geophys. Res., 119, 2329–2355, https://doi.org/10.1002/2013JD020731, 2014. a
Evan, S., Alexander, M. J., and Dudhia, J.: WRF simulations of convectively generated gravity waves in opposite QBO phases, J. Geophys. Res., 117, D12117, https://doi.org/10.1029/2011JD017302, 2012. a
Flannaghan, T. J. and Fueglistaler, S.: The importance of the tropical tropopause layer for equatorial Kelvin wave propagation, J. Geophys. Res., 118, 5160–5175, https://doi.org/10.1002/jgrd.50418, 2013. a
Fueglistaler, S., Dessler, A. E., Dunkerton, T. J., Folkins, I., Fu, Q., and Mote, P. W.: Tropical tropopause layer, Rev. Geophys., 47, RG1004, https://doi.org/10.1029/2008RG000267, 2009. a
Fujiwara, M., Kita, K., and Ogawa, T.: Stratosphere-troposphere exchange of ozone associated with the equatorial Kelvin wave as observed with ozonesondes and rawinsondes, J. Geophys. Res., 103, 19173–19182, https://doi.org/10.1029/98JD01419, 1998. a
Fujiwara, M., Hasebe, F., Shiotani, M., Nishi, N., Vömel, H., and Oltmans, S. J.: Water vapor control at the tropopause by equatorial Kelvin waves observed over the Galápagos, Geophys. Res. Lett., 28, 3143–3146, https://doi.org/10.1029/2001GL013310, 2001. a
Fujiwara, M., Suzuki, J., Gettelman, A., Hegglin, M. I., Akiyoshi, H., and Shibata, K.: Wave activity in the tropical tropopause layer in seven reanalysis and four chemistry climate model data sets, J. Geophys. Res., 117, D12105, https://doi.org/10.1029/2011JD016808, 2012. a, b, c, d
Fujiwara, M., Wright, J. S., Manney, G. L., Gray, L. J., Anstey, J., Birner, T., Davis, S., Gerber, E. P., Harvey, V. L., Hegglin, M. I., Homeyer, C. R., Knox, J. A., Krüger, K., Lambert, A., Long, C. S., Martineau, P., Molod, A., Monge-Sanz, B. M., Santee, M. L., Tegtmeier, S., Chabrillat, S., Tan, D. G. H., Jackson, D. R., Polavarapu, S., Compo, G. P., Dragani, R., Ebisuzaki, W., Harada, Y., Kobayashi, C., McCarty, W., Onogi, K., Pawson, S., Simmons, A., Wargan, K., Whitaker, J. S., and Zou, C.-Z.: Introduction to the SPARC Reanalysis Intercomparison Project (S-RIP) and overview of the reanalysis systems, Atmos. Chem. Phys., 17, 1417–1452, https://doi.org/10.5194/acp-17-1417-2017, 2017. a, b, c, d
Garcia, R. R. and Richter, J. H.: On the Momentum Budget of the Quasi-Biennial Oscillation in the Whole Atmosphere Community Climate Model, J. Atmos. Sci., 76, 69–87, https://doi.org/10.1175/JAS-D-18-0088.1, 2019. a, b, c, d
Garcia, R. R. and Salby, M. L.: Transient response to localized episodic heating in the tropics, Part II: Far-field behavior, J. Atmos. Sci., 44, 499–530, https://doi.org/10.1175/1520-0469(1987)044<0499:TRTLEH>2.0.CO;2, 1987. a
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G.-K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017. a
Giorgetta, M. A., Manzini, E., Roeckner, E., Esch, M., and Bengtsson, L.: Climatology and forcing of the quasi-biennial oscillation in the MAECHAM5 model, J. Climate, 19, 3882–3901, https://doi.org/10.1175/JCLI3830.1, 2006. a
Grise, K. M., Thompson, D. W. J., and Birner, T.: A Global Survey of Static Stability in the Stratosphere and Upper Troposphere, J. Climate, 23, 2275–2292, https://doi.org/10.1175/2009JCLI3369.1, 2010. a
Hendon, H. H. and Wheeler, M. C.: Some Space–Time Spectral Analyses of Tropical Convection and Planetary-Scale Waves, J. Atmos. Sci., 65, 2936–2948, https://doi.org/10.1175/2008JAS2675.1, 2008. a, b
Holton, J. R. and Lindzen, R. S.: An updated theory for the quasi-biennial cycle of the tropical stratosphere, J. Atmos. Sci., 29, 1076–1080, https://doi.org/10.1175/1520-0469(1972)029<1076:AUTFTQ>2.0.CO;2, 1972. a
Immler, F., Krüger, K., Fujiwara, M., Verver, G., Rex, M., and Schrems, O.: Correlation between equatorial Kelvin waves and the occurrence of extremely thin ice clouds at the tropical tropopause, Atmos. Chem. Phys., 8, 4019–4026, https://doi.org/10.5194/acp-8-4019-2008, 2008. a
Kawatani, Y., Watanabe, S., Sato, K., Dunkerton, T. J., Miyahara, S., and Takahashi, M.: The Roles of Equatorial Trapped Waves and Internal Inertia–Gravity Waves in Driving the Quasi-Biennial Oscillation, Part I: Zonal Mean Wave Forcing, J. Atmos. Sci., 67, 963–980, https://doi.org/10.1175/2009JAS3222.1, 2010. a
Kawatani, Y., Hamilton, K., Miyazaki, K., Fujiwara, M., and Anstey, J. A.: Representation of the tropical stratospheric zonal wind in global atmospheric reanalyses, Atmos. Chem. Phys., 16, 6681–6699, https://doi.org/10.5194/acp-16-6681-2016, 2016. a, b, c, d, e
Kiladis, G. N., Dias, J., and Gehne, M.: The Relationship between Equatorial Mixed Rossby–Gravity and Eastward Inertio-Gravity Waves, Part I, J. Atmos. Sci., 73, 2123–2145, https://doi.org/10.1175/JAS-D-15-0230.1, 2016. a, b, c, d
Kim, J. and Son, S.-W.: Tropical Cold-Point Tropopause: Climatology, Seasonal Cycle, and Intraseasonal Variability Derived from COSMIC GPS Radio Occultation Measurements, J. Climate, 25, 5343–5360, https://doi.org/10.1175/JCLI-D-11-00554.1, 2012. a
Kim, J.-E. and Alexander, M. J.: A new wave scheme for trajectory simulations of stratospheric water vapor, Geophys. Res. Lett., 40, 5286–5290, https://doi.org/10.1002/grl.50963, 2013. a
Kim, J.-E. and Alexander, M. J.: Direct impacts of waves on tropical cold point tropopause temperature, Geophys. Res. Lett., 42, 1584–1592, https://doi.org/10.1002/2014GL062737, 2015. a
Kim, Y.-H. and Chun, H.-Y.: Momentum forcing of the quasi-biennial oscillation by equatorial waves in recent reanalyses, Atmos. Chem. Phys., 15, 6577–6587, https://doi.org/10.5194/acp-15-6577-2015, 2015a. a, b, c
Kim, Y.-H. and Chun, H.-Y.: Contributions of equatorial wave modes and parameterized gravity waves to the tropical QBO in HadGEM2, J. Geophys. Res., 120, 1065–1090, https://doi.org/10.1002/2014JD022174, 2015b. a, b
Kobayashi, C., Endo, H., Ota, Y., Kobayashi, S., Onoda, H., Harada, Y., Onogi, K., and Kamahori, H.: Preliminary results of the JRA-55C, an atmospheric reanalysis assimilating conventional observations only, SOLA, 10, 78–82, https://doi.org/10.2151/sola.2014-016, 2014. a
Kobayashi, S., Ota, Y., Harada, Y., Ebita, A., Moriya, M., Onoda, H., Onogi, K., Kamahori, H., Kobayashi, C., Endo, H., Miyaoka, K., and Takahashi, K.: The JRA-55 reanalysis: General specifications and basic characteristics, J. Meteorol. Soc. Jpn., 93, 5–48, https://doi.org/10.2151/jmsj.2015-001, 2015. a
Lott, F., Kuttippurath, J., and Vial, F.: A climatology of the gravest waves in the equatorial lower and middle stratosphere: Method and results for the ERA-40 re-analysis and the LMDz GCM, J. Atmos. Sci., 66, 1327–1346, https://doi.org/10.1175/2008JAS2880.1, 2009. a
Lott, F., Denvil, S., Butchart, N., Cagnazzo, C., Giorgetta, M. A., Hardiman, S. C., Manzini, E., Krismer, T., Duvel, J.-P., Maury, P., Scinocca, J. F., Watanabe, S., and Yukimoto, S.: Kelvin and Rossby-gravity wave packets in the lower stratosphere of some high-top CMIP5 models, J. Geophys. Res., 119, 2156–2173, https://doi.org/10.1002/2013JD020797, 2014. a
Matsuno, T.: Quasi-geostrophic motions in the equatorial area, J. Meteorol. Soc. Jpn., 44, 25–43, https://doi.org/10.2151/jmsj1965.44.1_25, 1966. a
Maury, P. and Lott, F.: On the presence of equatorial waves in the lower stratosphere of a general circulation model, Atmos. Chem. Phys., 14, 1869–1880, https://doi.org/10.5194/acp-14-1869-2014, 2014. a, b
McCormack, J. P., Coy, L., and Hoppel, K. W.: Evolution of the quasi 2-day wave during January 2006, J. Geophys. Res., 114, D20115, https://doi.org/10.1029/2009JD012239, 2009. a
Onogi, K., Tsutsui, J., Koide, H., Sakamoto, M., Kobayashi, S., Hatsushika, H., Matsumoto, T., Yamazaki, N., Kamahori, H., Takahashi, K., Kadokura, S., Wada, K., Kato, K., Oyama, R., Ose, T., Mannoji, N., and Taira, R.: The JRA-25 Reanalysis, J. Meteorol. Soc. Jpn., 85, 369–432, https://doi.org/10.2151/jmsj.85.369, 2007. a
Pfister, L.: Baroclinic instability of easterly jets with applications to the summer mesosphere, J. Atmos. Sci., 42, 313–330, https://doi.org/10.1175/1520-0469(1985)042<0313:BIOEJW>2.0.CO;2, 1985. a
Plumb, R. A.: Stratospheric transport, J. Meteorol. Soc. Jpn., 80, 793–809, https://doi.org/10.2151/jmsj.80.793, 2002. a
Plumb, R. A. and Bell, R. C.: Equatorial waves in steady zonal shear flow, Q. J. R. Meteorol. Soc., 108, 313–334, https://doi.org/10.1002/qj.49710845603, 1982. a
Randel, W. J. and Wu, F.: Kelvin wave variability near the equatorial tropopause observed in GPS radio occultation measurements, J. Geophys. Res., 110, D03102, https://doi.org/10.1029/2004JD005006, 2005. a, b
Randel, W. J., Boville, B. A., and Gille, J. C.: Observations of planetary mixed Rossby-gravity waves in the upper stratosphere., J. Atmos. Sci., 47, 3092–3099, https://doi.org/10.1175/1520-0469(1990)047<3092:OOPMRW>2.0.CO;2, 1990. a
Richter, J. H., Solomon, A., and Bacmeister, J. T.: On the simulation of the quasi-biennial oscillation in the Community Atmosphere Model, Version 5, J. Geophys. Res., 119, 3045–3062, https://doi.org/10.1002/2013JD021122, 2014. a
Rienecker, M. M., Suarez, M. J., Gelaro, R., Todling, R., Backmeister, J., Liu, E., Bosilovich, M. G., Schubert, S. D., Takacs, L., Kim, G.-K., Bloom, S., Chen, J., Collins, D., Conaty, A., da Silva, A., Gu, W., Joiner, J., Koster, R. D., Lucchesi, R., Molod, A., Owens, T., Pawson, S., Pegion, P., Redder, C. R., Reichle, R., Robertson, F. R., Ruddick, A. G., Sienkiewicz, M., and Woollen, J.: MERRA: NASA's Modern-Era Retrospective Analysis for Research and Applications, J. Climate, 24, 3624–3648, https://doi.org/10.1175/JCLI-D-11-00015.1, 2011. a
Ryu, J.-H., Alexander, M. J., and Ortland, D. A.: Equatorial Waves in the Upper Troposphere and Lower Stratosphere Forced by Latent Heating Estimated from TRMM Rain Rates, J. Atmos. Sci., 68, 2321–2342, https://doi.org/10.1175/2011JAS3647.1, 2011. a
Saha, S., Moorthi, S., Pan, H.-L., Wu, X., Wang, J., Nadiga, S., Tripp, P., Kistler, R., Woollen, J., Behringer, D., Liu, H., Stokes, D., Grumbine, R., Gayno, G., Hou, Y.-T., Chuang, H., Juang, H.-M. H., Sela, J., Iredell, M., Treadon, R., Kleist, D., Delst, P. V., Keyser, D., Derber, J., Ek, M., Meng, J., Wei, H., Yang, R., Lord, S., van den Dool, H., Kumar, A., Wang, W., Long, C., Chelliah, M., Xue, Y., Huang, B., Schemm, J.-K., Ebisuzaki, W., Lin, R., Xie, P., Chen, M., Zhou, S., Higgins, W., Zou, C.-Z., Liu, Q., Chen, Y., Han, Y., Cucurull, L., Reynolds, R. W., Rutledge, G., and Goldberg, M.: The NCEP climate forecast system reanalysis, B. Am. Meteorol. Soc., 91, 1015–1057, https://doi.org/10.1175/2010BAMS3001.1, 2010. a
Salby, M. L.: Rossby normal modes in nonuniform background configurations. Part II: Equinox and solstice conditions, J. Atmos. Sci., 38, 1827–1840, https://doi.org/10.1175/1520-0469(1981)038<1827:RNMINB>2.0.CO;2, 1981. a
Salby, M. L. and Garcia, R. R.: Transient response to localized episodic heating in the tropics. Part I: Excitation and short-time near-field behavior, J. Atmos. Sci., 44, 458–498, https://doi.org/10.1175/1520-0469(1987)044<0458:TRTLEH>2.0.CO;2, 1987. a
Scherllin-Pirscher, B., Randel, W. J., and Kim, J.: Tropical temperature variability and Kelvin-wave activity in the UTLS from GPS RO measurements, Atmos. Chem. Phys., 17, 793–806, https://doi.org/10.5194/acp-17-793-2017, 2017. a
Simmons, A. J., Poli, P., Dee, D. P., Berrisford, P., Hersbach, H., Kobayashi, S., and Peubey, C.: Estimating low-frequency variability and trends in atmospheric temperature using ERA-Interim, Q. J. Roy. Meteor. Soc., 140, 329–353, https://doi.org/10.1002/qj.2317, 2014. a
Smith, W. L., Woolf, H. M., Hayden, C. M., Wark, D. Q., and McMillin, L. M.: The TIROS-N Operational Vertical Sounder, B. Am. Meteorol. Soc., 58, 1177–1187, https://doi.org/10.1175/1520-0477-60.10.1177, 1979. a
Tsuda, T., Murayama, Y., Wiryosumarto, H., Harijono, S. W. B., and Kato, S.: Radiosonde observations of equatorial atmosphere dynamics over Indonesia: 1. Equatorial waves and diurnal tides, J. Geophys. Res., 99, 10491–10505, https://doi.org/10.1029/94JD00355, 1994. a
Wheeler, M. and Kiladis, G. N.: Convectively coupled equatorial waves: Analysis of clouds and temperature in the wavenumber–frequency domain, J. Atmos. Sci., 56, 374–399, https://doi.org/10.1175/1520-0469(1999)056<0374:CCEWAO>2.0.CO;2, 1999. a, b
Wright, J. S., Fujiwara, M., Long, C., Anstey, J., Chabrillat, S., Compo, G. P., Dragani, R., Ebisuzaki, W., Harada, Y., Kobayashi, C., McCarty, W., Molod, A., Onogi, K., Pawson, S., Simmons, A., Tan, D. G. H., Tegtmeier, S., Wargan, K., Whitaker, J. S., and Zou, C.-Z.: Description of the Reanalysis Systems, in: SPARC Reanalysis Intercomparison Project (S-RIP), Chap. 2, in review, 2019. a
Yang, G.-Y., Hoskins, B., and Gray, L.: The influence of the QBO on the propagation of equatorial waves into the stratosphere, J. Atmos. Sci., 69, 2959–2982, https://doi.org/10.1175/JAS-D-11-0342.1, 2012. a, b, c, d
Zhou, X. and Wang, B.: Transition from an eastern Pacific upper-level mixed Rossby-gravity wave to a western Pacific tropical cyclone, Geophys. Res. Lett., 34, L24801, https://doi.org/10.1029/2007GL031831, 2007. a
Prior to this procedure, we converted the k–ω spectra to much finer resolution in frequency using linear interpolation for each k. This is required because the frequency resolution of the original spectra ( cyc d−1) is coarse in terms of c for small k (e.g., for k=1, m s), causing artificial peaks and noise. For the finer spectra, we set Δω to be 500 times smaller than the original, after confirming that the results converge without displaying artificial peaks for varying Δω around such values.