Valley floor inclination affecting valley winds and transport of passive tracers in idealised simulations

In mountainous regions, diurnal thermally driven winds impact daily weather and air quality. This study investigates how the inclination of idealised valleys affects these winds and the transport of passive tracers using high-resolution numerical simulations with the Weather Research and Forecasting (WRF) model. We explore a range of valley inclinations from 0 to 2.28°, bridging the gap between previous studies on flat and moderately inclined (up to 0.86°) idealised valleys and steeper (2–5°) real Himalayan valleys. We find that during daytime in the inclined valleys, up-valley winds penetrate deeper into the valleys and become stronger, up to a critical inclination beyond which the winds weaken. The flat-floored valley exhibits the strongest night-time down-valley winds overall, but surface-based down-valley winds are more prominent in inclined valleys. Steeper valleys enhance the vertical transport of passive tracers, resulting in ventilation at higher altitudes compared to the flat-floored valley. Despite stronger overall tracer outflow in the flat-floored valley, this occurs at lower altitudes, leading to most of the ventilated tracers being accumulated in the lowest few kilometres of the atmosphere. Consequently, steeper valleys are more efficient at ventilating tracers to the upper troposphere, which would, for example, lead to higher potential for long-range transport. These findings underscore the critical role of valley geometry in shaping wind patterns and pollutant transport, providing valuable insights for improving transport modelling in mountainous regions.

1 Introduction

In mountainous areas, daily weather and air quality are influenced by thermally driven winds that flow up the valleys and slopes during the day and down during the night (Whiteman, 2000). Diurnal valley and slope winds form due to horizontal temperature gradients that develop due to topography-induced differential heating of the lowest part of the atmosphere. Although pollutants emitted near the surface can be trapped in the valley atmosphere for days (Whiteman et al., 2014), the daytime winds are efficient in transporting the mass (i.e. air pollution) to the free troposphere – also referred to as mountain venting (Serafin et al., 2018). Once in the free troposphere, aerosol can affect the climate, for example, by altering cloud formation (Gordon et al., 2017) and can be transported long distances (Henne et al., 2004), affecting regions far away from the actual emission location. Modelling these transport processes in the mountain valleys is demanding, especially on global scales (Rotach et al., 2014), as resolving them accurately requires at least kilometre-scale grid spacing in model simulations (Wagner et al., 2014).

Daytime up-slope winds are a result of buoyancy forcing, as the air near the heated slope surface is warmer than the air away from the slope at the same altitude (Vergeiner and Dreiseitl, 1987; Farina and Zardi, 2023). Above the up-slope wind layer a flow forms towards the valley centre with descending motion at the valley centre. Depending on the valley shape, the cross-valley circulation often consists of two or more vertically stacked cells separated by stable inversion layers (Wagner et al., 2015b). Similarly to the daytime counterpart, night-time down-slope winds form as the air near the cooling surface cools down and becomes denser than air away from the slope (Vergeiner and Dreiseitl, 1987). The cross-valley slope winds respond quickly to the thermal forcing from the heated or cooled sloped surface and thus develop and reach their maxima soon after sunrise and sunset (Vergeiner and Dreiseitl, 1987). Up-slope and down-slope winds are often referred to as anabatic and katabatic winds, respectively. In this article the term “anabatic winds” refers to winds flowing up and “katabatic winds” to winds flowing down an inclined surface. This applies regardless of whether these are valley winds along an inclined valley floor or slope winds that flow in a cross-valley direction. Important factors for the development of the anabatic and katabatic winds regarding this study are the background stability and slope angle (Vergeiner and Dreiseitl, 1987, Eq. 5). Increased background stability and a steeper slope angle would decrease the along-slope mass flux (e.g. Schmidli, 2013, Eq. 9) as a result of a shallower flow depth (Farina and Zardi, 2023, Eq. 10).

Daytime plain-to-valley and up-valley winds in the along-valley direction form due to the temperature gradient which develops between the valley atmosphere and the air above the adjacent plain (Whiteman, 2000). The temperature gradient is traditionally explained by the concept of the topographic amplification factor (TAF; Zardi and Whiteman, 2013), also referred to as the valley volume effect. Due to its confined geometry, a valley exhibits a smaller air volume beneath a horizontal reference surface, e.g. located at crest height, than the volume over the foreland. This smaller air volume is associated with a smaller air mass and, when subjected to the same amount of energy input, experiences a larger heating rate than the larger air mass over the foreland. However, TAF is considered to be the theoretical maximum for the heat deficit, as some of the heat is exported out of the valley volume by the cross-valley circulation (Schmidli, 2013). Using the same volume comparison but with surface cooling, the night-time down-valley winds and valley-to-plain winds form due to a reversed pressure gradient (Whiteman, 2000). The along-valley winds develop much slower than the cross-valley up-slope winds, as the driving pressure gradient force is based on the warming or cooling of the valley atmosphere instead of the shallow layer near the slope surface.

The daytime cross-valley circulation is efficient in transporting mass (i.e. air pollution) up to the ridge height from the valley bottom and slopes (Serafin et al., 2018), where often most of the emission sources are located. Along-valley winds contribute to horizontal transport through the larger-scale air exchange between the valley atmosphere and the surrounding plains as well as within the different parts along the valley (Gohm et al., 2009). Bianchi et al. (2021) suggested the daytime up-valley winds play an important role for ventilation of biogenic aerosol out of a Himalayan valley at high altitudes. Using in situ aerosol measurements in the Khumbu valley combined with Lagrangian transport modelling, they found that the daytime up-valley winds transported aerosol up to 5 km altitude within the valley volume, which was followed by ventilation into the free troposphere at the head of the valley. Transport of pollutants to the high altitudes within the Khumbu valley (Hindman and Upadhyay, 2002; Bonasoni et al., 2010) and into the free troposphere by the local valley circulation (Venzac et al., 2008) has been identified by other studies in the past. Bianchi et al. (2021) suggested that the southern slope of the Himalayas could act as a large source of free-tropospheric aerosol, as other valleys in the mountain range could also have similar ventilation processes. Mikkola et al. (2023) compared the daytime up-valley winds in the Khumbu valley to three other major valleys nearby. Based on their comparison of the up-valley wind characteristics, the other three valleys would also have the potential for ventilation. Differences in the modelled up-valley winds across these valleys were hypothesised to stem from differences in terrain geometry, particularly valley floor steepness.

The valley winds and their associated transport processes are sensitive e.g. to the valley geometry (i.e. width, depth, narrowing, inclination, or curvature; Wagner et al., 2015a; Weigel et al., 2006), synoptic-scale winds and pressure gradients (Whiteman and Doran, 1993), temperature stratification (vertical profile of temperature; Schmidli and Rotunno, 2015), and valley surface properties (i.e. albedo and surface roughness; Gohm et al., 2009). Effects of the valley geometry on the valley winds and transport processes in mountain regions have been studied in the past by numerous measurement campaigns and numerical modelling studies, using both real (e.g. Zängl et al., 2001; Weigel et al., 2006) and idealised (e.g. Li and Atkinson, 1999; Schmidli and Rotunno, 2015; Wagner et al., 2015b; Leukauf et al., 2017; Göbel et al., 2023) topographies. Although Wagner wrote as early as 1938 about slope winds that form above and flow along inclined valley floors (Whiteman and Dreiseitl, 1984), studies which investigate the effect of valley floor inclination on the up-valley winds are (to the authors' best knowledge) almost absent from the literature. Exceptions are Wagner et al. (2015a) and Mikkola et al. (2023).

Wagner et al. (2015a) studied the effect of along-valley topographic heterogeneity on the daytime up-valley winds and transport processes by means of idealised WRF simulations (Weather Research and Forecasting model). Valley floor inclination was one of the topographic factors they varied systematically. Their valleys had constant ridge heights of 1.5 km and in their steepest case the valley floor was inclined at 0.86°. With a constant ridge height, the inclination of the valley floor leads to reduced valley volume and would strengthen the valley volume effect. For example, in the steepest case of Wagner et al. (2015a), the valley volume is reduced by half compared to a flat-floored valley. Wagner et al. (2015a) found the valley floor inclination to strengthen the up-valley winds through a combination of enhanced valley volume effect and additional buoyancy forcing along the inclined valley floor. For example, they found that the steepest valley floor inclination (0.86°) enhanced the daytime up-valley winds by a factor of 3.0. However, they did not quantify the relative contribution of these two effects. Mikkola et al. (2023) compared four Himalayan valleys in high-resolution WRF simulations. Parts of these valleys were inclined between 2 and 5°. They found that the steepest parts of the valleys were associated with both weak and shallow daytime up-valley winds. Mikkola et al. (2023) suggested that the contradiction in their results compared to Wagner et al. (2015a) is caused by the notable difference in the topographies of the studied valleys. The Himalayan valleys studied by Mikkola et al. (2023) are much steeper than the idealised valleys in Wagner et al. (2015a), so the up-slope buoyancy forcing was suggested to have a larger role than the valley volume effect in driving the up-valley winds. Also, the valley volume effect is not necessarily enhanced in the Himalayan valleys due to the valley floor inclination, as the valley ridges are inclined as well. When the height difference between the valley centre and ridge lines stays constant along the valley, the volume of air does not change even though the valley topography would be tilted at an angle.

In this article, we study how the valley inclination affects the valley winds and transport of passive tracers out of idealised mountain valleys. We perform numerical meteorological simulations using WRF (Skamarock et al., 2019) with idealised topographies. Our simulations fill the gap between Wagner et al. (2015a) and Mikkola et al. (2023) by extending the range of valley inclinations to also include steeper valleys than what was used in Wagner et al. (2015a) and by tilting the valley ridges similar to the Himalayan valleys studied in Mikkola et al. (2023). In addition, we study how the location of the tracer release affects the tracer ventilation. We study how changing the along and cross-valley location of the tracer release affects the transport of the tracer mass and at what altitude the tracers end up from valleys with different inclinations.

First, the methodology including the model setup and data analysis methods is introduced in Sect. 2. The valley flows are described in Sect. 3.1 and the transport of the passive tracers is described in Sect. 3.2. The results are discussed and compared to previous studies in Sect. 4, and conclusions are given in Sect. 5.

2 Methods

2.1 Model setup

In this study, we use the Weather Research and Forecasting model (WRF) version 4.4.1 (Skamarock et al., 2019). For flux computation and online averaging we use a budget calculation tool, WRFlux (Göbel et al., 2022), which is a fork of the original WRF available online (GitHub repository, Göbel, 2022). Data analysis methods are described in detail in Sect. 2.4. The WRF model domain has a size of 200 km in the y direction (along-valley) and 40 km in the x direction (cross-valley) and a horizontal grid spacing of 200 m. The model domain has 140 model levels, with the lowest model level at 15 m above the surface and the model top at 20 km height. The vertical model level spacing is less than or equal to 100 m below the height of 5 km and has a maximum value of 308.25 m (Fig. S1 in the Supplement). A w-Rayleigh damping layer with a depth of 8 km is applied at the model top. Lateral boundaries are symmetric in the y direction and periodic in the x direction.

WRF is run in LES (large-eddy simulation) mode, which uses three-dimensional 1.5-order TKE (turbulent kinetic energy) closure for turbulence, a third-order Runge–Kutta time integration scheme, fifth-order horizontal advection, and third-order vertical advection of momentum and scalars. Microphysics are parameterised using the WRF single-moment scheme (Hong and Lim, 2006; WSM6 scheme). Surface layer physics are parameterised using the revised MM5 similarity theory (Jiménez et al., 2012).

The simulations are initialised at 06:00 local time (LT) in the morning and run for 48 h with a time step of 2 s. Surface sensible heat flux, H, is prescribed to follow a diurnal cycle defined by

$$\begin{array}{}\text{(1)}& H\left(t\right)=max\left(H_{\text{max}}\sin \left({\displaystyle \frac{\mathrm{2}\mathit{\pi }}{\mathrm{24}\text{h}}}t\right),H_{\text{min}}\right),\end{array}$$

where t is time in hours since the simulation start, H_max=150 W m⁻², and $H_{\text{min}}=-\mathrm{10}$ W m⁻² (time series of H shown in Fig. S2). Values of H_max and H_min are based on the real-case WRF simulations covering the Nepal Himalayas used in Mikkola et al. (2023). Wagner et al. (2015a) and Schmidli and Rotunno (2010) both used similar prescribed diurnal cycles of the sensible heat flux in their idealised valley simulations. Moisture flux and latent heat flux at the surface are described by the surface layer model, although the surface sensible heat flux is prescribed. The domain is initialised with relative humidity of zero on all model levels. The model domain has homogeneous surface properties defined as evergreen needle-leaf forest (USGS 24-category land use table), following the dominant land use type in the Himalayan valleys studied in Mikkola et al. (2023).

The initial temperature profile of the simulation is based on a 40-year climatology of Decembers in 1979–2019 in the eastern Nepal Himalayas (26–28° N, 86–88° E) in ERA5 reanalysis (Hersbach et al., 2020). December is generally a favourable period for studying thermally driven valley winds in the region due the frequent clear skies and strong diurnal temperature cycle (Bollasina et al., 2002; Bonasoni et al., 2010). The initial vertical profile of the ideal WRF simulations and the ERA5 long-term average profiles are shown in Fig. S3. In our simulations, the initial state is defined using a base temperature of 295 K at 1000 hPa, a constant Brunt–Väisälä frequency of 0.11 s⁻¹, and horizontal wind components set to zero.

2.2 Idealised topographies

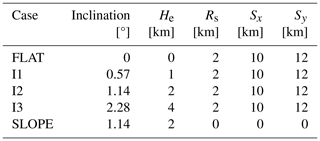
The idealised topographies used in this study are shown in Fig. 1. The topographies are defined following Wagner et al. (2015a) and Schmidli and Rotunno (2010), with an addition for the along-valley inclination. The simulated cases consists of four different valley topographies and one slope experiment. The simulated valleys are 100 km long in the y direction and have a cosine shape in the x direction with 20 km width (ridge to ridge) and 2 km depth (valley centre to ridge height difference). The valleys differ from each other by the angle of the linear increase in the surface height in the y direction. The slope experiment has the same domain size and a linear increase in the surface in the y direction without the shape of a valley. The remaining half of the model domain in the y direction is covered by a flat plain in all simulations. Using a notation where the valley centre line across the centre of the valley is located along x=0 km and the ridge height of 2 km is reached at y=0 km, the valley topographies are defined by

$$\begin{array}{}\text{(2)}& \begin{array}{rl}h(x,y)& =\left(R_{\mathrm{s}}{h}_{\mathrm{r}}\left(y\right)-h_{\mathrm{c}}\left(y\right)\right)\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\cos \left(\mathit{\pi }{\displaystyle \frac{\left|x\right|}{S_x}}\right)\right)\\ & +h_{\mathrm{c}}\left(y\right),\end{array}\end{array}$$

where R_s is the valley depth, h_r(y) is the along-valley height profile of the ridge, h_c(y) is the along-valley profile of the valley centre (x=0), and S_x is half-width of the valley (also the length of the slope in the x direction). The along-valley height profile of the valley centre, h_c(y), is defined by

$$\begin{array}{}\text{(3)}& h_{\mathrm{c}}\left(y\right)=\left\{\begin{array}{ll}\mathrm{0},& y\le \mathrm{0}\\ \frac{H_{\mathrm{e}}}{L_y}y,& y>\mathrm{0},\end{array}\right.\end{array}$$

where L_y is the length of the valley and H_e is the valley centre height at the end of the valley (y=L_y). The along-valley profile of the ridges is defined by

$$\begin{array}{}\text{(4)}& h_{\mathrm{r}}\left(y\right)=\left\{\begin{array}{ll}\mathrm{0},& y\le -S_y\\ \frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\cos \left(\frac{\mathit{\pi }}{S_y}y\right)& -S_y<y<\mathrm{0}\\ \mathrm{1}+\frac{H_{\mathrm{e}}}{R_s{L}_y}y& y>\mathrm{0}\end{array},\right.\end{array}$$

where S_y is the length in the y direction over which the ridges increase in height to their full depth of 2 km at the valley entrance.

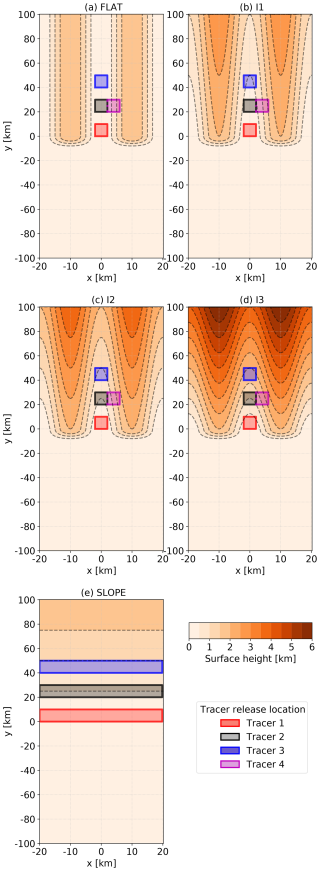
Figure 1 Model topography in cases (a) FLAT, (b) I1, (c) I2, (d) I3, and (e) SLOPE. Dashed lines show the topography on 500 m contours. Tracer release locations are shown by colour-filled boxes.

The topography parameters for the simulated cases used in Eqs. (2)–(4) are given in Table 1. The only difference between the four simulated valleys is the along-valley inclination of the valley floor and ridges. One of the valleys has a flat valley centre height and a constant ridge height of 2 km (referred to as case FLAT; Fig. 1a). The other three valleys are inclined so that the height of the valley floors increases linearly to 1 km (referred to as case I1; Fig. 1b), 2 km (case I2; Fig. 1c), and 4 km (case I3; Fig. 1d). In all of the valleys, the valley centre to ridge height difference remains 2 km, meaning that the valley shape in the cross-valley direction remains the same for all of the valleys in all of their parts. The slope experiment (referred to as case SLOPE; Fig. 1e) is a 100 km long slope inclined to reach 2 km height. The valley topographies are motivated by the Himalayan valleys studied by Mikkola et al. (2023). The steepest case in our experiments, I3, is representative by the inclination, width, and depth of the Khumbu valley, which leads to the base of Mt. Everest.

Table 1 Topography parameters for Eqs. (2)–(4) in the simulated cases. An explanation for H_e, R_s, S_x, and S_y is found in the main text. Values in the column “Inclination” are the tilt of the valley floors and ridges in the along-valley direction for y=0 to 100 km, i.e. $\arctan (H_{\mathrm{e}}/\mathrm{100}\mathrm{km})$.

2.3 Passive tracers

Transport processes are studied using passive tracers. In order to study the importance of the emission location, four passive tracers are released at different along-valley and cross-valley locations. Implementation of the passive tracers is done following the model setup by Lang et al. (2015). Tracer release locations are shown by colour in Fig. 1 and in Tables S1 and S2 in the Supplement. Three along-valley locations ($\mathrm{0}\mathrm{km}<y<\mathrm{10}\mathrm{km}$, $\mathrm{20}\mathrm{km}<y<\mathrm{30}\mathrm{km}$, and $\mathrm{40}\mathrm{km}<y<\mathrm{50}\mathrm{km}$) are selected around the valley centre line ($-\mathrm{2}\mathrm{km}<x<\mathrm{2}\mathrm{km}$) and one location on the right-hand side slope ($\mathrm{20}\mathrm{km}<y<\mathrm{30}\mathrm{km}$, $\mathrm{2}\mathrm{km}<x<\mathrm{6}\mathrm{km}$). In case SLOPE there are three tracers released in the same along-valley locations as in the valley simulations, spanning the whole model domain in the x direction (Fig. 1e). The passive tracers are released at the six lowest model levels, which corresponds to an approximately 100 m deep surface-based layer. Technically the release happens through the addition of 1.0 g kg⁻¹ to the tracer mixing ratio in the selected grid boxes every model time step during 09:00–10:00 LT on the first morning of the simulation. Since the same numbers of grid boxes and model levels are used in the release for all of the valley topographies, the total tracer mass differs between the cases and tracers. As the release location is elevated along the inclined valleys but the released tracer mixing ratio is constant, the total tracer mass varies due to changes in the air density. Therefore, relative tracer mass and concentrations normalised by the total tracer mass in each simulation domain are shown in the analysis.

2.4 Data analysis

The analysis volumes are shown by the dotted lines in Fig. 2 for topography I3. In the analysis, the valley volume is referred to as the whole length of the valley (y=0 to 100 km) from ridge to ridge in the cross-valley direction ($x=-\mathrm{10}$ to 10 km) and below the ridge height in the vertical direction. The lower half of the valley is the volume between y=0 and 50 km and the top half of the valley is between y=50 and 100 km. The analysis equations can be found in Appendix A. The wind and tracer analysis considers mainly the valley at the centre ($\left|x\right|<\mathrm{10}$ km), in which the passive tracers are released. An identically shaped valley is located at $\left|x\right|>\mathrm{10}$ km (Fig. 1a–d), as the periodic boundary condition in the x direction joins the two valley halves between the main valley and the domain boundaries. This parallel valley is not included in the analysis if not clearly mentioned in the text. For the SLOPE case, the reference analysis volume is a 2 km deep layer above the sloped surface, which corresponds to the ridge height of the valley topographies, and the whole domain in the x direction.

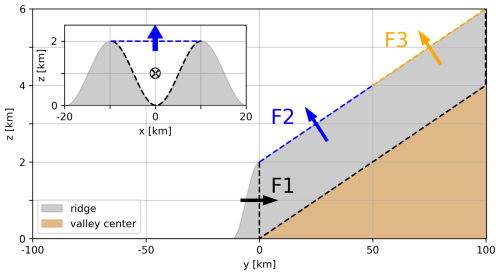
Figure 2 Flux components F1–F3 referred to in the analysis (case I3 topography shown). In the cross-valley direction F1 covers the whole valley ridge-to-ridge cross-section area and F2–F3 cover the whole width of the valley at ridge height (shown in the inset).

Tracer fluxes at the ridge height and at the valley entrance are computed using WRFlux v.1.4.1 (GitHub repository, Göbel, 2022), which is a budget calculation tool for WRF. Using WRFlux one can output the time-averaged fluxes decomposed into resolved and sub-grid-scale components transformed into Cartesian coordinates (Göbel et al., 2022). Other tendency terms are also available but we use only the mean flow and sub-grid-scale flux components in the analysis. Flux computations for the passive tracer fields were added to WRFlux v1.4.1 following the computation of the moisture flux (water vapour mixing ratio flux). Hourly averaged tracer fluxes in the x–y–z directions for mean flow and sub-grid-scale components are used in the analysis.

Arrows F1–F3 in Fig. 2 show the flux components considered for the passive tracers. F1 is the horizontal transport into and out of the volume at the valley entrance. F2 and F3 are the flux of tracers through the upper lid of the valley volume at the ridge height in the lower half and upper half of the valley, respectively. F2 and F3 are normal to the valley inclination, meaning they consider not only the vertical tracer flux but also the y direction of the tracer flux through the upper lid of the valley volume at the ridge height. For case SLOPE, the flux components are the same as those shown by F1–F3, but they account for the entire domain in the x direction due to the homogeneity of the slope.

3 Results

3.1 Valley winds

In this section, the wind fields of the five simulations are described and compared. First, in Sect. 3.1.1–3.1.3 the spatial structures of the valley winds are analysed, which is followed by a description of the temporal evolution in Sect. 3.1.4. The valley circulation comparison is summarised with time and volume integrals in Sect. 3.1.5. For clarity, case SLOPE is always compared to valley simulation I2 (which has the same inclination) separately from the comparison between the valley simulations.

3.1.1 Spatial structure of the wind and potential temperature during day 1

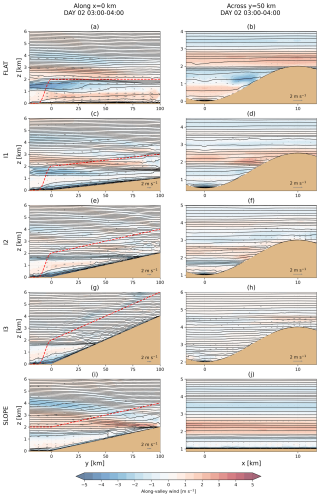
Figures 3 and 4 show the vertical cross-sections along the valley centres (along x=0 km, left column) and across the half-way point of the valleys (across y=50 km, right column). Figure 3 shows the average for 15:00–16:00 LT on the first day and Fig. 4 for 03:00–04:00 LT on the first night. The same figures but for the second day and night are shown in Figs. S4 and S5, respectively.

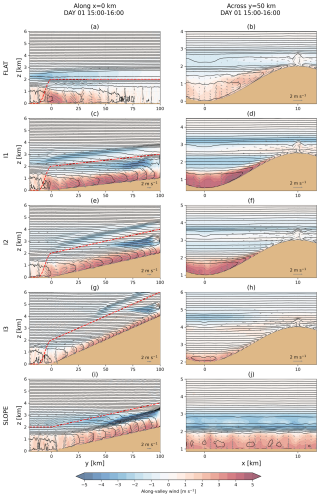
Figure 3 Vertical cross-sections along the domain centres at x = 0 km (a, c, e, g, i) and across the domain at y = 50 km (b, d, f, h, j). For all panels the along-valley wind is shaded (positive for up-valley wind, 0.5 m s⁻¹ interval) and potential temperature is plotted on contours (0.5 K interval). Grey vectors show the wind component in the plotted plane. The plotted values are an hourly average of 15:00–16:00 LT on the first day of the simulation.

Figure 4 Same as Fig. 3 but for 03:00–04:00 LT on the first night of the simulation.

Daytime up-valley winds and plain-to-valley winds form in all the simulations (Fig. 3). On the first day the convective boundary layer (CBL) over the plain, in which the plain-to-valley winds flow, grows up to 1.5 km above the surface (y < 0 km in Fig. 3a, c, e, and g). The potential temperature contours (isentropes) in the valley cases FLAT, I1, I2, and I3 exhibit a structure that is typical for up-valley winds (Fig. 3a, c, e, and g). The CBL in the valley warms up more than the CBL above the plain, which is seen as the isentropes turning towards the surface from the inversion top of the CBL in the valley. The along-valley circulation consists of single or multiple cells, varying between the valleys. Down-valley-directed return flow of the main circulation cell is located right above the inversion top of the surface-based up-valley wind layer. A typical near-surface structure for isentropes associated with anabatic up-slope winds is seen in the cross-valley direction (Fig. 3b, d, f, and h) but also in the along-valley direction in the inclined valleys (Fig. 3c, e, and g). The near-surface layer of air warms more than the air at the same altitude but located away from the slope, which is seen as a sharp turn of the isentropes downwards near the surface.

Two abbreviations for the convective boundary layer in the simulations are introduced for clarity and used hereafter. CBL_v refers to the surface-based unstable/neutral layer in the valley in which the up-valley winds flow and hence the layer with the strongest up-valley winds (dark red in Fig. 3). The depth and absolute height of the CBL_v change along the valleys and evolve through the course of the diurnal cycle. CBL_p refers to the surface-based unstable/neutral layer above the plain in which the plain-to-valley winds flow. CBL_p has about constant depth throughout the plain but changes in time. For example, on the first day between 15:00 and 16:00 LT the CBL_p depth is about 1.5 km (Fig. 3). CBL_v and CBL_p are used in this study to qualitatively describe the valley's temperature distribution, not as quantitative measurements.

A few major differences in the daytime valley circulation between the simulations were identified in the along-valley cross-sections (Fig. 3a, c, e, and g).

• The up-valley winds penetrate further up into the inclined valleys when compared to case FLAT.

• Within the inclined valleys the up-valley winds become weaker and shallower with increasing inclination.

• Inclined valleys have multiple circulation cells in the along-valley direction, whereas case FLAT only has one circulation cell.

These differences are described in detail in the following paragraphs.

The daytime up-valley winds reach further up into the inclined valleys (Fig. 3c, e, and g) compared to case FLAT (Fig. 3a). In case FLAT the strongest up-valley winds are found near the valley entrance, which is followed by weaker winds further in the valley. Near the valley entrance the maximum up-valley wind speeds reach up to 3.5 m s⁻¹ and decrease down to less than 1.5 m s⁻¹ within the first 25 km at the valley centre x=0 km (at 15:00–16:00 LT on the first day of the simulation; Fig. 3a). At the head of the valley (y>75 km), the along-valley winds are less than 0.5 m s⁻¹. In the inclined valleys the up-valley winds reach the head of the valley with almost constant strength along the valley (Fig. 3c, e, and g) but with decreasing up-valley wind speed with increasing inclination. The up-valley wind speeds reach up to 4 m s⁻¹ in case I1 (Fig. 3c), 3.5 m s⁻¹ in case I2 (Fig. 3e), and 3 m s⁻¹ in case I3 (Fig. 3g). In the inclined valleys, near the surface, a similar structure of the isentropes in the along-valley direction to what would typically be associated with anabatic up-slope winds is found. This suggests that the buoyancy-driven anabatic winds are contributing in the daytime to the up-valley winds near the surface. This is caused by the inclined heated valley surface, which likely causes a horizontal temperature gradient in the along-valley direction not only in the valley entrance region as in FLAT but also continuously along the whole inclined valley as is also typical for up-slope winds.

Near the valley entrance the flow depth of the up-valley winds is same for all the valleys (Fig. 3a, c, e, and g) and roughly corresponds to the depth of the CBL_p (1.5 km in Fig. 3a, c, e, and g). Further up in the valleys, the flow depth decreases with increasing valley inclination. The depth of the up-valley wind layer is limited from above by the capping inversion of the CBL_v. The CBL_v depth varies by location within the valleys. Above the CBL_v, away from the heated valley surface, the atmosphere is stably stratified. In case FLAT the CBL_v depth slightly decreases along the valley (Fig. 3a), whereas in all other valleys it strongly decreases (Fig. 3c, e, and g). This implies that in most inclined valleys a large portion of the valley atmosphere is stably stratified. This fraction increases with increasing inclination. In the inclined valleys the height of the CBL_v decreases to a constant depth, which also decreases with increasing inclination of the valley. Near the head of the valley where the up-valley winds encounter the domain boundary, the CBL_v depth changes (discussed later in this section).

The along-valley circulation in the valleys consists of a singular circulation cell in case FLAT (Fig. 3a) and multiple cells in the inclined valleys (Fig. 3c, e, and g). The along-valley and vertical location of the down-valley-directed return flow of the main circulation cell varies between the valleys. Here the term main circulation cell refers to the surface-based up-valley wind layer in CBL_v and the strongest return flow directly above it. In case FLAT, the return flow is located mostly above the valley volume around the altitude of 1.5 to 3 km, and it is strongest above the valley entrance ($\left|y\right|<\mathrm{10}$ km; Fig. 3a). In the inclined valleys, the return flow is located mostly inside the valley volume with varying altitudes due to the elevation along the valleys (Fig. 3c, e, and g). The strongest wind speeds in the return flow are found near the head of the valley (y>75 km) and vertically in the upper 1 km of the valley volume. The altitude of the return flow in the inclined cases is between 2 and 3 km for case I1 (Fig. 3c), between 2.5 and 3.5 km for case I2 (Fig. 3e), and between 4 and 5 km for case I3 (Fig. 3g). The strong return flow near the head of the valley in the inclined valleys is likely caused by the symmetric boundary conditions that lead to forced convergence near y=100 km. Likely driven by the buoyancy force generated by the heating of inclined valley floors, up-valley winds extend all the way to the y boundary at the head of the valley.

A secondary circulation cell in the along-valley direction forms in the inclined valleys, clearly present only in cases I1 (Fig. 3c and d) and I2 (Fig. 3e and f). The secondary circulation cell is shallower and weaker than the main circulation cell and is located above the ridge height. That this circulation forms only above the inclined valleys and not in case FLAT is likely related to the elevated near-neutral and/or less stable layer which is found around the ridge height (Fig. 3b, d, f, and h). The near-neutral layer around the ridge height is the most pronounced in case FLAT (Fig. 3b), with decreasing presence with increasing inclination (Fig. 3d, f, and h). These elevated layers likely form due to subsidence warming in the valley core and the diverging horizontal flow from the ridge tops ($x=\pm \mathrm{10}$ km) towards the valley centre (Schmidli, 2013). The elevated warmed layer gets weaker with increasing valley inclination, likely due to weakening cross-valley circulation. The elevated near-neutral layer is located around the ridge height for each along-valley point (i.e. along the y coordinate) of the valley. For the inclined cases the altitude of this layer increases along the valleys (Fig. 3c, e, and g). Now, along the whole length of the valley, the elevated near-neutral layer is warmer than the air at the same altitude towards the plain. This temperature gradient is likely to form the secondary circulation cell in the along-valley direction. This secondary cell does not form in case FLAT since the elevated near-neutral layer is at the same altitude for each along-valley point of the valley (z≈2.5 km; Fig. 3a).

Similarly to the inclined valley cases, in case SLOPE the daytime plain-to-slope winds are limited between the sloped surface and the inversion top of the local CBL (Fig. 3i). The plain-to-slope winds are weaker than in case I2, especially at the beginning of the slope (y=0 km), which corresponds to the valley entrance of I2. The along-valley circulation consists of one prominent cell in case SLOPE. The down-valley return flow in case SLOPE is much stronger and shallower and is located below the 2 km reference height. In the x direction, there is nothing in particular happening in case SLOPE as the slope is homogeneous in this direction and the variation in the flow field is very small.

3.1.2 Spatial structure of the wind and potential temperature during day 2

On the second day of the simulation (Fig. S4), the patterns of plain-to-valley and up-valley winds are very similar to those simulated on the first day. Up-valley wind speeds are not notably different between the first (Fig. 3) and second day (Fig. S4) at 15:00–16:00 LT in the afternoon. The main difference between the 2 d is the deeper plain-to-valley and up-valley winds on the second day, which also implies deeper CBL_p and CBL_v. The larger magnitude of the prescribed surface sensible heat flux during daytime than during night-time results in a net heating of the boundary layer during the course of a full daily cycle, which explains the deeper CBL on the second day (2 km, Fig. S4a, c, e, and g) than on the first day (1.5 km, Fig. 3a, c, e, and g).

Since the surface-based up-valley winds flow in a deeper layer on the second day, the return flows are also located higher up. In case FLAT the return flow is located completely above the valley volume (Fig. S4a and b). In the inclined cases I1–I3 the return flow is also located higher but still below the ridge height in the valley volume (Fig. S4c, e, and g). The spatial extent of the return flow is similar to that on the first day, but the secondary circulation cells are much more prominent on the second day with stronger wind speeds.

3.1.3 Spatial structure of the wind and potential temperature during night-time

The night-time along-valley winds in the simulations consist of three major components, which are surface-based down-valley winds and up-valley winds in the residual layer with associated down-valley return flow (Fig. 4). In addition, a secondary circulation with weak up- and down-valley-directed winds forms above the valley volumes.

Surface-based down-valley winds form in all of the valleys (Fig. 4). In case FLAT this down-valley wind layer is less than a few tens of metres deep and the wind speed is negligibly weak (vertical profiles shown in Fig. S7). At the valley exit (y=0 km) in the inclined valleys, the surface-based down-valley winds have a maximum wind speed around 4 m s⁻¹ at the height of 100 m and the wind turns up-valley at around the height of 600 m. The surface-based down-valley winds in the inclined valleys are likely intensified by the katabatic wind mechanism acting along the cooled valley slopes. Strong inversions form in valleys I2 and I3 at the same altitude as the top of the residual layer at the plain and above this altitude the atmosphere is stably stratified (Fig. 4e–h). The inversion also forms in cases FLAT and I1 but has similar strength only near the head of the valleys. In the stably stratified part of valleys I2 and I3 the surface-based katabatic down-valley winds flow in a shallow layer of less than 100 m (Fig. S7). This could be explained by the katabatic wind strength and depth being inversely proportional to the background stability (e.g. Vergeiner and Dreiseitl, 1987, Eq. 5), and hence the katabatic down-valley winds in the near-neutral residual layer are stronger and flow in a deeper layer.

During night-time there are up-valley winds in the core of the valley volumes above the aforementioned surface-based down-valley winds (Fig. 4). A down-valley return flow is found below the inversion capping the residual layer, which maintains a relatively constant altitude from the plains into the valleys. This circulation spatially dominates the night-time along-valley winds in case FLAT and has a decreasing role with increasing inclination. The residual layer in the valley volume remains warmer than the air above the plain at the same height, which is likely the reason for these up-valley winds. After the surface heating turns into cooling at 18:00 LT, the strongest up-valley winds from the entrance in case FLAT start spreading further up into the valley, eventually reaching the head of the valley (Fig. 4a). In case I1 (Fig. 4c) these winds extend up to the head of the valley (y=100), but in the steeper valleys I2 (Fig. 4e) and I3 (Fig. 4g) the along-valley extent is limited to the distance where the valley floor reaches the height of the top of the residual layer. In the inclined valleys the surface-based down-valley winds occupy a deeper layer, which leaves less space in the valley atmosphere for the residual layer (Fig. 4c, e, and g).

Case SLOPE has night-time up-slope-directed winds in the residual layer (Fig. 4i). In case SLOPE these up-slope winds and the down-slope return flow are weaker than in case I2 (Fig. 4e). Katabatic down-slope winds also form in case SLOPE (Fig. 4i) but they are weaker and shallower compared to case I2 (Fig. 4e). The additional down-slope winds towards the valley centre in the cross-valley direction likely enhance the strength and depth of the katabatic down-valley winds at the valley centre (x=0 km) in case I2. The strong step in the isentropes in case SLOPE around y=50 km resembles a hydraulic jump which forms in the boundary of the residual layer and its inversion top. Similar flow structures in katabatic winds are identified, for example, in Yu et al. (2005).

The second night of the simulation (Fig. S5) has similar flow structures as the first night. The inversion top is located higher up, which gives more volume and along-valley distance for the up-valley winds in the residual layer and their associated return flow to develop. The increased inversion height also means that the katabatic down-valley winds in the inclined valleys obtain a deeper flow depth at the valley entrance due to the longer along-valley distance between the inversion and the valley entrance. In addition, the secondary circulation cell located above the inversion is stronger during the second night.

3.1.4 Temporal evolution of the spatially averaged along-valley winds

Time series of the valley-volume-averaged along-valley wind speed for each case are shown in Fig. 5a. The averaging volume for case SLOPE is a 2 km deep layer above the sloped surface. A diurnal cycle of up-valley winds during the day and down-valley winds during the night develops in all of the simulations. The daily maxima of the along-valley winds are fairly similar between the valley simulations on the first day, ranging between 0.5 and 0.75 m s⁻¹. On the second day the daytime along-valley wind maxima clearly weaken with valley inclination, as the daytime maximum in case FLAT is around 3 times the maximum of case I3. Similarly, the night-time down-valley winds weaken with steeper valley inclination. Both the daytime up-valley winds and night-time down-valley winds reach their maximum earlier with increasing inclination of the valley.

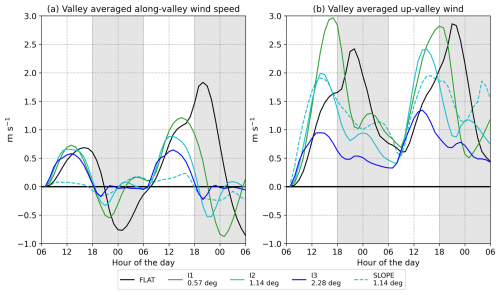
Figure 5 Time series of the valley-volume-averaged (a) along-valley wind speed and (b) up-valley wind speed. Shown values are hourly averages plotted at the start of the averaged hour. Positive values refer to up-valley wind. For the valleys (cases FLAT, I1, I2, I3) the averaging volume is shown as dashed lines in Fig. 2. For case SLOPE the averaging volume is a 2 km deep layer above the sloped surface. Time steps with negative surface sensible heat flux are indicated by grey shading.

When considering the valley-volume-averaged along-valley wind it would appear that case FLAT clearly has the strongest up-valley winds. This difference is due to the down-valley-directed return flow, which is mostly outside the valley volume in case FLAT (Sect. 3.1.1) and, therefore, does not affect the valley volume average as much as in the inclined cases. Since we are particularly interested in the daytime up-valley winds and their potentially crucial role in the transport of tracers from the valley atmosphere to the free troposphere, we also show the averaged up-valley wind component in Fig. 5b. In this latter case, only positive values of the along-valley wind component are averaged, which avoids compensation due to negative values associated with the return flow. For a detailed explanation of how the shown variable in Fig. 5b is computed, refer to Appendix A1.1. On the first day, the maximum magnitudes of the valley-averaged up-valley winds vary between 1 and 3 m s⁻¹ (Fig. 5b). The strongest up-valley winds occur in case I1 and the weakest in case I3, which aligns with Fig. 3 discussed in Sect. 3.1.1. On the second day, case FLAT has just slightly higher maximum up-valley winds, but the difference to I1 is less than 0.1 m s⁻¹ (Fig. 5b).

In steeper valleys, the daytime up-valley wind speed (Fig. 5b) more closely follows the temporal evolution of the surface sensible heat flux (Fig. S2). The time of maximum up-valley wind speed varies across cases, ranging from 13:00 LT for case I3 to 21:00 LT for case FLAT. This indicates that steeper valleys (like case I3) experience the most intense up-valley winds earlier in the day. Similarly, with increasing inclination the night-time down-valley winds form and peak earlier. This time difference could be explained by the response timescale of the anabatic up-valley winds compared to the valley-volume-effect-driven up-valley winds (Vergeiner and Dreiseitl, 1987). The plain-to-valley winds are driven by the pressure gradient which forms between the CBL_v and CBL_p. Anabatic winds flow in a shallower layer and require less time to build up to the same magnitude in wind speed. This is the reason for the anabatic up-valley winds forming shortly after the beginning of the surface heating, seen as stronger up-valley winds in the inclined valleys during the morning hours (Fig. 5b). The response timescale of the anabatic (and katabatic) winds is inversely proportional to the Brunt–Väisälä frequency and sine of the slope inclination (Schumann, 1990). The steeper the inclination of the valley, the larger the share of its volume of air that is stably stratified due to the shallower CBL_v, and hence the Brunt–Väisälä frequency is larger. Both of these factors increase with valley inclination, which explains the shorter response time during the morning and evening transition period for the steeper valleys.

On the second day, the valley-volume-averaged along-valley wind speeds are stronger compared to the first day (Fig. 5a). However, the valley-volume-averaged up-valley wind speeds do not increase with the same proportion (Fig. 5b). On the second day, the up-valley winds flow in a deeper layer as the CBL_v grows deeper (Sect. 3.1.1–3.1.2). Due to the deeper up-valley winds, the return flow is mostly or partly located above the valley volume and thus has less of a contribution to the valley-volume-averaged along-valley wind speeds (Fig. 5a). Case I1 is the only simulation which does not show an increase in the up-valley wind speeds on the second day (Fig. 5b).

The night-time down-valley winds peak earlier in the night with steeper valley inclination (Fig. 5a). Furthermore, the strength of the night-time down-valley winds decreases with increasing inclination. The down-valley return flows associated with the remaining night-time up-valley winds in the residual layer occupy a smaller volume of the valley atmosphere for the steeper valleys (discussed in Sect. 3.1.3), which explains the weaker valley-averaged down-valley winds. The earlier peak with steeper valley inclination would be explained by the response timescale discussed above.

In the volume-averaged along-slope wind, case SLOPE shows much weaker winds compared to case I2 (Fig. 5a). This is because its return flow is entirely located within the analysis volume (Sect. 3.1.1), which drastically reduces the volume-averaged up-slope wind. The 2 km deep analysis volume in case SLOPE was chosen to correspond to the ridge height in the valley simulations. However, when averaging only the positive along-slope winds, the flow strength in case SLOPE is comparable to that in case I2 (Fig. 5b). In the morning, the winds in case SLOPE are slightly stronger than those in the valley simulations.

3.1.5 Along-valley air mass transport

Figure 6 summarises how the average along-valley air mass transport varies with valley inclination and the time period over which it is integrated. The shown variable is the averaged horizontal along-valley mass flux, integrated over four different time periods: (1) the whole 48 h of the simulation (black circles), (2) when the valley-volume-averaged along-valley winds are positive (red squares), (3) times with non-negative surface sensible heat flux from 06:00 to 18:00 LT (blue triangles), and (4) times with negative surface sensible heat flux from 18:00 to 06:00 LT (purple crosses). Hereafter this variable is referred to as the air mass transport in the valley. For a detailed explanation of how the shown variable in Fig. 6 is derived, refer to Appendix A1.2.

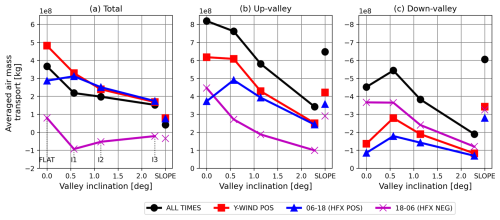
Figure 6 Time integral of the valley-averaged (a) total y-component mass flux, (b) positive y-component mass flux, and (c) negative y-component mass flux plotted against the valley inclination. Note that the y axis is inverted in panel (c) and the strength of the down-valley-directed transport increases with decreasing values. For case SLOPE the averaging volume is a 2 km deep layer above the sloped surface. Four time periods are considered: (1) the whole 48 h simulation plotted as black dots, (2) the time steps with positive valley-volume-averaged along-valley wind plotted as red squares (time steps when Fig. 5a is positive), (3) time steps with non-negative surface sensible heat flux (06:00–18:00 LT) plotted as blue triangles, and (4) time steps with negative surface sensible heat flux (18:00–06:00 LT) plotted as purple crosses. Case SLOPE is plotted separately on the right-hand side of each panel. Due to the lack of sidewalls in case SLOPE, the values of SLOPE have been divided by 4 to have values corresponding to the valley simulations (see Fig. 2, area within the dashed lines compared to the whole width below 2 km height).

In general, the total air mass transport, which includes both the up- and down-valley transport (i.e. the net horizontal transport), decreases with increasing valley inclination during daytime (Fig. 6a). Similar behaviour is also seen when only the positive (i.e. up-valley) mass transport is considered (Fig. 6b). However, this result is sensitive to the time period over which the air mass transport is integrated, particularly in case FLAT. In this simulation, both the total air mass transport (Fig. 6a) and the positive air mass transport (Fig. 6b) are much lower when integrated over periods with positive surface sensible heat flux (blue triangles) compared to periods with positive averaged along-valley winds (red squares). This is because in case FLAT the along-valley winds remain positive longer than the surface sensible heat flux is positive (Fig. 5a), which is presumably due to the longer response timescale of the valley-volume-effect-driven up-valley winds than for the anabatic up-valley winds in the inclined cases. In contrast, for the inclined valleys, the along-valley wind component becomes negative around the time when the surface sensible heat flux turns negative. Therefore, for inclined valleys, the analysis period of positive along-valley winds (red squares) and the period of positive surface sensible heat flux of 06:00–18:00 LT (blue triangles) in Fig. 6a and b are similar.

The previous analysis suggests that a small inclination in the valley floor can enhance the daytime air mass transport, whereas a strong inclination reduces the air mass transport (06:00–18:00 LT, blue triangles in Fig. 6b). Within our simulations, case I1 with the inclination of 0.57° has the strongest daytime up-valley mass transport. We hypothesise that this is due to the contribution of the buoyancy force to the along valley winds. According to the theoretical model of Vergeiner and Dreiseitl (1987) for slope winds (their Eq. 5), the total mass flux of anabatic winds decreases with increasing surface slope and background stability. This would explain why the additional buoyancy forcing only increases the mass flux for shallow inclinations but not for steep ones. Moreover, the background stability, which determines the buoyancy forcing, is not the same in all simulations and also varies with height. Therefore, for small valley inclination (e.g. I1), the background stability is essentially determined by the CBL_p (Fig. 3c), implying weak stability. For strong valley inclination (e.g. I3), the stability is determined by the stably stratified atmosphere above the CBL_p (Fig. 3g), implying high stability. For intermediate inclinations (e.g. I2), there is a gradual transition from weak to strong background stratification as the valley winds pass the altitude of the CBL_p top. Consequently, a continuous decrease in the valley wind depth occurs along the valley (Fig. 3e), which aligns with the Prandtl model's prediction of an inverse relationship between the depth of the slope wind layer and the background stability (e.g. Farina and Zardi, 2023, Eq. 10). In summary, the strongest valley winds may occur at an optimal valley inclination. This inclination maximises the combined forcing of two factors: the valley volume effect, which arises from horizontal pressure gradients, and the slope flow effect, driven by buoyancy gradients.

The magnitude of the negative (i.e. down-valley) air mass transport during daytime decreases with increasing valley inclination for the inclined valleys (Fig. 6c). This means that the return flow during the day is weaker for steeper valleys; from a mass conservation point of view this is consistent with the positive mass flux, which also decreases with increasing inclination. Although the flat-floored valley appears to have a weaker return flow than the I1 case, this is only because the return flow in the flat case is above the 2 km deep averaging volume (Fig. 3a).

At night-time both the positive air mass transport and the magnitude of the negative air mass transport decrease with increasing valley inclination (purple crosses in Fig. 6b and c). It is noteworthy that for the flat-floored valley, the total mass transport remains positive (i.e. up valley) at night. This is caused by the strongest up-valley winds occurring in the evening, which are much stronger during the second day compared to the night-time down-valley winds (Sect. 3.1.4).

3.2 Tracer transport

In this section the transport of tracers in the simulations is described. First, the temporal evolution of tracer mass within the valley atmospheres is described in Sect. 3.2.1. The location and timing of the tracer mass flux out of the valleys are described in Sect. 3.2.2, and the final tracer mass distribution in the model domain is described in Sect. 3.2.3. The tracer analysis in this section considers only the main valley located at the centre of the domain ($\left|x\right|<\mathrm{10}$ km; Fig. 1) except in Sect. 3.2.3 where the parallel valley located at $\left|x\right|>\mathrm{10}$ km is taken into account as well. For a detailed description of how the shown variables in Figs. 7–10 are computed, refer to Appendix A2.

3.2.1 Time evolution of tracer mass in the valleys

Figure 7 shows the time series of relative tracer mass in the valley volumes (detailed description in Appendix A2). The relative tracer mass is the ratio of the tracer mass in the valley volume to the total tracer mass in the domain. For case SLOPE the reference volume is the 2 km layer above the sloped surface. The tracers are released in the first morning between 09:00 and 10:00 LT, which is shown by the red shading.

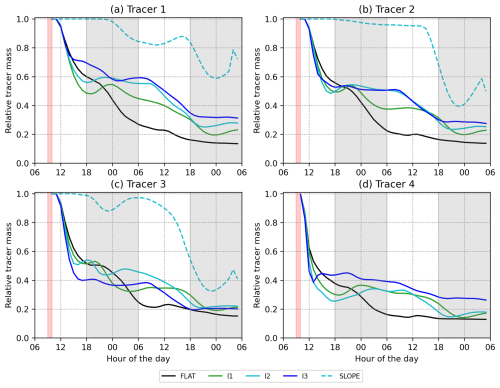
Figure 7 Time series of relative tracer mass within the valley volumes. A value of 1.0 corresponds to all the released tracer mass being within the valley atmosphere. For case SLOPE the reference volume is a 2 km layer above the sloped surface. See Fig. 1 for the tracer release locations. Red shaded areas denote the tracer release time and grey shaded areas the time steps with negative surface sensible heat flux.

The most intense transport of tracer mass out of the valleys happens during the first 6 h after the tracer release (Fig. 7). During these 6 h 30 %–70 % of the tracer mass is transported out of the valleys. Some of the tracer mass is re-injected back into the valley volumes, mostly during night-time, which is seen as an increase in the relative tracer mass with time. The strongest contrast in the valley tracer mass between case FLAT and the inclined valleys forms during the first night. During the first night the relative tracer mass decreases by 20 %–35 % in case FLAT. In the inclined valleys the relative tracer mass mostly stays approximately constant or changes less in magnitude compared to case FLAT. Around 09:00 LT on the second day the valley tracer mass starts decreasing again in the inclined valleys, coinciding with the formation of the up-valley and up-slope winds. During the last 6 h of the valley simulations the exchange of tracer mass between the valleys and their surroundings is very small.

The most notable difference among the four tracers is between tracer 4 (Fig. 7d) and the other tracers, 1–3 (Fig. 7a–c). Tracers 1–3 are released at the valley centre ($\left|x\right|<\mathrm{2}\mathrm{km}$), whereas tracer 4 is released at the slope ($\mathrm{2}\mathrm{km}<x<\mathrm{6}\mathrm{km}$). For tracer 4, the transport out of the valley atmosphere during the first 6 h is much more intensive since the tracer is released closer to the ridge height and also released directly into the cross-valley up-slope wind layer. However, the end result of the relative tracer mass in the valleys is almost the same for all of the tracers in each case.

The time evolution of the tracer mass within the reference volume differs a lot between case SLOPE (dashed line in Fig. 7) and valley simulation I2. During the first 24 h after the tracer release, at most 20 % of the tracer mass is transported out of the reference volume in case SLOPE. Only during the second afternoon of simulation SLOPE is a drastic drop of more than 40 % in tracers 2 and 3 seen. Strong re-injection of tracer mass back to the reference volume occurs for all of the tracers on the second night towards the end of the simulation.

3.2.2 Tracer flux out of the valleys

Figure 8 shows the time series of the flux components F1–F3 (see Sect. 2.4 and Appendix A2.2) for tracer 2 in the simulations. The same figures but for tracers 1, 3, and 4 are shown in Figs. S8–S10. Tracer 2 is shown here as it is released at the valley centre, not directly at the valley entrance, and its ventilation out of the valley is distributed the most evenly between the valley halves (discussed later in this section). Positive values refer to the flux direction shown in Fig. 2; hence, positive F1 refers to the horizontal transport of tracer mass from the plain into the valley at the valley entrance and positive F2–F3 refer to the ventilation of tracer mass out of the valley volume normal to the upper lid at the ridge height. The plotted variable (relative tracer flux in the unit of h⁻¹, for example, with a value of 0.1) means that 10 % of the tracer mass of that tracer in the whole domain is transported through the corresponding area during that hour.

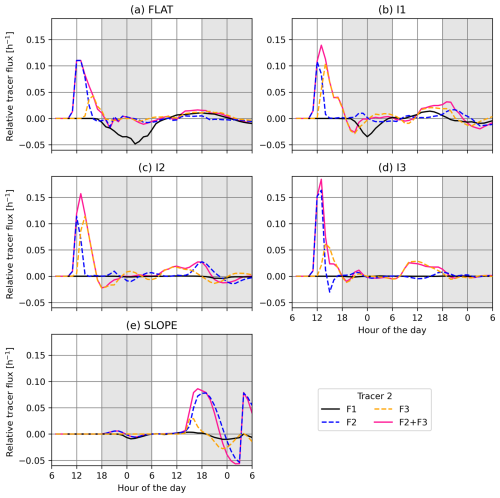
Figure 8 Time series of the flux components F1–F3 for tracer 2. The same figures but for tracers 1, 3, and 4 are shown in Figs. S8–S10. Tracer mass fluxes are normalised by the total tracer mass in the domain (of that tracer in that simulation case). Grey shaded areas show the time steps with negative surface sensible heat flux.

The aforementioned most intense flux of tracer mass between the valleys and their surroundings during the first 6 h after the tracer release occurs at the ridge height (Fig. 8a–d). For cases FLAT and I3 the vertical flux F2 (i.e. y<50 km) is clearly higher than F3 (i.e. y>50 km) on the first day (Fig. 8a and d). For cases I1 and I2 the ventilation is distributed more evenly between the two valley halves (Fig. 8b and c). These differences likely stem from the differences in the along-valley extent and strength of the daytime up-valley winds between the cases. In case FLAT the daytime up-valley winds do not extend far into the upper half (y>50 km) of the valley, so the ventilation by the cross-valley winds is more concentrated on F2. In case I3, although the up-valley winds do reach up to the head of the valley, the wind strength is lower, which results in weaker along-valley transport of tracer mass compared to cases I1 and I2.

For tracers 1 (Fig. S8) and 4 (Fig. S10) F2 is much higher than F3. Tracer 1 is released close to the valley entrance so the tracer mass has more time to ventilate in the lower half of the valley before reaching the top half of the valley. The ventilation of tracer 4 during the first 6 h following the release is double in magnitude compared to the other tracers since tracer 4 is released directly in the cross-valley up-slope circulation, so the tracer reaches the upper lid of the valley volume shortly after. Ventilation in the upper half of the valley (F3) is dominant for tracer 3 (Fig. S9) since this tracer is released at the half-way point of the valley and most of the tracer is transported rapidly into the upper half by the up-valley winds.

Horizontal transport of tracers between the valley volume and the plain occurs at the valley entrance, which is especially prominent during the night in cases FLAT and I1 (negative F1 in Fig. 8a and b). The transport to the plain coincides with the down-valley winds, which are also the strongest in cases FLAT and I1. The night-time residual layer up-valley winds and associated return flow most are likely the most important for the lateral tracer transport as the surface-based down-valley winds are basically absent in case FLAT (Sect. 3.1.3). Cases I2–I3 have weaker night-time down-valley winds occurring in a smaller part of the valley volume, and hence the outflow of tracer mass during the night is small. Similar behaviour during the night is seen with the other three tracers as well (Figs. S8–S10).

During the second day, the ventilation occurs mostly in the upper halves of the valleys (Fig. 8a–d). Opposite to the first day, the ventilation from the upper half of the valleys takes place before the lower half. This is likely because on the second day the tracer mass is more spatially distributed in the valleys compared to the first day when the tracers are much more spatially confined due to their small release areas. The cross-valley circulation does still ventilate the tracer mass located near the valley surface, but the dominant feature appears to be the transport by the along-valley circulation and the lateral-boundary-induced convergence at the head of the valley. In the inclined valleys, in which the daytime up-valley winds cover the whole length of the valleys, the tracer mass is lifted at the head of the valley (not shown). Some of the lifted tracer is ventilated out of the valley volume and some enters the down-valley-directed return flow, which is located within the valley volume. In the return flow the tracer mass, now transported down-valley above the CBL_v, encounters the upper half of the valley ridge height before the lower half, which is the reason for the ventilation at the upper half taking place before the lower half on the second day.

The vertical fluxes are clearly weaker in case SLOPE (Fig. 8e) compared to valley case I2 (Fig. 8c). In case SLOPE, nearly all the transport of tracers out of the reference volume occurs on the second day. The transport occurs when the tracer plume reaches the end of the domain and is transported out of the analysis volume by the return flow (not shown). Also on the first day, some of the tracer mass makes it up to the return flow, but the return flow is located below the reference height (discussed in Sect. 3.1); hence, the tracer mass does not leave the analysis volume. The cross-valley circulation is very important for bringing the tracer up to the ridge height in the valley cases; this explains the drastic difference in the fluxes between case I2 and case SLOPE, which does not have a cross-valley circulation.

Figure 9 shows the flux components F1–F3 integrated over the whole simulation period for each tracer and case. For tracers 1 and 4 the relative total quantity of ventilated tracers (F2 + F3) does not depend strongly on the valley inclination (Fig. 9a and d). For tracers 2 and 3 the difference is already large, with an increase from 51 % (FLAT) to 65 % (I3) for tracer 2 (Fig. 9b) and from 49 % (FLAT) to 75 % (I3) for tracer 3 (Fig. 9c). Whether the ventilation occurs more by F2 or F3 depends heavily on the tracer release location. An important factor in the vertical fluxes is that the ventilation altitude changes between the valleys. Based on the valley topographies, in case FLAT the ventilation always occurs at 2 km altitude (constant ridge height) for both F2 and F3. In the steepest case, case I3, the ventilation in F2 occurs between 2 and 4 km and in F3 between 4 and 6 km altitude. This has a significant role in where the ventilated tracers end up in the atmosphere.

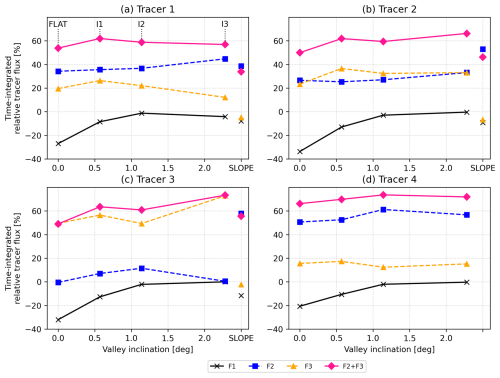
Figure 9 Time integral of the flux components F1–F3 over the whole simulation period for each tracer (a–d) and simulation (valley inclination on the x axis). Case SLOPE is plotted on the right-hand side of each panel.

The outflow of tracers at the valley entrance decreases with increasing inclination (Fig. 9). This is seen as a decrease in the magnitude of the negative F1 with increasing inclination. This is likely due the weakening night-time down-valley winds and the further penetration of the daytime up-valley winds with the increasing valley inclination (Sect. 3.1.5). Although the surface-based down-valley winds are the weakest for case FLAT, the elevated return flow in the residual layer is strong, especially at the valley entrance. Case FLAT has the strongest night-time outflow of tracers at the valley entrance and the shortest along-valley penetration of the up-valley winds. The up-valley winds do not carry the tracer mass as far into the valley as in the inclined cases I1 and I2. In case I3 the night-time down-valley winds are weak, so the night-time horizontal export of tracer mass is seen only for the tracer 1, which is released closest to the valley entrance (Fig. 9a).

3.2.3 Tracer mass distribution in the domain

Figure 10 shows the tracer mass distribution in five sectors during the last hour of the simulations. These sectors are the following:

• 2 km deep surface-based layer above the plain, shown in blue in Fig. 10 (z≤2 km, y<0 km);

• the valley volume, shown in dark grey ($\left|x\right|\le \mathrm{10}$ km, y≥0 km, below ridge height);

• the parallel valley, shown in light grey ($\left|x\right|>\mathrm{10}$ km, y≥0 km, below ridge height);

• the rest of the domain above the valley, shown in orange (y>0 km, above ridge height); and

• the rest of the domain higher than 2 km above the plain, shown in yellow (z>2 km, y<0 km).

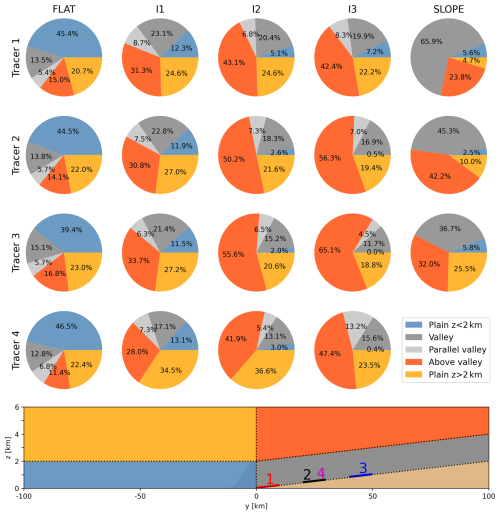
Figure 10 Tracer mass distribution for the shown sectors in the last hour of the simulations. For the valley topographies the sectors “Valley” and “Above valley” are separated by the ridge height (topography I2 shown). For case SLOPE the “Valley” and “Above valley” sectors are separated at 2 km above the surface. The sector “Parallel valley” is the remaining part of the domain for the valley simulations at $\left|x\right|>\mathrm{10}$ km. Numbers 1–4 in the bottom panel denote the along-valley emission location for the tracers.

For all tracers, the inclined valleys transport a larger share of the tracer mass to the two highest sectors (orange and yellow) compared to case FLAT (Fig. 10). Tracers 2 and 3, which are ventilated more from the upper half of the valley atmosphere, result in an increased tracer mass at higher sectors with increasing inclination. Compared to FLAT, in which only about 35 % to 40 % of the tracers end up far above the surface, between 50 % and more than 80 % end up there in the case of inclined valley floors. Although the fluxes F2 and F3 did not depend strongly on the inclination for tracer 1, the relative tracer mass in the two higher sectors is increased for inclined cases (Fig. 10). This is also true for the tracers that were mostly ventilated in the lower half of the valley in the steepest case, case I3, since the ridge height rises up to 4 km by the half-way point of the valley.

For the inclined valleys in cases I1–I3, the tracer mass remaining in the valleys (dark grey shading, Fig. 10) is higher than near the surface above the plain (blue shading). The opposite is found for case FLAT, in which the near-surface sector at the plain gathers the most tracer mass. This is explained by the strongest night-time outflow of the tracer mass to the plain at the valley entrance in case FLAT. The inclined cases accumulate a similar amount of tracer mass within the valley volume when compared together. Although more of the tracer mass stays within the valley volume in the inclined valleys, the remaining tracer mass is located at a higher altitude compared to case FLAT (not shown). Hence, the accumulated tracer mass would have the potential to be ventilated at higher altitudes if the simulation was continued further. For example, in case I3 all of tracer 3 is located above 3 km height at the end of the simulation (not shown). The tracer mass from the plain would also keep ventilating in case FLAT, but the ventilation always occurs at 2 km height.

The transport of tracer mass out of the analysis volume in SLOPE (2 km deep layer above the sloped surface) is much weaker compared to valley simulation I2. The amount of tracer mass in the two highest sector volumes (yellow and orange in Fig. 10) is less than what is simulated in I2, and at least 35 % up to over 65 % of the tracer mass is accumulated in the 2 km deep analysis volume (grey in Fig. 10).

4 Discussion

In this section we attempt to explain the differences in the valley winds and tracer transport between the simulated cases. Results of this study are compared to previous publications and new insights of the study are highlighted.

Our study fills the gap between two previous publications, Wagner et al. (2015a) and Mikkola et al. (2023), both of which studied the effects of the valley floor inclination on the daytime up-valley winds. Similarities were found with both studies despite the fact that the valley topographies differed considerably in these two previous studies and consequently they reached opposite conclusions on how the valley floor inclination effects the daytime up-valley winds (introduced in Sect. 1). Wagner et al. (2015a) found an increase in the valley-averaged along-valley wind speed with increased valley floor inclination, which agrees with our simulations when only considering the range of valley inclinations included in their study. The steepest valley floor inclination in Wagner et al. (2015a) is 0.86°, which sits between the inclination of cases I1 (0.57°) and I2 (1.14°) in our idealised experiments. We found the maximum daytime up-valley wind strength for case I1 and weaker winds for the steeper cases I2 and I3 (2.28°). Wagner et al. (2015a) found that the daytime up-valley wind maximum was located further into the valleys with inclined valley floors when compared to their flat-floored valley. Similarly, in our simulations case FLAT has a valley entrance jet (Sect. 3.1) and weak up-valley winds in the interior of the valley. In the inclined cases the up-valley winds are stronger further in the valleys. In order to form prominent up-valley winds far away from the valley entrance, the valley has to exhibit either (local or regional) inhomogeneities such as changing valley cross-valley shape (for example due to narrowing; Wagner et al., 2015a) or an inclination in the valley floor.

The main difference in our idealised topographies to those studied by Wagner et al. (2015a) is the constant cross-sectional area (shape) along the valley. In Wagner et al. (2015a), the ridges have a constant height of 1.5 km, and hence the valley floor inclination leads to a reduced valley volume along the valley, which is not the case for our simulations with the constant cross-valley shape throughout the valley. In our case the valley volume is the same in all valley simulations and is thus also the topographic amplification factor (TAF) in its traditional form based on the volume ratio. Hence, the traditional TAF does not scale with the strength of the up-valley winds in the inclined valleys of our simulations. The reason for this might be the decreased depth of the up-valley wind layer in the inclined valleys. The up-valley wind layer depth decreases considerably when the valley cross-section reaches above the altitude of CBL_p. For example, in the steepest case, case I3, on the first day of the simulation this point is reached around the half-way point of the valley (Sect. 3.1.1). The shallower CBL_v further in the inclined valleys compared to the valley entrance and shallower CBL_v with increasing valley inclination could be explained by Eq. (5) in Vergeiner and Dreiseitl (1987). They describe the mass flux in up-slope flows, which can be applied to the along-valley winds in our simulations with the inclined valleys. The mass flux decreases with increased background stability and inclination. Close to the valley entrance the background stability for the anabatic up-valley winds is the near-neutral CBL_p, whereas further up in the valley located above the altitude of CBL_p the background environment is the stably stratified atmosphere. Comparison within the inclined valleys is rather simple; steeper valley inclination yields decreased along-valley mass flux (Vergeiner and Dreiseitl, 1987) and hence shallower and weaker up-valley winds in our case. Further in the inclined valleys where the CBL_v is shallower, the portion of cross-valley up-slope winds flowing outside of the CBL_v increases. This also means that a larger share of the heat provided from the valley surface is likely not driving the up-valley winds by the valley volume effect. This would also explain why TAF does not scale with the up-valley wind speeds within the inclined valleys, as the TAF argument is based on negligible heat export out of the valley volume. In this way the steep valley inclination likely shifts the driving mechanism of the up-valley winds from the valley volume effect to the buoyancy forcing instead of combining these two. Far in the valley, above the altitude of CBL_p, the up-valley winds resemble anabatic winds driven by the buoyancy forcing due to the heated sloped surface.

Our steepest valley case, case I3, has approximately the same inclination in the valley floor and ridges as the steeply inclined (2–5°) Himalayan valleys studied in Mikkola et al. (2023). Our finding of decreasing up-valley wind strength and depth with increasing valley inclination supports the findings of Mikkola et al. (2023). The valley inclinations in Mikkola et al. (2023) are much steeper than considered in Wagner et al. (2015a), which caused the conflict in the results of these two studies. In the steep Himalayan valleys above the altitude of the CBL_p, the up-valley winds flow in a shallow layer, which is seen also in our simulations.

The optimal angle for strengthening the up-valley winds is probably determined by the valley geometry, CBL_p depth, and background stability. The valley ridge height, inclination, and CBL_p depth would determine how large a share of the valley volume is characterised by (1) the shallower anabatic up-valley winds flowing above the CBL_p or (2) the anabatic up-valley winds flowing below the CBL_p acting together with the valley-volume-effect-driven up-valley winds with enhancing impact. Valley inclination and the stability of the atmosphere above the up-valley wind layer would influence the buoyant forcing of the along-valley winds, affecting the strength and depth of the anabatic up-valley winds.

The inclined valleys were found to have daytime vertically stacked circulation in the along-valley direction (Sect. 3.1.1). Such stacked circulation cells have previously been found only in the cross-valley circulation, but in the along-valley direction this type of stacked circulation has not been documented in previous publications. The weak secondary cell above the main valley circulation is likely being dominated easily by the background flow or pressure gradients, which do not exist in our simulations. This would explain the lack of published observational or modelling studies referring to this flow feature in real valleys. The authors are not aware of previous idealised studies with similar inclined valley topographies, which is suggested to be the crucial topographic feature for forming this stacked circulation in the along-valley direction.

Similar to the passive tracers in our simulations the parcels from the valley entrance were transported faster into the valley with an inclined valley floor in Wagner et al. (2015a) when compared to the flat-floored valley. This occurs due to the higher wind speeds in the inclined valleys (Wagner et al., 2015a) but also probably due to the further along-valley spread of the up-valley winds. Also in their simulations the transport out of the valley occurs closer to the valley entrance for the flat-floored valley, similar to our case FLAT. Also the transport to the plain by the return flow was weaker for the valley with an inclined valley floor. This is probably due to the further transport of the tracers during daytime and weaker down-valley winds during the night. In the case of Wagner et al. (2015a) the ventilation occurred at the same height for each of the valleys, so the valley floor inclination did not change the final height distribution of the tracer mass as it did in our simulations. In our case, the tracer ventilation occurs at higher altitudes with increasing inclination. The tracers are transported by the up-valley winds before they exit the valley volume at the upper lid of the valley volume, which means that the tracer mass is lifted in the vertical direction prior to the ventilation and the ventilation occurs at higher altitude.

Although the along-slope winds in case SLOPE were not that different to the along-valley winds in case I2 with the same inclination, the transport of tracers differs a lot. Transport of tracers out from the 2 km deep layer above the sloped surface was much weaker than the transport out of the valley volume in case I2. The cross-valley circulation bringing the tracer to the ridge height is crucial in the ventilation, rather than the along-valley winds that have a more or less similar magnitude as the along-slope winds in case SLOPE. This highlights the importance of the vertical transport by mean cross-valley circulation for accurate representation of the mountain ventilation that needs to be either resolved or parameterised. Coarse resolution could resolve the mean winds and the along-valley transport with decent accuracy when considering only the inclination, but the transport processes are not simulated properly without resolving the cross-valley circulation in the valley.

Bianchi et al. (2021) suggested that the valleys at the southern slope of the Himalayan mountain range act as sources of free-tropospheric aerosol. The daytime up-valley winds were proposed to bring the aerosol up to the high elevation of 5 km within the valley volume before the ventilation takes place. Wind comparison of four Himalayan valleys in Mikkola et al. (2023) supported this hypothesis as the other valleys also had up-valley winds reaching to these high altitudes within the valleys. Our simulations show the inclined valleys, like the Himalayan valleys studied by Bianchi et al. (2021) and Mikkola et al. (2023), to be efficient in transporting tracer mass from the low elevations of the valleys up to high elevations in the free troposphere. In our simulations the steepest valley ventilated the tracers to the highest level in the atmosphere (Sect. 3.2.3). Ventilation to the high elevations favours long-range transport and a longer lifetime for the aerosol, with higher potential for climate impact in the free troposphere.

So far, we have investigated the impact of valley inclination with only one combination of the surface sensible heat flux and initial temperature profile. Different combinations of the surface heating, valley inclination, and initial stability could reveal more details on which features are the most important in determining the optimal angle for strengthening the daytime up-valley winds. The lateral boundary conditions in the along-valley direction define how the up-valley flow behaves at the head of the valleys. This is especially prominent in the inclined valleys which show well-defined up-valley winds for whole length of the valleys and develop strong return flow at the head of the valley due the forced convergence near the domain boundary. This resembles a mountain ridge where an identical valley would oppose the flow at the head of the valley (not taking into account the effects of the south–north orientation on the thermally driven winds). A larger domain with a plateau following the head of the valley would better resemble the Himalayan valleys studied in Mikkola et al. (2023) and could give interesting insights for the transport of the tracers into the free troposphere but also through the valley. These Himalayan valleys open up to the Tibetan Plateau at the head of the valleys, and in the idealised simulations this would allow lateral transport through the valley in addition to the lateral transport at the valley entrance and vertical transport at the upper lid of the valley. However, this would substantially increase the computational requirements of the simulations. The night-time surface-based down-valley winds are likely sensitive to the surface cooling, which is in our simulations is constant at −10 W m⁻². With stronger night-time cooling, the surface-based down-valley wind layer could grow in height, making the residual layer up-valley winds a less dominant feature.

5 Conclusions

We study the effects of valley inclination on the valley winds and transport of passive tracers using high-resolution WRF simulations. Four idealised valley topographies with differing valley inclinations and one experiment with a flat slope were simulated. The focus of the analysis is on the along-valley winds and transport of passive tracers out of the valley volume. The key findings are as follows.

• The valley inclination allows daytime up-valley winds to penetrate further into the valley compared to a flat-floored valley where strong winds are limited to the entrance. Additionally, steeper inclinations strengthen daytime up-valley winds, but only up to a certain point. Beyond that critical angle, the winds weaken again.

• The flat-floored valley has the strongest average night-time down-valley winds, although the surface-based down-valley winds are prominent only in the inclined valleys. The night-time residual layer within the valley volume is characterised by up-valley winds and return flow, which weaken with increasing valley inclination.

• Inclined valleys allow daytime winds to carry passive tracers deeper into the valley before they are ventilated out of the valley. Consequently, this ventilation occurs in steeper valleys at a higher altitude than for the flat-floored valley.

• The flat-floored valley exhibits stronger overall tracer outflow compared to inclined valleys. However, this higher outflow occurs at lower altitude due to the lower crest height. This confines the majority of the ventilated tracers to the lowest few kilometres of the atmosphere. Therefore, steep valleys are more efficient in ventilating tracers to the upper troposphere, where long-range transport can take place.

An increased number of experiments with differing valley shapes, initial profiles of temperature, and surface heating could give more insights on the controlling factors which define the optimal angle of strengthening the daytime up-valley winds. Future studies could incorporate physical and chemical modelling of aerosol processes instead of passive tracers with an idealised valley setup. The coupled effects of aerosol population within the valley atmosphere and the valley winds, and hence the transport of aerosol, could be studied using idealised valley topographies. Realistic surface emission, aerosol removal, and production processes could reveal insights in what happens to the aerosol prior to the ventilation out of the valley.

Appendix A: Data analysis equations

A1 Valley winds

A1.1 Figure 5

Valley-volume-averaged along-valley wind shown in Fig. 5a is a spatial average of the y wind computed using the formula

$$\begin{array}{}\text{(A1)}& v_{\text{mean}}\left(t\right)={\displaystyle \frac{{\int }_{-S_x}^{S_x}{\int }_{\mathrm{0}}^{L_y}{\int }_{h(x,y)}^{h_{\mathrm{r}}\left(y\right)}v(t,x,y,z)\mathrm{d}z\mathrm{d}y\mathrm{d}x}{{\int }_{-S_x}^{S_x}{\int }_{\mathrm{0}}^{L_y}{\int }_{h(x,y)}^{h_{\mathrm{r}}\left(y\right)}\mathrm{1}\mathrm{d}z\mathrm{d}y\mathrm{d}x}},\end{array}$$

where S_x is the half-width of the valley, L_y is the length of the valley, h(x,y) is the space-dependent height of the valley topography, h_r(y) is the height of the two ridges in the along-valley direction at $x=\pm S_x$ (see Eqs. 2–4 in Sect. 2.2), and $v(t,x,y,z)$ is the y component of the wind.

Valley-averaged up-valley wind shown in Fig. 5b is a spatial average of the positive y wind and is computed using the formula

$$\begin{array}{}\text{(A2)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{v}_{\text{up-valley}}\left(t\right)=\\ {\displaystyle }& {\displaystyle \frac{{\int }_{-S_x}^{S_x}{\int }_{\mathrm{0}}^{L_y}{\int }_{h(x,y)}^{h_{\mathrm{r}}\left(y\right)}\left(v\right(t,x,y,z\left){\mathrm{1}}_{v(t,x,y,z)>\mathrm{0}}\right)\mathrm{d}z\mathrm{d}y\mathrm{d}x}{{\int }_{-S_x}^{S_x}{\int }_{\mathrm{0}}^{L_y}{\int }_{h(x,y)}^{h_{\mathrm{r}}\left(y\right)}{\mathrm{1}}_{v(t,x,y,z)>\mathrm{0}}\mathrm{d}z\mathrm{d}y\mathrm{d}x}},\end{array}\end{array}$$

where ${\mathrm{1}}_{v(t,x,y,z)>\mathrm{0}}$ is an indicator function taking into account only the grid boxes with up-valley wind.

A1.2 Figure 6

This is a step-by-step derivation of the along-valley-averaged air mass transport, shown in Fig. 6. First, we start with the along-valley-directed horizontal dry air mass flux, $v(t,x,y,z)\cdot {\mathit{\rho }}_{\mathrm{d}}(t,x,y,z)$, which has the unit of $\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}\mathrm{kg}{\mathrm{m}}^{-\mathrm{3}}$. v is the y component of the wind and ρ_d is the dry air density. Next we integrate the dry air mass flux over each valley cross-section in the x–z plane, which we denote by A(t,y):

$$A(t,y)=\underset{-S_x}{\overset{S_x}{\int }}\underset{h(x,y)}{\overset{h_{\mathrm{r}}\left(y\right)}{\int }}\left(v\right(t,x,y,z\left){\mathit{\rho }}_{\mathrm{d}}\right(t,x,y,z\left)\right)\mathrm{d}z\mathrm{d}x,$$

which has the unit of kg s⁻¹. S_x is the half-width of the valley, h(x,y) is the space-dependent height of the valley topography, and h_r(y) is the height of the two ridges in the along-valley direction at $x=\pm S_x$. Now we take spatial average in the along-valley direction; this results in one value of averaged integrated mass flux in the y direction for each time step, which we denote by B(t):

$$B\left(t\right)={\displaystyle \frac{\mathrm{1}}{L_y}}\underset{\mathrm{0}}{\overset{L_y}{\int }}A(t,y)\mathrm{d}y,$$

where L_y is the length of the valley. Finally, we integrate over the selected time period

$$\underset{t}{\int }B\left(t\right)\mathrm{d}t$$

and end up with the along-valley-averaged air mass transport, which has the unit of kilograms (kg).

For the case SLOPE the derivation is otherwise the same as presented above for the valley cases but the integration boundaries differ. In the x direction the reference volume covers the entire domain and in the z direction the upper boundary is the reference height 2 km, corresponding to the ridge height in the valley simulations. Since the area of the x–z plane for integration is 4 times larger than in the valley cases, the values of SLOPE are divided by 4 for comparable values.

A2 Tracer transport

All the analysed variables in the tracer analysis are normalised by the total tracer mass in the domain. The total mass of the tracer i in the model domain at time step t, denoted by M_i,tot(t), is computed using the formula

$$\begin{array}{}\text{(A3)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{M}_{i,\text{tot}}\left(t\right)=\\ {\displaystyle }& {\displaystyle }{\int }_{-\mathrm{20}\text{km}}^{\mathrm{20}\text{km}}{\int }_{-\mathrm{100}\text{km}}^{\mathrm{100}\text{km}}{\int }_{\mathrm{0}}^{\mathrm{20}\text{km}}{\text{TR}}_i(t,x,y,z){\mathit{\rho }}_{\mathrm{d}}(t,x,y,z)\mathrm{d}z\mathrm{d}y\mathrm{d}x,\end{array}\end{array}$$

where TR_i is the mixing ratio of the tracer i and ρ_d is the dry air density.

For the case SLOPE the tracer analysis equations are otherwise the same as presented below for the valley cases but the integration boundaries differ. In the x direction the reference volume covers the entire domain and in the z direction the upper boundary is the reference height 2 km, corresponding to the ridge height in the valley simulations.

A2.1 Figure 7

The relative tracer mass in the valley volume shown in Fig. 7, which has the unit of kg kg⁻¹, is computed using the formula

$$\begin{array}{}\text{(A4)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{m}_{i,\text{valley}}\left(t\right)=\\ {\displaystyle }& {\displaystyle \frac{{\int }_{-S_x}^{S_x}{\int }_{\mathrm{0}}^{L_y}{\int }_{h(x,y)}^{h_{\mathrm{r}}\left(y\right)}{\text{TR}}_i(t,x,y,z){\mathit{\rho }}_{\mathrm{d}}(t,x,y,z)\mathrm{d}z\mathrm{d}y\mathrm{d}x}{M_{i,\text{tot}}\left(t\right)}},\end{array}\end{array}$$

where S_x is the half-width of the valley, L_y is the length of the valley, h(x,y) is the space-dependent height of the valley topography, and h_r(y) is the height of the two ridges in the along-valley direction at $x=\pm S_x$ (see Eqs. 2–4 in Sect. 2.2).

A2.2 Figures 8 and 9

Relative tracer mass fluxes out of the valley volume, which have the unit of $\mathrm{kg}{\mathrm{kg}}^{-\mathrm{1}}{\mathrm{h}}^{-\mathrm{1}}$, are shown in Fig. 8. See Fig. 2 as a reference for the fluxes F1–F3. In Eqs. (A5)–(A7), f_y,i and f_z,i denote the total mass flux of tracer i in the y and z directions, respectively. The total flux is the sum of the resolved and sub-grid-scale fluxes. The horizontal tracer mass flux of tracer i at the valley entrance, denoted by F1, is given by

$$\begin{array}{}\text{(A5)}& {\text{F1}}_i\left(t\right)={\displaystyle \frac{{\int }_{-S_x}^{S_x}{\int }_{h(x,y=\mathrm{0})}^{h_{\mathrm{r}}(y=\mathrm{0})}\left(f_{y,i}\right(t,x,y=\mathrm{0},z\left)\right)\mathrm{d}z\mathrm{d}x}{M_{i,\text{tot}}\left(t\right)}}.\end{array}$$

The tracer mass fluxes of tracer i normal to the valley inclination at the ridge height, i.e. the flux out at the upper lid of the valley volume, divided into F2 and F3 corresponding to the lower half and upper half of the valley are respectively given by

$$\begin{array}{}\text{(A6)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{\text{F2}}_i\left(t\right)=\\ {\displaystyle }& {\displaystyle \frac{{\int }_{-S_x}^{S_x}{\int }_{\mathrm{0}}^{L_y/\mathrm{2}}\left(\begin{array}{l}\frac{L_y}{\sqrt{L_y^{\mathrm{2}}+H_{\mathrm{e}}^{\mathrm{2}}}}{f}_{z,i}(t,x,y,z=h_{\mathrm{r}}(y\left)\right)\\ +\frac{H_{\mathrm{e}}}{\sqrt{L_y^{\mathrm{2}}+H_{\mathrm{e}}^{\mathrm{2}}}}{f}_{y,i}(t,x,y,z=h_{\mathrm{r}}(y\left)\right)\end{array}\right)\mathrm{d}y\mathrm{d}x}{M_{i,\text{tot}}\left(t\right)}}\end{array}\end{array}$$

and

$$\begin{array}{}\text{(A7)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{\text{F3}}_i\left(t\right)=\\ {\displaystyle }& {\displaystyle \frac{{\int }_{-S_x}^{S_x}{\int }_{L_y/\mathrm{2}}^{L_y}\left(\begin{array}{l}\frac{L_y}{\sqrt{L_y^{\mathrm{2}}+H_{\mathrm{e}}^{\mathrm{2}}}}{f}_{z,i}(t,x,y,z=h_{\mathrm{r}}(y\left)\right)\\ +\frac{H_{\mathrm{e}}}{\sqrt{L_y^{\mathrm{2}}+H_{\mathrm{e}}^{\mathrm{2}}}}{f}_{y,i}(t,x,y,z=h_{\mathrm{r}}(y\left)\right)\end{array}\right)\mathrm{d}y\mathrm{d}x}{M_{i,\text{tot}}\left(t\right)}},\end{array}\end{array}$$

where H_e is the height of the valley floor at the end of the valley, i.e. the elevation gain of the valley topography along the valley length.

Figure 9 shows the time integral of F1_i(t), F2_i(t), and F3_i(t) over the whole simulation period, which results as the share of the tracer mass transported across F1–F3 during the simulation; this has the unit of $\mathrm{kg}{\mathrm{kg}}^{-\mathrm{1}}\mathrm{h}{\mathrm{h}}^{-\mathrm{1}}$ and is presented as a percentage.

A2.3 Figure 10

Tracer mass distribution in the model domain during the last hour of the simulation is shown in Fig. 10. The tracer mass of tracer i in each sector is a spatial integral given by

$$\begin{array}{}\text{(A8)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{m}_{i,\text{sector}}=\\ {\displaystyle }& {\displaystyle }\underset{x}{\int }\underset{y}{\int }\underset{z}{\int }{\text{TR}}_i(t=\mathrm{48}\mathrm{h},x,y,z){\mathit{\rho }}_{\mathrm{d}}(t=\mathrm{48}\mathrm{h},x,y,z)\mathrm{d}z\mathrm{d}y\mathrm{d}x.\end{array}\end{array}$$

The integration boundaries for each sector can be found in Sect. 3.2.3.