Impact of host climate model on contrail cirrus effective radiative forcing estimates

Estimates of aviation effective radiative forcing (ERF) indicate that contrail cirrus is currently its largest contributor, although with a substantial associated uncertainty of ∼ 70 %. Here, we implement the contrail parameterisation developed for the Community Atmosphere Model (CAM) in the UK Met Office Unified Model (UM), allowing us to compare, for the first time, the impact of key features of the host climate model on contrail cirrus ERF. We find that differences in background humidity between the models result in the UM-simulated contrail fractions being 2 to 3 times larger than in CAM. Additionally, the models show contrasting responses in overall global cloud fraction, with contrails increasing the total cloud fraction in the UM and decreasing it in CAM. Differences in the complexity of the cloud microphysics schemes lead to significant differences in simulated changes to cloud ice water content due to aviation. After compensating for the unrealistically low contrail optical depth in the UM, we estimate the 2018 contrail cirrus ERF to be 40.8 mW m⁻² in the UM, compared to 60.1 mW m⁻² in CAM. These values highlight the substantial uncertainty in contrail cirrus ERF due to differences in microphysics and radiation schemes between the two models. We also find a factor-of-8 uncertainty in contrail cirrus ERF due to existing uncertainty in contrail cirrus optical depth. Future research should focus on better representing microphysical and radiative contrail characteristics in climate models and on improved observational constraints.

1 Introduction

The aviation sector has been growing rapidly over the last 6 decades, except for a temporary decrease in traffic caused by the measures to limit the spread of the COVID-19 pandemic (ICAO, 2024a). The steady growth of civil aviation has resulted in an average increase in carbon dioxide (CO₂) emissions of 2 % yr⁻¹ between 1970 and 2012, further accelerating to 5 % yr⁻¹ from 2013 to 2018 (Lee et al., 2021). According to the International Civil Aviation Organization (ICAO) monthly monitor, passenger air traffic on most routes had reached the pre-pandemic revenue passenger kilometre (RPK) level by the end of 2023 (ICAO, 2024b). Furthermore, predictions based on various economic and future aircraft emission scenarios estimate that aviation fuel usage and associated CO₂ emissions could experience 2–3-fold increases by 2050 (Dray et al., 2022).

As recently reviewed by Lee et al. (2021), global aviation in 2018 contributed 3.5 % to the total anthropogenic effective radiative forcing (ERF). While a third of the aviation ERF is estimated to be caused by CO₂ emissions, the majority (i.e. two-thirds) is associated with non-CO₂ effects, including aviation-induced cloudiness (contrails and contrail cirrus) and emissions of nitrogen oxides (NO_x), water vapour, and aerosols (in particular, soot, and sulfate). Of the known aviation climate forcing contributors, contrails and contrail cirrus (i.e. spreading contrails that are no longer line-shaped) are estimated to be the largest, responsible for almost twice as much as the CO₂ contribution (Burkhardt and Kärcher, 2011). Contrails are line-shaped high clouds that form as a result of the mixing between the warm and moist jet engine exhaust and the cool ambient air under liquid water saturation conditions in the young plume behind the aircraft (Schumann, 1996). Schmidt (1941) and Appleman (1953) described the contrail formation process based on the thermodynamic theory. At present, water vapour primarily condenses on particles emitted by today's kerosene combusting engines. However, these emitted particles are not necessary at the contrail formation stage as particles from the ambient air could be entrained into the exhaust plume and act as condensation nuclei. When the ambient air is supersaturated with respect to ice, contrails can persist and may last from minutes up to several hours (Minnis et al., 1998). Persistent contrails may evolve into extended cirrus clouds (i.e. contrail cirrus) due to spreading and shearing (Kärcher, 2018).

Like natural cirrus, contrail cirrus clouds change the radiative balance of Earth in two ways. First, their ice crystals can scatter shortwave radiation back to space, leading to a reduction in solar radiation reaching the Earth's surface (shortwave cooling effect). Second, contrails absorb infrared (longwave) radiation from Earth and re-emit it at lower temperatures (longwave warming effect). For contrails, the longwave warming effect dominates on average, causing a net positive (warming) radiative forcing (RF) (Burkhardt and Kärcher, 2011; Rap et al., 2010a; Chen and Gettelman, 2013). Contrail cirrus can also have an impact on natural clouds as their presence changes the water budget of the surrounding atmosphere. This may partially offset the direct climate impact of contrail cirrus (Burkhardt and Kärcher, 2011) and therefore reduce the contrail cirrus climate efficacy (Bickel, 2023).

The global climate impact from aviation, including contrails and contrail cirrus, has been reviewed over the past decades. Initial assessments (e.g. Minnis et al.,1999; Lee et al., 2009) only considered the effect of linear contrails. Simulating and quantifying the effect of ageing and spreading contrails is challenging for models as this requires simulating the whole contrail cirrus life cycle, including complex cloud microphysical processes, spreading, and the interaction with background cloudiness (Burkhardt and Kärcher, 2009). A best estimate for contrail cirrus ERF (including the natural cloud feedback) was only available in the latest two Intergovernmental Panel on Climate Change (IPCC) Assessment Reports (ARs), i.e. Boucher et al. (2013) and Lee et al. (2021). In the IPCC Fifth AR, the ERF of contrail cirrus was estimated for 2011 as 50 mW m⁻² (5 %–95 % likelihood range of [20, 150]) (Boucher et al., 2013). This was derived from scaling and averaging two studies, i.e. Schumann and Graf (2013) and Burkhardt and Kärcher (2011). More recently, Lee et al. (2021) provided estimates of contrail cirrus ERF of 57 mW m⁻² (5 %–95 % likelihood range of [17, 98]) for 2018, calculated by scaling and averaging updated contrail cirrus RF and ERF estimates (Bock and Burkhardt, 2016; Burkhardt and Kärcher, 2011; Chen and Gettelman, 2013; Bickel et al., 2020; Schumann et al., 2015). Therefore, in the IPCC Sixth AR, the uncertainty in the contrail cirrus ERF has been reduced compared with the IPCC Fifth AR to 70 % due to the development of process-based approaches simulating contrail cirrus in recent years. However, this uncertainty remains large, with low confidence in the current best estimates of contrail cirrus ERF, reflecting the incomplete knowledge of key factors, such as the contrail spreading rate, optical depth, and radiative transfer processes (Lee et al., 2021). The 70 % uncertainty results from the combined process uncertainties, simulated in a small number of available studies (Lee et al., 2021). There are three main sources of this uncertainty: (i) upper-tropospheric humidity and clouds, which largely originates from the high variability in the temporal and spatial scales of upper-tropospheric ice supersaturation; (ii) the treatment of contrail cirrus and the interactions with natural clouds, in particular the contrail ice crystal microphysical properties, contrail cirrus life cycle, and natural cloud adjustments; (iii) the radiative transfer response to contrail cirrus, which is largely due to differences in the radiation schemes across climate models, background cloud fields and their vertical overlap with contrail cirrus, homogeneity assumptions of the contrail cirrus field, and the presence of very small ice crystals and unknown ice crystal habits. In addition to this 70 % quantified uncertainty, there is also the unquantified uncertainty due to the impact of contrails forming within natural clouds or the change in radiative transfer due to soot aerosols in contrail cirrus ice crystals.

The aviation industry has been under increasing pressure in recent years to substantially reduce its climate effect. Contrail cirrus is currently the largest aviation short-lived climate forcer and is therefore an important target for mitigation, which would make an immediate impact on the Earth's radiation budget. The decreases in the contrail occurrence and contrail cirrus ERF due to the reduction in air traffic resulting from pandemic restrictions in early 2020 have been demonstrated in several modelling and observation-based studies (Quaas et al., 2021; Digby et al., 2021; Schumann et al., 2021; Gettelman et al., 2021). A number of mitigation options have been explored to reach the aviation industry's commitment of achieving net-zero CO₂ emissions by 2050, including technical improvements, operational management, and the use of alternative fuels (IATA, 2025). However, the large uncertainties in and poor scientific understanding of the contrail climate forcing could undermine the effectiveness of these mitigation strategies and create unintended consequences of increasing the overall climate forcing.

To date, there have only been two global climate models able to simulate contrail cirrus, i.e. ECHAM (Burkhardt and Kärcher, 2009; Burkhardt and Kärcher, 2011) and the NCAR (National Center for Atmospheric Research) Community Atmosphere Model (CAM) (Chen et al., 2012; Chen and Gettelman, 2013). These models include different physical parameterisations for cloud microphysics in general and contrail cirrus parameterisations in particular, with ECHAM simulating a separate contrail cirrus cloud class and CAM integrating contrail ice with other ice clouds. This limits our ability to constrain the contrail cirrus ERF uncertainty.

In this study, we perform the first comparison of a contrail cirrus scheme across two global climate models (GCMs), each in its respective standard configuration. The main aim is to investigate the impact of key host climate model characteristics on contrail cirrus simulations by adapting the Chen et al. (2012) contrail cirrus CAM parameterisation for the UK Met Office Unified Model (UM) (Sellar et al., 2019). Using the same contrail parameterisation in two different host climate models, we are able to directly compare contrail cirrus estimates and therefore contribute to improving our understanding of main sources of uncertainty in simulated contrail cirrus microphysical and optical properties, as well as the associated natural cloud responses.

This paper is organised as follows: Sect. 2 provides descriptions of the UM and CAM models, the contrail parameterisation, and the model setups used for the contrail simulations. Section 3 presents and analyses the simulated differences in ice supersaturation frequency, young-contrail properties, cloud and radiation responses, and ERF estimates between the two climate models. The summary and conclusions are provided in Sect. 4.

2 Methodology

2.1 The host climate models

In this study, contrail cirrus simulations were performed with two atmospheric models: the UM and CAM. Despite their different cloud microphysics and radiation schemes, both the UM and CAM compare well with satellite observations in terms of simulated cloud microphysical, macrophysical, and optical properties (e.g. ice and liquid water path and specific humidity) (Jiang et al., 2012; Medeiros et al., 2023; Vignesh et al., 2020; Delanoë et al., 2011; Williams and Bodas-Salcedo, 2017).

The UM is a numerical model of the atmosphere which is used for both weather and climate applications. The UM is coupled as the atmospheric component of past and current generations of the UK climate models, i.e. the Hadley Centre Coupled Model (HadCM), the Hadley Centre Global Environmental Model (HadGEM), and the UK Earth System Model (UKESM), which are part of the Climate Model Intercomparison Project (CMIP) and have provided input to the IPCC ARs over the years. Cloud microphysics in the UM is parameterised by the Wilson and Ballard (1999) one-moment large-scale precipitation scheme, with extensive modifications. For instance, ice cloud parameterisations use the universal particle size distribution (PSD) of Field et al. (2007) built on a large quantity of in situ-measured PSDs and mass–diameter relations of Cotton et al. (2013). The cloud fraction and condensate are addressed by the PC2 large-scale cloud scheme of Wilson et al. (2008). The impact of convective cloudiness is represented by source terms that couple the convection scheme to PC2, based on Tiedtke (1993) and Wilson et al. (2008). In-cloud supersaturation is permitted by the model and is diagnosed by the parameterisation described in Furtado and Field (2017). The parameterisation assumes that the ice cloud fraction in each grid box is partitioned into supersaturated and sub-saturated sub-areas. The areas and relative humidity (RH) of these regions are parameterised in terms of grid-box mean quantities from an assumed sub-grid RH distribution. Additional complexities are introduced to handle mixed-phase and supercool-liquid-only areas. In this scheme, there is no requirement for grid-scale RH over ice to be zero – i.e. depositional growth of ice is handled prognostically, without assuming instantaneous saturation adjustment. Radiative transfer is calculated with the Suite of Community RAdiative Transfer codes based on Edwards and Slingo (SOCRATES) scheme (Edwards and Slingo, 1996; Manners, 2025), using six shortwave and nine longwave radiation bands. The radiation scheme treats cloud ice crystals following Baran et al. (2016), assuming a maximum random overlap for the vertical cloud layers.

CAM (Bogenschutz et al., 2018) is the atmospheric component of Community Earth System Model (CESM) (Danabasoglu et al., 2020). CAM version 6 (CAM6), which is used here, employs a double-moment cloud microphysics scheme (Gettelman and Morrison, 2015; Gettelman, 2015) and has been recently updated to include rimed ice (Gettelman et al., 2019). The scheme is coupled to an aerosol microphysics and chemistry model (MAM4; Liu et al., 2016) and driven by a unified turbulence scheme for the boundary layer, shallow convection, and large-scale condensation (Bogenschutz et al., 2013; Larson, 2017). The number concentration of aerosols is connected to ice–warm-cloud microphysics, accounting for ice and liquid activation of cloud crystals and drops (Liu et al., 2016). In CAM6 the convective cloud scheme is based on the description of Zhang and McFarlane (1995) and Zhang et al. (1998). Ice supersaturation is allowed as described by Gettelman et al. (2010, 2015). Saturation adjustment and condensation is performed based on the vapour pressure over liquid. Ice formation occurs only when nucleation conditions are satisfied based on the available ambient aerosols and the ice nucleation scheme of Liu and Penner (2005). Once ice is formed, a vapour deposition process onto ice occurs, as described by Gettelman et al. (2010), and contrails uptake water in the same manner. The model radiation code has been updated to the Rapid Radiative Transfer Model for General Circulation Models (RRTMG) (Iacono et al., 2008). RRTMG divides the solar spectrum into 14 bands and the thermal infrared into 16 bands, with a varying number of quadrature points (g points) in each of the bands. The cloud overlap is treated using the maximum random cloud overlap assumption in RRTMG, similarly to the SOCRATES radiative transfer scheme in the UM.

2.2 The contrail parameterisation

Previous studies have simulated the climate impact of contrails in the UM using a linear contrail scheme (Rap et al., 2010a, b). In order to allow the UM to also simulate the spreading of linear contrails into contrail cirrus and the associated impacts on natural cirrus clouds (Burkhardt and Kärcher, 2011), here we adapt the Chen et al. (2012) CAM contrail cirrus parameterisation for the UM. This contrail parameterisation has been used in several studies on aviation climate impacts (e.g. Chen and Gettelman, 2013; Gettelman et al., 2021; Lee et al., 2021).

In this contrail cirrus parameterisation, contrails form according to the Schmidt–Appleman criterion (Schumann, 1996) and persist in ice-supersaturated regions. An empirical formula giving the critical temperature (T_c, in degrees Celsius) for contrail formation, as described by Schumann (1996), is

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{T}_{\mathrm{c}}=& -\mathrm{46.46}+\mathrm{9.43}\ln (G-\mathrm{0.053})\\ & +\mathrm{0.72}{\left[\ln (G-\mathrm{0.053})\right]}^{\mathrm{2}},\end{array}\end{array}$$

with G, in units of Pa K⁻¹, defined as

$$\begin{array}{}\text{(2)}& G={\displaystyle \frac{{\mathrm{EI}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\cdot c_{p}p}{\mathit{\epsilon }Q\left(\mathrm{1}-\mathit{\eta }\right)}},\end{array}$$

where ${\mathrm{EI}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is the emission index of water vapour in kg${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ kg${}_{\mathrm{fuel}}^{-\mathrm{1}}$, c_p is the specific heat of air at constant pressure in J kg${}_{\mathrm{air}}^{-\mathrm{1}}$ K⁻¹, p is the atmospheric pressure in pascals (Pa), ε is the ratio of molecular masses of water and air in (kg${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ mol⁻¹) (kg_air mol⁻¹)⁻¹, Q is the specific combustion heat in J kg${}_{\mathrm{fuel}}^{-\mathrm{1}}$, and η is the propulsion efficiency of the jet engine.

The critical relative humidity RH_c for contrail formation depends on G, T_c, and the ambient temperature T and is expressed, as in Ponater et al. (2002), as

$$\begin{array}{}\text{(3)}& {\mathrm{RH}}_{\mathrm{c}}\left(T\right)={\displaystyle \frac{G\cdot \left(T-T_{\mathrm{c}}\right)+e_{\mathrm{sat}}^{\mathrm{L}}\left(T_{\mathrm{c}}\right)}{e_{\mathrm{sat}}^{\mathrm{L}}\left(T\right)}},\end{array}$$

where $e_{\mathrm{sat}}^{\mathrm{L}}$ is the saturation pressure of water vapour with respect to the liquid phase.

Contrails form when the ambient temperature is below the critical temperature and the ambient relative humidity with respect to liquid water is above the critical relative humidity. Furthermore, a contrail persistence condition requires that the ambient air be supersaturated with respect to ice. In addition to the water vapour emitted by aircraft engines, ambient water vapour above ice saturation within the volume swept by aircraft is also added to the formation of contrails. This aircraft-swept volume is a product of the flight path distance d in metres (m) and cross-sectional area C in square metres (m²) (Chen et al., 2012). The contrail ice mass mixing ratio is therefore calculated as

$$\begin{array}{}\text{(4)}& M=q_{\mathrm{t}}\mathrm{\Delta }t+{\displaystyle \frac{d\cdot C}{V}}\left(x-x_{\mathrm{sat}}^i\right),\end{array}$$

where q_t is the aviation water vapour emission mixing ratio (ratio of the mass of aircraft water vapour emission to the mass of dry air) tendency in kg kg⁻¹ s⁻¹, V is the volume of the given grid cell in cubic metres (m³), x is the ambient specific humidity (ratio of the mass of ambient water vapour to the total mass of air) in kg kg⁻¹, and $x_{\mathrm{sat}}^i$ is the saturation specific humidity with respect to ice under the ambient temperature and pressure in kg kg⁻¹. The contrail fraction is calculated as the ratio of the contrail ice mass mixing ratio and an empirical value for the in-cloud ice water content (ICIWC):

$$\begin{array}{}\text{(5)}& \mathrm{\Delta }A={\displaystyle \frac{M}{\mathrm{ICIWC}/{\mathit{\rho }}_{\mathrm{a}}}},\end{array}$$

where ρ_a is the density of air and ICIWC is calculated as a function of temperature as

$$\begin{array}{}\text{(6)}& \mathrm{ICIWC}\left(\mathrm{g}{\mathrm{m}}^{-\mathrm{3}}\right)=e^{\left(\mathrm{6.97}+\mathrm{0.103}T\left(\mathit{°}\mathrm{C}\right)\right)}\times {\mathrm{10}}^{-\mathrm{3}}.\end{array}$$

The contrail parameterisation is described in detail in Chen et al. (2012), where the contrail model simulation results have been evaluated against observations.

In both host climate models (i.e. the UM and CAM), contrail cirrus and natural clouds compete for water vapour available for deposition and contrails feed back onto natural cirrus cloudiness due to contrail-induced changes in moisture and temperature. If ice supersaturation persists, the contrail cloud will take up ambient water vapour and grow. The subsequent evolution of contrails is determined by the model state, and the contrail cloud is treated no differently than any other ice cloud in the models. The contrail ice mass and fraction are added to the large-scale ice mass and cloud fraction as increments at the end of each time step.

Contrail ice number concentration is treated differently when added to natural clouds due to the different cloud microphysics schemes in the two models. For CAM, this is a double-moment scheme (Gettelman and Morrison, 2015; Gettelman, 2015), where contrails are described by their fraction, ice water mixing ratio, and ice crystal number concentration. In contrast, the UM has a one-moment cloud microphysics scheme (Wilson and Ballard, 1999), where contrails are described by their fraction and ice water mixing ratio only. This means that in the UM, the same prescribed ice number concentration is applied to both natural cirrus and contrails. The effects of the UM one-moment scheme on contrail cirrus simulations are discussed in Sect. 3. By explicitly simulating ice crystal number concentration changes in its double-moment cloud scheme, CAM is able to overcome the contrail optical depth underestimation simulated by one-moment schemes (Kärcher et al., 2010). This underestimation remains an issue that needs to be accounted for in the UM. Another difference between the two climate models consists in the fact that while there are separate ice and snow categories in CAM, there is only one ice category in the UM (containing both ice and snow), represented by a single generic ice distribution based on a large dataset (Field et al., 2007).

In terms of air traffic inventory, we use the Aviation Environmental Design Tool (AEDT) dataset for both our UM and our CAM simulations, including monthly mean distance flown and water vapour emission from air traffic for the year 2006 (Wilkerson et al., 2010). The initialised ice particles within contrails in CAM are assumed to be spherical and have a radius of 3.75 µm based on contrails aged for 20–30 min (Schröder et al., 2000; Schumann et al., 2017). In the UM, given its one-moment cloud scheme, the same PSD has to be specified for both contrail ice and natural cloud ice. The cross-sectional area C of the initial volume of contrails is assumed to be 100 m × 100 m for both CAM and UM simulations, similarly to Gettelman et al. (2021), the most recent CAM contrail study. We note that using the same cross-sectional area across different spatial resolutions of the two models is expected to have only a negligible effect on young-contrail properties. This is because the total contrail volume in a grid box depends not just on the cross-sectional area but also on the grid-box-aggregated distance flown, which ensures consistency across varying spatial resolutions.

2.3 Simulation setup

The models used in this study are configured in their respective standard setups, which are expected to be employed in future assessments of contrail cirrus simulations, similarly to evaluations conducted for other atmospheric agents. The spatial resolution of the UM follows its CMIP6 setup (Sellar et al., 2019), while CAM6 maintains the same horizontal resolution as its CMIP6 version (Danabasoglu et al., 2020), with an adjusted vertical resolution in the specified dynamics (nudging) configuration to align with MERRA-2 meteorology vertical layers. The nudging and time step settings used here reflect the default model configurations. Previous studies have quantified the impact of different configurations within a GCM, such as the impact of the microphysics scheme (Bock and Burkhardt, 2016) or the model resolution (Chen et al., 2012; Chen and Gettelman, 2013) on contrail cirrus ERF estimates. The model configurations of the UM and CAM used in this study are described in detail below.

The CAM simulations in this study were run using CAM6 at 1.25° longitude × 0.9° latitude horizontal resolution, 56 vertical levels (∼ 40 hPa/∼ 1000 m in the upper troposphere and lower stratosphere (UTLS)) from the surface to about 45 km, and a model time step of 30 min. The UM simulations use the Global Atmosphere 8.0 configuration (Walters et al., 2019) at UM version 12.0; a model time step of 20 min; and an N96L85 resolution, equating to a 1.9° longitude × 2.5° latitude horizontal resolution and 85 levels (∼ 18 hPa/∼ 500 m in the UTLS) in the vertical with a ∼ 85 km top.

We run 20 ensemble member simulations for each of the two models, with the imposed perturbations resulting in slightly different atmospheric evolution for each ensemble member to represent model uncertainty. For CAM, small random perturbations were imposed onto the initial temperature fields. In the UM, ensemble parameters from different physical parameterisations were perturbed with the random-parameter method following Bowler et al. (2008) and McCabe et al. (2016). All members in the CAM simulation are initialised on 1 January 2006 and run for 1 year. The UM was run for 1 year and 4 months, from 1 September 2005 to 31 December 2006, and the first 4 months was discarded and considered to be a spin-up period. We use Student's t test across the ensembles to test the significance of the results.

To allow both models to capture the relatively small contrail perturbations (compared to the model internal variability in clouds and radiation) and to enhance the signal-to-noise ratio, the u and v winds field were nudged to a prescribed climatology, thus maintaining the simulated model atmosphere in a “similar” weather state across all members and consequently reducing the model internal variability. Winds in the UM were nudged towards the ERA5 reanalysis (Hersbach et al., 2020) on a 6-hourly basis. CAM6 was run in a nudging configuration using the NASA MERRA-2 reanalysis (Gelaro et al., 2017) winds with a relaxation timescale of 24 h, which is close to the simulation setups in Gettelman et al. (2021), to produce a cloud climatology similar to that of the free-running CAM. We note that contrail spreading would be affected by the model wind fields, which in our UM and CAM simulations are nudged to ERA5 and MERRA-2 reanalysis, respectively. Therefore, differences in the wind fields between these two reanalyses will contribute to variations in the simulated contrail spreading across the two models.

3 Results

3.1 Ice supersaturation and contrail formation criteria in the UM and CAM6

The ice supersaturation generated by the host climate model is key for determining both the microphysical properties and the lifetime of the simulated contrail cirrus. Previous evaluation studies show good agreement between simulated UM and CAM ice supersaturation and observations (Chen et al., 2012; Irvine and Shine, 2015). The models' humidity has also been validated against observations and intercompared with other CMIP5 climate models (Jiang et al., 2012).

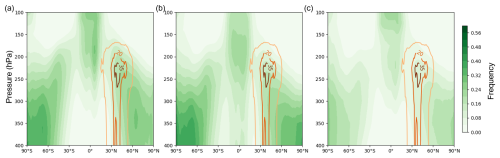
Figure 1 Annual zonal mean frequency of background ice supersaturation simulated by (a) the UM, (b) CAM, and (c) ERA5 for the full year of 2006. The ice supersaturation frequency is calculated on a 1 h basis. The coloured contour lines represent the annual zonal means of the flight distance (in m s⁻¹) in the AEDT air traffic inventory.

To evaluate the differences in the UM and CAM background meteorology, we analyse the frequency of background ice supersaturation simulated by the two models between the 100 and 400 hPa pressure levels in the control simulations (i.e. without aviation contrails) based on single deterministic runs (Fig. 1a and b). The ice supersaturation frequency pattern is similar in both models, with relatively high frequencies over middle and high latitudes below the tropopause and over the tropics in the UTLS. There is a hemispheric asymmetry in ice supersaturation frequency (larger in the Southern Hemisphere) shown in both the UM and the CAM simulations. The maxima in upper-tropospheric ice supersaturation in the UM expand higher up in the mid-latitudes compared to the CAM simulations, leading to the relatively high ice supersaturation frequency in the UM compared to CAM throughout much of the UTLS. In regions with intense air traffic (coloured contour lines in Fig. 1), the higher ice supersaturation frequency in the UM compared to CAM creates the potential for more persistent contrails in the UM. Both the UM and CAM capture the general pattern of ice supersaturation found in ERA5 (Fig. 1c). However, there are notable overestimations of ice supersaturation across much of the UTLS in both models compared to ERA5, which is known to have a dry bias in the UTLS (Kunz et al., 2014; Wolf et al., 2025). In high-latitude regions below the tropopause, the UM and CAM show ice supersaturation frequencies up to 50 % higher than those in ERA5. In the tropical tropopause layer, CAM simulates ice supersaturation frequencies closer to ERA5, while the UM still exhibits higher supersaturation frequencies.

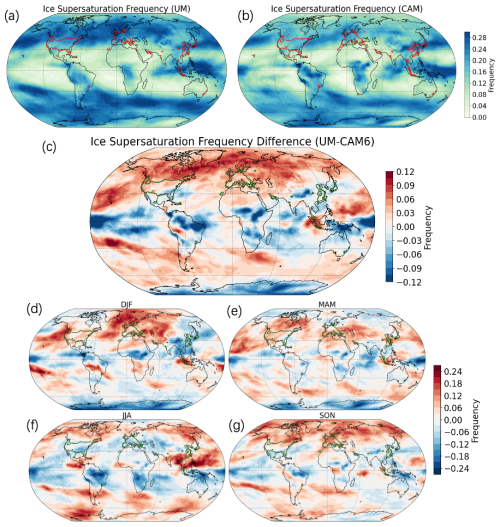
Figure 2 Maps of the annual mean background ice supersaturation frequency averaged between the 200 and 300 hPa pressure levels for 2006, generated by (a) the UM and (b) CAM. Panel (c) shows the difference in ice supersaturation frequency between the UM and CAM (UM minus CAM). Panels (d)–(g) show the seasonal mean of the ice supersaturation difference between the UM and CAM for 2006 in December–February (DJF), March–May (MAM), June–August (JJA), and September–November (SON), respectively. The green contour lines show where the mean flight distance in the AEDT air traffic inventory is over 50 m of aggregated flight distance per second.

Figure 2 shows the geographical distribution of averaged background ice supersaturation between the 200 and 300 hPa pressure levels (i.e. around the flight cruising levels) in the UM and CAM. The frequency of ice supersaturation in both the UM and CAM has a similar distribution pattern. There are however some important differences (illustrated in Fig. 2c), with the UM exhibiting higher and more widespread maxima than CAM, especially in regions of large air traffic density in the Northern Hemisphere, e.g. Europe and the continental USA, which again can potentially facilitate persistent contrail formation. Over East Asia, which is another air traffic hotspot, the ice supersaturation frequency between the UM and CAM6 is similar. The seasonal cycle of ice supersaturation frequency difference between the UM and CAM varies spatially as shown in Fig. 2d, e, f, and g. The UM in general has higher ice supersaturation frequency except for June–July–August over Europe and the continental USA. Over East Asia, the UM has lower ice supersaturation frequency apart from March–April–May. This seasonal cycle indicates a potential seasonal cycle of the differences in contrail cirrus estimates between the two models.

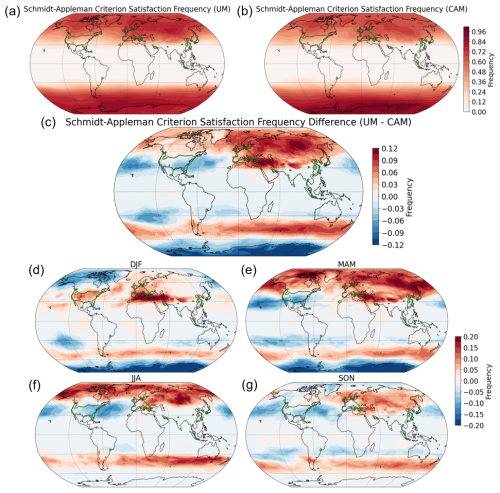
Figure 3 Maps of the annual mean Schmidt–Appleman criterion satisfaction frequency averaged between the 200 and 300 hPa pressure levels for 2006, simulated in (a) the UM and (b) CAM. Panel (c) shows the difference between the UM and CAM (UM minus CAM). Panels (d)–(g) show the seasonal mean of difference between the UM and CAM for 2006 in December–February (DJF), March–May (MAM), June–August (JJA), and September–November (SON), respectively. The green contour lines show where the mean flight distance in the AEDT air traffic inventory is larger than 50 m of aggregated flight distance per second.

The satisfaction frequencies of the Schmidt–Appleman criterion in the two models, averaged between the 200 and 300 hPa pressure levels, are illustrated in Fig. 3. The overall distribution patterns between the two models are similar (Fig. 3a and b), with both showing relatively high frequencies in middle and high latitudes. However, the UM has a higher frequency in some regions with intense air traffic (e.g. Europe, East Asia, North Atlantic), indicating a greater likelihood of contrail formation (Fig. 3c). Combined with its generally higher ice supersaturation frequency, this increases the probability of young-contrail formation and persistence in the UM. There is also seasonal variation in the differences in Schmidt–Appleman criterion satisfaction between the two models (Fig. 3d, e, f, and g). Over East Asia and most of Europe, the UM generally shows higher frequency during all seasons, except in western Europe during June–July–August and September–October–November. Over the continental USA, the UM generally exhibits higher frequencies in December–January–February but lower frequencies during the rest of the year.

3.2 Simulated young contrails

The fraction and ice mass mixing ratio of young contrails, i.e. the contrail in the first model time step of its life cycle, are diagnosed by the contrail parameterisation during each model time step. Subsequently, those contrails are added at the end of the time step as increments to the natural cloud fraction and ice mass mixing ratio. The geographical distributions of the annual mean contrail cover fraction and ice water path of young contrails in the UM and CAM are shown in Fig. 4. The contrail cover fraction geographical distribution is calculated based on the random overlap assumption over vertical layers. There are many similarities in the patterns of the fraction and ice water path of young contrails simulated by the two models, since both employ the same air traffic inventory. Contrails appear mostly over the Northern Hemisphere, with maxima over the continental USA and Europe and substantial quantities over the North Atlantic corridor and East Asia. However, the magnitude of both the fraction and ice water path of young contrails in the UM is substantially larger than in CAM, as summarised in Table 1. We estimate a global average young-contrail cover fraction of 0.00012 % in CAM and 0.00027 % in the UM. Over the high-air-traffic European region, defined here as 35–60° N latitude and 10° W–25° E longitude, the young-contrail cover fraction averages are 0.0015 % and 0.0048 % in CAM and the UM, respectively. There are also large differences in the simulated young-contrail ice water path. As shown in Eq. (4), the young-contrail fraction and ice water mass mixing ratio are proportional to the time step length. To ensure comparability of the young-contrail quantities, the CAM values were normalised to 30 min by a factor of $\mathrm{2}/\mathrm{3}$ to account for the different model time step lengths (i.e. 20 min in the UM and 30 min in CAM). The normalisation was applied after the random overlap in our study, and we found that the sequence of normalisation and random overlap only had a negligible effect on the young-contrail cover fraction. This normalisation may slightly underestimate CAM values, as it does not account for contrails lasting between 20 and 30 min. The larger fraction and ice water path values of young contrails simulated in the UM are due to the larger frequency of ice supersaturation and Schmidt–Appleman criterion satisfaction in the UM compared to CAM (Figs. 1, 2, and 3).

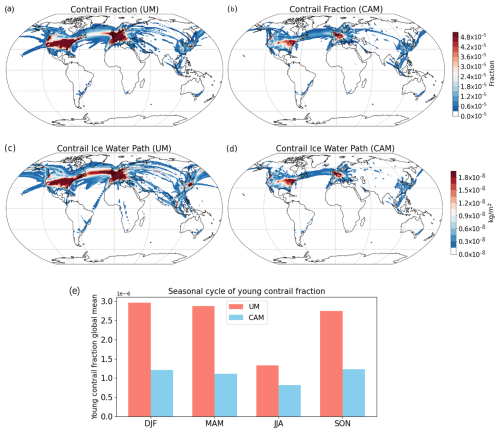
Figure 4 The annual mean young-contrail cover fraction (using the random overlap assumption) from (a) the UM and (b) CAM and the contrail ice water path from (c) the UM and (d) CAM using the AEDT air traffic inventory for 2006. Panel (e) shows the UM and CAM global seasonal mean young-contrail cover fraction. The results of CAM are normalised to 20 min by a factor of 0.67 to account for the different model time step lengths (i.e. 20 min in the UM and 30 min in CAM).

Table 1 Young-contrail diagnostics simulated by the UM and CAM using the AEDT air traffic inventory for 2006. The results of CAM are normalised to 20 min by a factor of 0.67 to account for the different model time step lengths (20 min in the UM, 30 min in CAM).

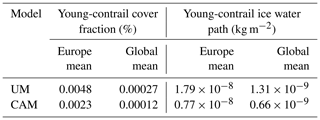
Young-contrail cover fractions of the UM and CAM have similar monthly variations, with minima and maxima in boreal summer and winter, respectively (Fig. 4e). This monthly variation is consistent with Chen et al. (2012) and other modelling and satellite observation-based studies (Bock and Burkhardt, 2016). The minima of the contrail cover fraction in boreal summer primarily result from the larger upper-tropospheric temperatures in the main regions of intense air traffic (i.e. Northern Hemisphere), which inhibit the formation of contrails. The young-contrail cover fractions of the two models are similar to one another during boreal summer, while during the other seasons the UM estimates are 2 to 3 times larger than those from CAM. The different magnitude of the seasonal cycle in the young-contrail cover fraction is consistent with the seasonal cycle of ice supersaturation frequency difference mentioned in Sect. 3.1. During the boreal summer, the global means of the young-contrail cover fraction simulated by the two models are more similar, largely due to the lower ice supersaturation in the UM over some of the regions with intense air traffic (e.g. Europe and the USA).

However, our simulated young-contrail cover fraction values are larger than the corresponding Chen et al. (2012) estimates, where the contrail parameterisation was implemented into the earlier CAM5 version of the model (compared to CAM6 version used in this study). Chen et al. (2012) reported a large dependence of the simulated young-contrail cover fraction on the number of vertical levels in the UTLS used in CAM, with differences of up to a factor of 10 between simulations using 1000 and 80 m vertical thickness in the UTLS. To account for this dependence, we compare the annual global mean young-contrail cover fraction of 0.00018 % (unnormalised, since the time steps for both CAM5 and CAM6 are identical) from our CAM6 simulations with 56 levels overall and ∼ 1000 m vertical level thickness in the UTLS with the corresponding value of 0.000061 % estimated in CAM5 with 30 vertical levels in total but a similar vertical interval in the UTLS (Chen et al., 2012). Our CAM6-simulated value is therefore ∼ 3 times larger than the CAM5 value reported in Chen et al. (2012), indicating the effect of the different model physics and simulated ice supersaturation frequencies in the two CAM versions. In addition, the finer UM vertical resolution in the UTLS also contributes to a larger young-contrail cover fraction (Chen et al., 2012).

We note that the young-contrail fraction presented here for both the UM and CAM only corresponds to persistent contrails created within one model time step and is therefore not directly comparable with the contrail fraction reported by other models. For instance, the ECHAM5-simulated contrail cirrus fraction of 0.74 % for contrail cirrus with an optical depth threshold of at least 0.05 also includes contrails older than one model time step (Bock and Burkhardt, 2016).

3.3 Simulated contrail impact on overall cloud fields

The UM and CAM employ distinct cloud and radiation schemes as mentioned in Sect. 2.1. To investigate the response of the two models' cloud schemes to the presence of contrail cirrus, we analyse the averaged differences between the 20 perturbed runs (with contrails) and the control ensemble runs (without contrails) for each model. We also assess the statistical significance of these differences using Student's t test, considering the change significant when the magnitude of local perturbations exceeds 2 standard deviations of the 20 ensemble members (i.e. 95 % confidence level).

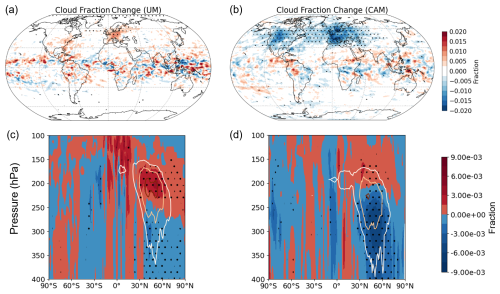
Figure 5 Annual mean total cloud fraction changes at 220 hPa from (a) the UM and (b) CAM and annual zonal mean of cloud fraction changes caused by contrails in (c) the UM and (d) CAM using the AEDT air traffic inventory for 2006. Dotted areas indicate statistically significant changes at the 95 % confidence level across the 20 ensemble member simulations. The contour lines represent the zonal mean young-contrail fraction above 0.00002 % (white), 0.0001 % (yellow), and 0.0003 % (brown).

Figure 5 shows the geographical distribution of the changes in the total cloud (i.e. natural + contrail) fraction due to the presence of contrails and their feedback on natural clouds. In the UM, the presence of contrails leads to a statistically significant increase in annual global mean total cloud fraction of about 0.004 %, with larger relative increases over European regions with large air traffic density, where the change amounts to up to 0.4 %. This overall cloud fraction response in the UM is consistent with other model studies (Bock and Burkhardt, 2016; Quaas et al., 2021). For example, the contrail cirrus simulations with the ECHAM model reported an overall relative increase in the total cloud fraction (natural cirrus + contrails) with a partly compensating effect due to the relative decrease in natural cirrus cover (Burkhardt and Kärcher, 2011; Bickel et al., 2020). In contrast, our CAM simulations indicate a strong relative reduction in the overall cloud fraction: −0.06 % globally and −0.7 % over Europe. From the vertical cross section in CAM, the relative decrease in the cloud fraction is mainly situated around and below the contrail formation areas (Fig. 5d). This relative reduction in cloud fraction in CAM has also been reported in Gettelman et al. (2021), where it was linked to the reduction in relative humidity caused by the local temperature increase from added contrail ice mass.

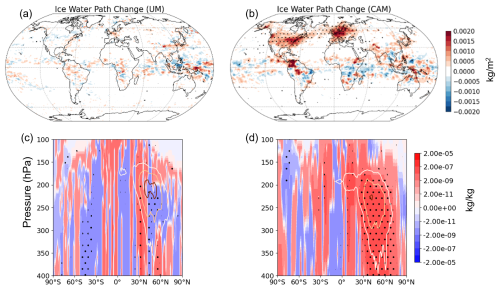
Figure 6 Annual mean contrail-driven cloud ice water path changes in kg m⁻² in (a) the UM and (b) CAM and annual zonal mean contrail-driven cloud ice water mixing ratio changes in kg kg⁻¹ in (c) the UM and (d) CAM using the AEDT air traffic inventory for 2006. Dotted areas indicate statistically significant changes at the 95 % confidence level across the 20 ensemble member simulations. The contour lines represent the zonal mean young-contrail fraction above 0.00002 % (white), 0.0001 % (yellow), and 0.0003 % (brown).

The simulated impact of contrails on the overall cloud ice water content in the UM is substantially smaller compared to the CAM simulations (Fig. 6). In terms of the cloud ice water path, the simulated response in the UM (Fig. 6a) only shows some slight increases due to the presence of contrails over Europe; over other regions, the changes are not significant due to small signal-to-noise ratios. There are decreases in the cloud ice mass mixing ratio around the contrail formation levels, likely driven by contrail longwave heating impacts (Fig. 6c), which are overcompensated for by increased cloud ice mass above and below the contrail formation levels. The small response in overall cloud ice content in the UM is very likely caused by the limitations of the one-moment cloud microphysics scheme used in the UM, where young contrails are assumed to have the same PSD as natural cirrus when added to the natural ice clouds. Also, all ice clouds, including contrails, are represented by a single ice category, with a PSD that spans the range from small crystals to large aggregates. Therefore, the contrail ice particles in the UM have much larger sizes and smaller number concentrations than those in CAM, which increases the sedimentation and sublimation rates of contrail ice particles. We note that sedimentation processes do not act as a sink term for the cloud fraction in the UM, as long as some ice mass remains in the grid box. Therefore, while contrail cirrus ice mass may sediment and sublimate relatively quickly, the contrail cirrus fraction is able to persist for longer (Fig. 5a and c). In the CAM simulations, the simulated response in the cloud ice water path consists in larger increases over more of the dense air traffic regions, e.g. over the European regions, North Atlantic, and USA (Fig. 6b). This results from increases in the cloud ice mass mixing ratio both at and below contrail formation levels, likely due to the falling of contrail ice (Fig. 6d).

3.4 Scaling the contrail cirrus radiative response in the UM

A key limitation of this contrail cirrus scheme in the UM comes from the inability of its one-moment cloud microphysics scheme to represent, for a given contrail ice mass, realistic contrail microphysical characteristics and associated radiative effects. To address this, we adopt a method to enhance the contrail radiative response by implementing a scaling factor in the model radiation scheme for the young-contrail ice mass initialised by the contrail parameterisation. The choice of this scaling factor is based on comparing the simulated UM contrail cirrus optical depth (the optical depth calculated by the changes in the total cloud optical depth including both contrails and natural clouds caused by contrails) with other existing contrail cirrus optical depth estimates. These include both our simulation results from CAM and the published results from ECHAM (Burkhardt and Kärcher, 2011; Bock and Burkhardt, 2016). To obtain the most suitable scaling factor for each optical depth reference value, we used a trial-and-error method based on several simulations spanning scaling factors between 1000 and 20 000. We used the European region (35–60° N latitude and 10° W–25° E longitude) as a benchmark due to its high air traffic density and therefore larger statistical significance. As a result, the scaling factors may not be representative of areas with lower air traffic density, where obtaining statistically significant results is more challenging. The range of scaling factors needed to match the range of European mean contrail cirrus optical depth reference values (i.e. 0.01–0.08) is shown in Table 2.

Table 2 Annual global mean contrail cirrus ERFs simulated in the UM when aligning its annual European mean contrail cirrus optical depth with that of three different reference models. The annual mean contrail cirrus optical depths over Europe and the scaling factors used for calibrating optical depth are also included in the table.

To further compare the differences between the UM and CAM contrail cirrus simulations, in the remainder of the paper, we adopt the scaling factor (i.e. 4900) corresponding to the European mean contrail cirrus optical depth simulated in CAM (i.e. 0.018) – we refer to this as the scaled-UM simulation. We note that this scaling is only applied in the model's radiation scheme (where the overall cloud ice mass used to determine the cloud radiative effect therefore includes the enhanced contrail ice mass) and does not affect the actual prognostic ice mass carried through the rest of the model (e.g. dynamics or microphysics).

3.5 Simulated contrail cirrus effective radiative forcing

We estimate the contrail cirrus ERF, including the radiative effects of the natural cloud feedback, by contrasting simulations with and without contrails. Figure 8 shows the simulated annual mean contrail cirrus ERF in our scaled-UM and CAM simulations using the AEDT air traffic inventory for 2006. The pattern of contrail cirrus ERF in the scaled-UM simulation is consistent with the cloud fraction (Fig. 5a) and cloud ice mass (Fig. 7a) change, with strong positive values over Europe and the USA. In CAM, the contrail cirrus ERF is consistent with the increase in cloud ice mass (Fig. 6b) but not with the decrease in the cloud fraction (Fig. 5b). There is a larger increase in the total cloud fraction in the cloud microphysics scheme in the scaled-UM run (not shown) compared to the unscaled-UM run (Fig. 5a). But the change in the cloud ice water path in the scaled-UM run (not shown) remains similar to that of the unscaled-UM run (Fig. 6a). The annual global mean contrail cirrus ERF is 25.7 mW m⁻² in the scaled-UM run and 52.5 mW m⁻² in the CAM simulations for 2006. The factor-of-2 difference between these values may partly be caused by the fact that our scaling approach only affected the contrails in the first time step of their life cycle. Besides this, it might also be due to the different radiative transfer schemes and different cloud microphysical process rates in the UM and CAM.

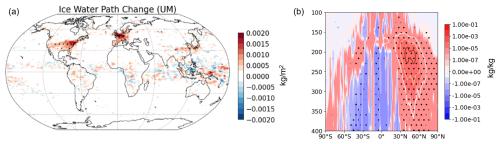
Figure 7 (a) Annual mean simulated contrail-driven changes in the cloud ice water path in kg m⁻² in the radiation scheme in the scaled-UM run (i.e. including the scaled-UM contrail mass) and (b) the annual zonal mean contrail-driven changes in the cloud ice mass mixing ratio in kg kg⁻¹ in the UM radiation scheme in the scaled-UM run using the AEDT air traffic inventory for 2006. These values are calculated as the difference between simulations with contrails and those without contrails. Dotted areas indicate statistically significant changes at 95 % confidence level. Note that the colour scale in (b) is significantly different compared to Fig. 6c and d. The contour lines represent the zonal mean young-contrail fraction above 0.00002 % (white), 0.0001 % (yellow), and 0.0003 % (brown).

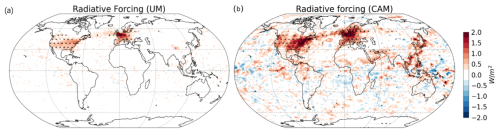
Figure 8 Annual mean contrail cirrus ERF from (a) the scaled-UM run and (b) CAM using the AEDT air traffic inventory for 2006. Dotted areas indicate statistically significant changes at the 95 % confidence level.

By considering the range of UM scaling factors in Table 2 covering existing model estimates for European contrail cirrus optical depth, we estimate a range of UM-simulated contrail cirrus ERFs between 11.1 and 91.0 mW m⁻² for 2006.

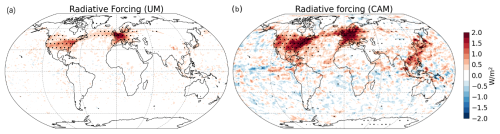
Figure 9 Annual mean contrail cirrus ERF from (a) the scaled-UM run and (b) CAM using the scaled AEDT air traffic inventory for 2018. Dotted areas indicate statistically significant changes at the 95 % confidence level.

We also estimate contrail cirrus ERF for the year 2018 with both the UM and CAM for comparison with the corresponding values reported in the latest IPCC AR (i.e. Lee et al., 2021). For our 2018 simulations, we apply the 2006–2018 air traffic volume scaling factor of 1.58, based on the growth in total aircraft distance travelled reported in Lee et al. (2021), to the AEDT inventory and re-run the scaled-UM and CAM simulations with the scaled AEDT inventory. Our 2018 contrail cirrus ERF estimates are 40.8 and 60.1 mW m⁻² from the scaled-UM and CAM simulations, respectively (Fig. 9), both within the Lee et al. (2021) 5 %–95 % likelihood range of 17–98 mW m⁻² for contrail cirrus ERF.

4 Summary and conclusions

In this study, we have implemented the Chen et al. (2012) contrail cirrus parameterisation from CAM in the UM. This allows us to simulate, for the first time, contrail cirrus formation and associated cloud and radiative feedbacks in the UM. Additionally, by analysing contrail cirrus simulations with the same contrail scheme in two different host climate models, we investigated the role of key model characteristics in contrail cirrus ERF uncertainty.

We found that differences in the simulated ice supersaturation frequency in the UM and CAM lead to a larger young-contrail ice water path and young-contrail fraction in the UM compared to CAM (by a factor of 2 to 3). This highlights the critical impact of the climate models' ability to accurately represent ice supersaturation in young-contrail simulations.

Our simulations indicate that the inclusion of contrails results in an increased total cloud fraction (natural clouds + contrails) in the UM but a decreased total cloud fraction in CAM due to differences in the representation of microphysical processes. Also, while there is an increase in the cloud ice water path in both models, this is much more pronounced in CAM. Our analysis indicates that this may be caused by the limitations of the one-moment cloud microphysics scheme and the single ice category in the UM. This results in unrealistically large sizes for contrail ice particles that affect the microphysical process rates and the life cycle of contrails in the UM. This highlights the importance of accounting for the difference in ice particle sizes between contrails and natural clouds and therefore the need for host climate models to use double-moment cloud microphysics schemes (Bock and Burkhardt, 2016).

To compensate for the incorrect representation of the contrail cirrus radiative effect in the UM, caused by the limitations of the one-moment cloud microphysics scheme, we scale up the contrail ice mass in the UM radiation scheme to match other existing European mean contrail cirrus optical depth estimates. Using this method, when matching different existing European mean contrail optical depth estimates, we obtain a range of 11.1–91.0 mW m⁻² contrail cirrus ERF for 2006 in the UM. When scaling to match the Europe mean contrail cirrus optical depth simulated in CAM, the UM estimates for the contrail cirrus ERF are 25.7 mW m⁻² for the year 2006 and 40.8 mW m⁻² for the year 2018, while the corresponding CAM estimates are 52.5 mW m⁻² for the year 2006 and 60.1 mW m⁻² for the year 2018. Both of the UM and CAM contrail cirrus ERF estimates for the year 2018 are within the uncertainty range reported in Lee et al. (2021).

In conclusion, we found substantial differences between the representation of contrail cirrus formation, persistence, and radiative effects in two different climate models. Our simulations indicate the following: (i) a factor of 2–3 uncertainty in the young-contrail cover fraction due to differences in the ice supersaturation frequency, (ii) contrasting (increase versus decrease) responses in the total cloud fraction due to contrails, (iii) a factor-of-2 uncertainty in contrail cirrus ERF due to the scaling approach used in the UM and the differences in the model microphysics and radiation schemes, and (iv) a factor-of-8 uncertainty in contrail cirrus ERF due to current uncertainty in simulated and/or observed regional contrail cirrus optical depths.

Another source of uncertainty arises from the differences in configurations (e.g. spatial and temporal resolutions, nudging) between the UM and CAM. In this study, both these widely used climate models are employed in their standard configurations, which are also likely to be used in future contrail studies.

Future work on contrail cirrus modelling in the UM should therefore focus on implementing not only (i) a contrail scheme coupled to the recently implemented double-moment cloud microphysics scheme (Field et al., 2023), but also (ii) a prognostic contrail scheme (e.g. Burkhardt and Kärcher, 2009) to allow for the detailed representation of the young-contrail evolution to contrail cirrus. Another key areas for future work consist in additional climate models to better assess the uncertainties in model physics and observation studies to better constrain the contrail cirrus radiative effects.