Uncertainties in cloud-radiative heating within an idealized extratropical cyclone

Cloud-radiative heating (CRH) within the atmosphere affects the dynamics and predictability of extratropical cyclones. However, CRH is uncertain in numerical weather prediction and climate models, and this could affect model predictions of extratropical cyclones. In this paper, we present a systematic quantification of CRH uncertainties. To this end, we study an idealized extratropical cyclone simulated at a convection-permitting resolution of 2.5 km and combine large-eddy-model simulations at a 300 m resolution with offline radiative transfer calculations. We quantify four factors contributing to the CRH uncertainty in different regions of the cyclone: 3D cloud-radiative effects, parameterization of ice optical properties, cloud horizontal heterogeneity, and cloud vertical overlap. The last two factors can be considered essentially resolved at 300 m but need to be parameterized at a 2.5 km resolution. Our results indicate that parameterization of ice optical properties and cloud horizontal heterogeneity are the two factors contributing most to the mean uncertainty in CRH at larger spatial scales and can be more relevant for the large-scale dynamics of the cyclone. On the other hand, 3D cloud-radiative effects are much smaller on average, especially for stratiform clouds within the warm conveyor belt of the cyclone. Our analysis in particular highlights the potential to improve the simulation of CRH by better representing ice optical properties. Future work should, in particular, address how uncertainty in ice optical properties affects the dynamics and predictability of extratropical cyclones.

1 Introduction

Our ability to predict extratropical cyclones is crucial for midlatitude weather, as they are often associated with strong winds, heavy rain, and snow. Cloud diabatic processes, such as latent heat release due to phase changes in water, play an important role in shaping the dynamics of extratropical cyclones (Ahmadi-Givi et al., 2004; Booth et al., 2013; Binder et al., 2016). However, recent studies have shown that the impact of cloud-radiative heating and cooling (hereafter CRH) on the dynamics of extratropical cyclones can also be substantial (Schäfer and Voigt, 2018; Keshtgar et al., 2023; Voigt et al., 2023). Our study is motivated by the CRH impact.

Within the atmosphere, CRH results from the interaction of clouds with radiation in different parts of the electromagnetic spectrum. In the shortwave spectrum, clouds absorb the incoming shortwave radiation, which warms clouds and contributes to their stabilization. In the longwave spectrum, clouds absorb outgoing longwave radiation at their bases and re-emit it at colder temperatures at their tops, leading to substantial cooling. This pattern of cloud top cooling and modest warming from below promotes convective instability within the cloud (Webster and Stephens, 1980). By doing so, CRH can alter cloud microphysical heating and precipitation (Klinger et al., 2017) and the intensity and predictability of an idealized extratropical cyclone (Keshtgar et al., 2023). Voigt et al. (2023) showed that the impact of CRH on extratropical cyclones differs between low-level and high-level clouds, implying that cyclones may respond differently to CRH depending on the vertical distribution of clouds. On the longer timescales of climate, modeling studies showed that CRH impacts the planetary-scale circulation of the atmosphere and its response to surface warming (Li et al., 2015; Voigt et al., 2020).

Small errors in the parameterization of sub-grid-scale physical processes can quickly grow to the synoptic scale, leading to forecast errors of a significant magnitude (e.g., Baumgart et al., 2019). The interaction between radiation and clouds is known to be uncertain due to many factors, such as simplified radiation schemes or poor representations of clouds in models. Keshtgar et al. (2023) showed that modulation of latent heating by CRH within the ascending region of the cyclone changes the vertical motion and the divergent flow near the tropopause. After the divergent flow has changed, changes in potential vorticity are amplified by the rotational flow near the tropopause during the highly nonlinear stage of cyclone evolution. Keshtgar et al. (2023) further demonstrated that CRH continuously changes the latent heating during the growth phase of the cyclone. This result indicates that CRH uncertainties might affect the magnitude of latent heating and be relevant for error growth near the tropopause.

The correct simulation of CRH is challenging. Several previous studies have addressed the question of how the simulation of CRH depends on model assumptions, the representation of clouds in models, and the parameterization of radiative processes. Compared to models with coarse horizontal resolutions of 10–100 km and with parameterized convection, clouds can be better simulated in kilometer-scale models and even better simulated in large-eddy models (Griewank et al., 2020; Stevens et al., 2020). In this paper, we make use of these modeling advances to present the first systematic assessment of CRH uncertainty within an extratropical cyclone by simulating the same idealized cyclone as in Keshtgar et al. (2023) at a convection-permitting resolution of 2.5 km. We further run large-eddy-model simulations at a horizontal resolution of 300 m for different regions of the cyclone and use their output for offline radiative transfer calculations. We assume that we have perfect knowledge of the clouds from the large-eddy-model simulations, and this leads us to prioritize the following four factors as potential sources of uncertainty in CRH in our study.

• 3D cloud-radiative effects. The 3D cloud-radiative effects arise from horizontal photon transport that is not taken into account in 1D radiation schemes, as is currently operational in weather and climate models. The main 3D cloud-radiative effects are shortwave cloud-side illumination (Jakub and Mayer, 2015, 2016), shortwave cloud-side radiation leakage (Hogan and Shonk, 2013), and longwave cloud-side absorption and emission (Klinger et al., 2017). At high solar zenith angles, shortwave cloud-side illumination increases the shortwave absorption at the cloud sides facing the sun. At low solar zenith angles, however, photons can escape through cloud sides and lead to a reduction in shortwave cloud absorption. In the longwave, the horizontal transport of photons through cloud sides increases cloud-radiative cooling. Thus, the largest differences between 3D and 1D radiative transfer calculations are expected to occur between cloudy and clear model grid boxes, where the gradient of cloud optical properties is large. Strong horizontal variability in in-cloud and sub-grid cloud optical properties can also lead to horizontal radiative transfer that is neglected in 1D radiative transfer schemes. Since we can assume that the clouds from the large-eddy-model simulations are perfectly known and no further sub-grid cloud variability exists, 3D cloud-radiative effects here are only attributed to the horizontal gradient of radiative fluxes between model columns and not to those within model grid boxes. For model grids with coarser horizontal resolutions, the horizontal radiative exchange caused by the horizontal sub-grid variability in cloud optical properties needs to be parameterized as part of the 3D cloud-radiative effects.

• Ice optical parameterization. The representation of ice optical properties in models is challenging due to the complexity of ice crystals, especially due to assumptions regarding their shape and surface roughness. The lack of a consolidated understanding of the ice crystal shapes and how they should be represented in models creates an important source of uncertainty for simulating CRH (e.g., Zhao et al., 2018; Yi, 2022). Several parameterizations for the ice optical properties have been developed based on different assumptions about ice crystal shapes or habits, size distributions, and surface roughness (Yang et al., 2013; Baran et al., 2014; Baum et al., 2014). It is therefore important to examine how the assumed ice optical properties affect CRH.

• Cloud horizontal heterogeneity and vertical overlap. Clouds are not homogeneous over their horizontal and vertical extents, and this spatial variability significantly affects their interactions with radiation. Cloud horizontal heterogeneity refers to the horizontal variation in cloud optical properties within a grid box. The vertical overlap determines how cloud layers are stacked on top of each other. The ability of models to account for cloud horizontal heterogeneity and vertical overlap depends primarily on their horizontal resolutions. In large-eddy-model simulations, we can assume that there are no further sub-grid cloud variabilities, and clouds are entirely characterized by the grid-box values. Thus, we quantify these sources of uncertainty at the convective-permitting resolution of 2.5 km for the numerical weather prediction model. Neglecting cloud horizontal heterogeneity increases longwave emissivity and shortwave absorption of clouds, an effect known as the plane-parallel problem of radiative transfer calculations (e.g., Črnivec and Mayer, 2019). In current models with resolutions on the order of 1–10 km, parameterizations are used to represent both cloud horizontal heterogeneity within grid boxes and cloud vertical overlap between adjacent grid boxes. As a result, assumptions in the parameterizations of these two sub-grid effects can lead to errors in the simulation of CRH (e.g., Wang et al., 2021).

We organize the paper as follows. The model simulation setup and radiative transfer calculations are described in Sect. 2. In Sect. 3 we quantify the CRH uncertainty due to the four factors discussed above, and we compare their importance in Sect. 4. The paper closes with a discussion and conclusion in Sect. 5.

2 Methods

This section describes the model setup for the idealized baroclinic life cycle simulation, the large-eddy-model simulations, and the offline radiative transfer calculations that we use in combination to investigate the uncertainty in CRH within an extratropical cyclone.

2.1 Baroclinic life cycle simulation

We use the ICOsahedral Nonhydrostatic atmosphere model (ICON version 2.6.2.2; Zängl et al., 2015) to simulate a baroclinic life cycle. The simulation provides us with an idealized extratropical cyclone for which we can test the uncertainty in CRH. We use the same model setup developed and described by Keshtgar et al. (2023) and only briefly describe the model setup here. The planar channel grid extends 4000 and 9000 km in the zonal and meridional directions, respectively. The horizontal resolution is 2.5 km. Periodic boundary conditions are applied in the zonal direction, and the Coriolis parameter is set to a uniform value valid at 45° N. ICON applies a terrain-following hybrid vertical coordinate, and we use 75 model levels in the vertical direction. The layer thickness increases from 20 m near the surface to 400 m at an altitude of 10 km. Above 10 km, the layer thickness increases from 400 to 1200 m at 30 km. The initial and lateral boundary conditions follow the life cycle type 1 of Polvani and Esler (2007). The model surface is configured as an ice-free ocean with a prescribed sea surface temperature that is 0.5 K lower than the initial temperature of the lowest model level. To trigger the development of the cyclone, we add a temperature perturbation with a wavelength equal to the domain length and an amplitude of 1 K at all levels. We run the ICON model with the numerical weather prediction (NWP) physics package, including the shallow-convection scheme of Bechtold et al. (2008), the two-moment microphysics of Seifert and Beheng (2006), and the turbulence scheme of Raschendorfer (2001). Due to the high horizontal resolution of the model, deep convection is treated explicitly.

We use the modeling technique developed by Keshtgar et al. (2023) to simulate the cyclone with only the contribution of CRH; clear-sky radiative heating is not used to step the temperature forward in time. The CRH in the model is given by

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\partial T}{\partial t}}{|}_{\text{radiation}}^{\text{cloud}}& ={\displaystyle \frac{\partial T}{\partial t}}{|}_{\text{radiation}}^{\text{all-sky}}-{\displaystyle \frac{\partial T}{\partial t}}{|}_{\text{radiation}}^{\text{clear-sky}}\\ & ={\displaystyle \frac{\mathrm{1}}{\mathit{\rho }{c}_v}}\cdot {\displaystyle \frac{\partial }{\partial z}}(F^{\text{all-sky}}-F^{\text{clear-sky}}),\end{array}\end{array}$$

where ρ is the air density and F is the radiative flux in all-sky and clear-sky conditions defined as a positive downward flux. Since ICON is based on height levels, the conversion of radiative fluxes to heating rate requires the heat capacity of air at constant volume, c_v. As described in Keshtgar et al. (2023), the technique eliminates the impact of strong clear-sky radiative cooling early in the simulation.

Different from Keshtgar et al. (2023), we use ecRad (Hogan and Bozzo, 2018), the new operational radiation scheme in ICON (Rieger et al., 2019), instead of the Rapid Radiative Transfer Model (Mlawer et al., 1997). The advantage of ecRad is that we can configure the offline radiative transfer setup in a manner that is very close to the radiative transfer setup used in ICON (Sect. 2.3). From the various radiation solvers available in ecRad, we use the homogeneous solver. The solver homogenizes the cloud properties over the entire grid box; i.e., it ignores the cloud fraction and does not require any assumption about cloud vertical overlap. Thus, for the purpose of radiative transfer calculation, clouds are treated as grid-box clouds. This treatment is the same as in the large-eddy-model simulations described later. For the cloud optical parameterization, we use the scheme from the Suite Of Community RAdiative Transfer codes (SOCRATES) based on Edwards and Slingo (1996) for liquid water droplets. For ice crystals, we use the scheme of Fu (Fu, 1996; Fu et al., 1998).

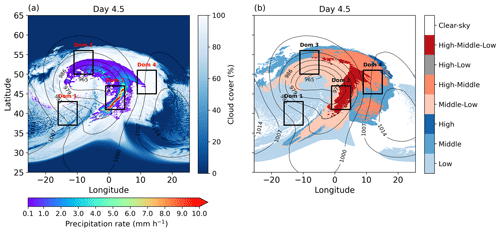
Overall, this model configuration results in a typical wintertime extratropical cyclone (Fig. 1a). Note that for the latitude–longitude plots, we use the geographic coordinates assigned during the generation of the planar channel grid, but the model simulation is based on the Cartesian coordinate of the grid. The baroclinic simulation provides the initial and lateral boundary conditions for the large-eddy-model (LEM) simulations described in the following section.

Figure 1 (a) Surface pressure (black contours; hPa), cloud cover, and precipitation at day 4.5 in the baroclinic life cycle simulation with ICON-NWP. Panel (b) shows cloud classes. The rectangles in both panels indicate the locations of the domains for the LEM simulations.

2.2 Large-eddy-model simulations

We target four different regions of the cyclone using the large-eddy-model simulations, shown as black rectangles in Fig. 1. To characterize the 3D structure of clouds, panel (b) of Fig. 1 shows cloud classes. We derive the cloud classes from the cloud vertical extent (Sullivan et al., 2023) using a 50 % threshold for low-, mid-, and high-level cloud cover that is diagnosed within ICON during the model simulation. For example, if cloud cover exceeds the 50 % threshold at low, middle, and high altitudes, the cloud class is “high-middle-low”.

Domain 1 targets low-level shallow cumulus and stratocumulus clouds southwest of the cyclone center within the cold sector. These clouds are formed by the passage of cold, dry air over the warm ocean behind the cold front. Domain 2 targets the extensive vertical clouds within the warm conveyor belt (WCB) of the cyclone, where strong latent heating and precipitation occur. Domain 3 captures mid- and low-level clouds in the cyclonic branch of the WCB outflow, and domain 4 captures mostly mid- and high-level clouds in the anticyclonic branch of the WCB outflow. We will refer to domains 1, 2, 3, and 4 as shallow cumulus, WCB ascent, WCB cyclonic outflow, and WBC anticyclonic outflow, respectively.

For the LEM simulations, we use the ICON model in a limited area setup. The LEM simulations use a planar grid with perfectly uniform triangular grid-cell areas. Unlike the planar channel grid used in the NWP simulation, the planar grid does not apply zonal periodic and fixed meridional boundary conditions. Instead, hourly lateral boundary conditions are provided by the baroclinic life cycle simulation. The planar grid extends 471 and 667 km in the zonal and meridional directions, respectively. This is approximately equivalent to a 6°×6° domain at 45° N. The horizontal resolution is 300 m. We use 150 model levels with layer thicknesses increasing from 20 m near the surface to 570 m at 30 km.

As in the NWP simulation, we run the LEM simulations with the two-moment microphysics scheme, the homogeneous radiation solver of ecRad, the same-cloud optical parameterization, and only the CRH contribution from the radiation scheme. In contrast to the NWP simulation, we use the 3D Smagorinsky diffusion model (Smagorinsky, 1963) for the turbulence scheme and switch off the shallow convection scheme. We configure the cloud cover scheme to treat clouds as grid-scale quantities; i.e., grid boxes are either fully cloudy or clear.

We run LEM simulations for 12 h starting on day 4.25 of the baroclinic life cycle simulation when the cyclone is in its main growth phase. We exclude the first 3 h to remove spin-up effects. Keshtgar et al. (2023) showed that between days 4 and 5, the modulation of latent heating by the CRH is strong enough to affect the dynamics of the cyclone.

The offline radiative transfer calculations described in Sect. 2.3 require as input the 3D fields of cloud ice and liquid water content and effective particle radii simulated by the large-eddy model. We briefly characterize the clouds from the LEM simulations in Fig. 2, which shows domain and time averages of cloud ice contents, liquid water contents, and cloud fractions for the four LEM domains. We calculate the time average over nine snapshots that are each separated by a 30 min time interval between 12:30 and 16:30 domain local time (DLT). We use the same snapshots for the offline radiative transfer calculation. During this time interval, the solar zenith angles change from low to high values in all regions, which is an important factor for the shortwave 3D cloud-radiative effects (Sect. 3.2).

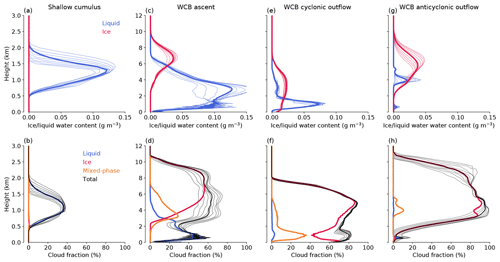
Figure 2 Profiles of domain-averaged cloud hydrometeor contents and total cloud fraction, decomposed into the contributions from liquid, ice, and mixed-phase clouds for all four LEM domains. Thin lines show profiles for nine snapshots between 12:30 and 16:30 DLT. The thick lines show time-averaged profiles. The threshold used to determine cloudy grid boxes for both ice and liquid water contents is 10⁻⁸ kg kg⁻¹ (Costa-Surós et al., 2020). Note the different y axes for panels (a) and (b).

In the shallow cumulus region, low-level liquid clouds prevail in the boundary layer between 0 and 2 km, with cloud fraction peaking at 40 % at an altitude of around 1 km (Fig. 2a and b). In the WCB ascent region, extensive vertical clouds contain both ice and liquid water. The liquid water content in the lower and middle levels is much higher and more variable in time than the ice water content in the upper levels (Fig. 2c). The decomposition of cloud fraction shows that liquid clouds are concentrated in the lower levels between 0 and 4 km, where their cloud fraction reaches a maximum of 60 % at around 1 km. Mixed-phase clouds are located at intermediate levels between 2 and 7 km. Above the boundary layer, the fraction of ice clouds increases rapidly, reaching a maximum of nearly 60 % at about 8 km (Fig. 2d).

Clouds in the WCB cyclonic outflow region also contain both ice and liquid water but are located at lower altitudes compared to the WCB ascent region (Fig. 2e). The total cloud fraction is dominated by ice clouds and reaches nearly 90 % at around 6 km. Mixed-phase clouds exist only in the boundary layer (Fig. 2f). In the WCB anticyclonic outflow, mid- and high-level clouds contain both ice and liquid water, with ice water content dominating over liquid water content (Fig. 2g). The total cloud fraction is dominated by ice clouds (Fig. 2h).

The WCB ascent and outflow regions are much cloudier than the shallow cumulus region. In the WCB outflow regions, stratiform ice clouds cover almost the entire domain.

2.3 Offline radiative transfer calculations

For the offline radiative transfer calculations, we use the libRadtran software (Mayer and Kylling, 2005; Emde et al., 2016), which includes several radiation solvers and different cloud optical parameterizations. In order to achieve the best possible match between the offline calculations and the CRH calculated with ICON, we configure the radiative transfer setup of libRadtran as similarly as possible to ICON.

For gas absorption, we use the parameterization of Fu (Fu and Liou, 1992, 1993), which employs the correlated k-distribution method with 6 and 12 spectral bands in the solar and thermal spectra, respectively. This parameterization is optimized for use in climate models. The optical properties of cloud droplets are prescribed according to the parameterization of Hu and Stamnes (1993), which assumes spherical droplets. The optical properties of ice crystals are prescribed according to the parameterization of Fu (Fu, 1996; Fu et al., 1998), which is the same scheme used in the ICON simulations. The scheme of Fu uses an approximate phase function and assumes a pristine hexagonal column habit for the ice crystals. For the radiative transfer solver, we use the classical δ-Eddington two-stream solver (Zdunkowski et al., 2007), which is suitable for horizontally homogeneous clouds. This solver is similar to the ecRad homogeneous solver used in the ICON simulations.

In libRadtran, inputs are required to have normal Cartesian rectangular coordinates. Therefore, we remap the LEM simulation output from the unstructured triangular grid to a regular Cartesian grid with the same resolution using nearest-neighbor interpolation. For the clear-sky background, we use pressure, temperature, density, specific humidity, and trace gas concentration from the LEM simulations. We set other inputs such as surface type, albedo, and emissivity to the same values as those used in the ICON simulations. We use the solar zenith angles used in the LEM simulations for the offline solar radiative transfer calculations.

The offline radiative transfer calculations are very time-consuming, especially the 3D Monte Carlo radiative transfer calculation (Mayer, 2009). Ideally, one would run the calculations over the entire LEM domain using the 3D cloud and clear-sky fields. However, this is not feasible because libRadtran cannot be run in parallel, and the wall-clock time of the computing nodes of the German Climate Computing Center (DKRZ) Levante supercomputer that we use for our study is limited to 8 h. To overcome the computational challenge, we divide the LEM domains into 36 1°×1° sub-domains for which we run the radiative transfer calculations individually. For each sub-domain, we use a 1D clear-sky background profile that we derive by horizontally averaging the clear-sky fields. After the radiative transfer calculations for all sub-domains are finished, we merge the results to obtain the radiative heating rate over the entire LEM domain. While this means that we neglect horizontal variability in the clear-sky background within the sub-domains, we show in Sect. 3.1 that this has a negligible impact, and we are able to achieve very good agreement between the CRH calculated offline with libRadtran in the reference setup using the 1D radiation calculation and online in ICON-LEM.

Partitioning of the LEM domains into sub-domains allows us to perform expensive 3D Monte Carlo radiative transfer calculations but can introduce errors in the radiative transfer calculations due to the discontinuity of the horizontal photon propagation at the lateral boundaries of the sub-domains. As an example, consider a shortwave radiative transfer calculation for a cumulus cloud near the northern boundary of a sub-domain. The shadow of this cloud should be present at the southern boundary of the sub-domain to the north of it, yet the periodic boundary conditions applied in the 3D solver mean that the shadow is placed at the southern boundary of the cloud's own sub-domain. The gravity of such an error depends on the solar zenith angle, cloud top height, and cloud cover. We minimize this issue by making the sub-domains overlap by approximately 12 km in all directions. The overlap is sufficient for shallow cumulus clouds with a maximum height of 2 km. The overlap is too small for clouds at higher altitudes in the WCB, but since WCB clouds are mostly stratiform, the resulting errors tend to be small and do not affect the generality of our results.

To investigate the uncertainty in CRH, we perform several radiative transfer calculations that are listed in Table 1. For 3D cloud-radiative effects, we use the “Monte Carlo code for physically correct tracing of photons in cloudy atmospheres” (MYSTIC; Mayer, 2009). MYSTIC can also be run in independent column approximation mode (MYSTIC-ICA), which neglects horizontal photon transport between model columns and is equivalent to a 1D radiation scheme. We use the standard forward photon tracing method. The azimuth angle is set to a constant value of 180°, which directs the solar radiation from south to north. To reduce the Monte Carlo noise, we run MYSTIC and MYSTIC-ICA with 7.2×10⁶ photons for each sub-domain in the LEM domains at each time step and repeat the calculations 10 times, resulting in a total of 7.2×10⁷ photons traced per sub-domain (nearly 5000 photons per LEM column). We then average these 10 calculations to derive the radiative heating in each LEM domain. Overall, the total computational time required to perform the entire set of 3D radiative transfer calculations amounts to about 1500 h on a single node of the DKRZ Levante supercomputer.

Table 1 List of radiative transfer calculations to quantify the uncertainty in CRH. The first column shows the purpose of the calculations, the second column the radiation solvers, and the third column the ice optical parameterization. The last column lists the sections in which the calculations are discussed.

To estimate the Monte Carlo noise of the MYSTIC solver in our setup, we split the 10 MYSTIC calculations for the shallow cumulus domain at a single time step into two sets of 5 calculations and average the heating rates over these two sets of 5 calculations. We then calculate the relative standard deviation of the radiative heating between these two sets at each grid box. The relative standard deviation represents the variability in the radiative heating relative to the mean values calculated from the two sets of MYSTIC calculations. The median relative standard deviations in the shortwave, longwave, and net are less than 10 % for almost all grid boxes (not shown). This estimate is an upper bound, as the true Monte Carlo noise in our calculations with 7.2×10⁷ photons can be expected to be smaller. The low Monte Carlo noise of our radiation calculation allows us to calculate the CRH uncertainty due to 3D cloud-radiative effects locally at the scale of the horizontal grid resolution of the LEM domains (Sect. 4).

To assess the impact of the ice optical parameterization, we use the more complex scheme of Baum_v36 (Yang et al., 2013; Baum et al., 2014) in addition to the scheme of Fu. The scheme of Baum includes the full phase function and three different ice habits: the general habit mixture, the solid column habit, and the rough-aggregated habit. Ice crystal surfaces are treated as severely roughened in the Baum scheme. Zhao et al. (2018) compared the radiative fluxes calculated with the schemes of Fu and Baum and showed that in the longwave spectrum, the mass absorption coefficient is smaller in the Baum scheme than in the Fu scheme, resulting in weaker longwave radiative cooling at the cloud top and weaker warming below (Fig. 1 of Zhao et al., 2018). In the shortwave spectrum, the backward scattering of radiation by ice crystals is higher in the Baum scheme due to the reduced parameterized asymmetry factor and the forward peak. This reduces the radiative flux gradient between cloudy and clear-sky layers, resulting in a weaker CRH with the ice scheme of Baum.

When studying the impact of cloud horizontal heterogeneity on CRH, it would be misleading to directly compare the CRH between the NWP and LEM setups since the two setups simulate different clouds. Therefore, we instead create homogeneous clouds at the 2.5 km NWP resolution by coarse-graining the LEM clouds. The method is illustrated in Fig. 3. We derive two types of homogeneous NWP clouds. For the first type, we average the cloud fields over all LEM grid boxes that fall within the corresponding NWP grid box with a resolution of 2.5 km. We call this type “homogeneous grid-box clouds”. This type assumes that clouds are resolved at the NWP resolution so that grid boxes are either entirely cloudy or clear and that no vertical overlap assumption is needed. For the second type, we average the cloud fields only over those LEM boxes that are cloudy, and we use the number of clear-sky boxes to determine the cloud fraction. We refer to this type as “homogeneous clouds with fractional cloud cover”. This type requires an overlap assumption, for which we use the δ-Eddington two-stream solver that applies maximum-random overlap (Črnivec and Mayer, 2019).

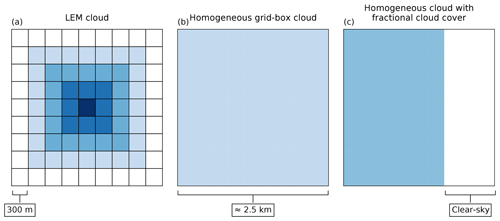
Figure 3 Illustration of the method used to derive homogeneous NWP clouds from LEM clouds. The plot shows a layer of grid boxes. (a) Clouds in the LEM simulation. (b) A homogeneous grid-box cloud at a resolution of 2.5 km. (c) A homogeneous cloud with fractional cloud cover at a resolution of 2.5 km.

3 Results

In this section, we assess CRH in the four regions of the cyclone. We derive CRH from all-sky and clear-sky radiative heating in the shortwave and longwave spectra for each of the radiative transfer settings listed in Table 1. To quantify the impact of the four factors described in Sects. 1 and 2, we compare the time and domain averages of the CRH from the different radiative transfer calculations.

3.1 Average profiles of CRH

Figure 4 shows domain and time averages of longwave, shortwave, and net CRH in the four regions of the cyclone for the ICON and the reference offline radiative transfer calculations. Despite the differences in the radiative transfer setup between ICON and libRadtran, the CRH profiles agree very well (cf. dashed and solid lines in Fig. 4). In all four regions, longwave radiation leads to cooling at the cloud tops and weak warming at the cloud bases (Fig. 4; blue), resulting in radiative destabilization of the cloud. In contrast, shortwave radiation warms the cloud tops and slightly cools the lower parts of the clouds, resulting in radiative stabilization of the cloud (Fig. 4; red). The longwave CRH is about twice as large as the shortwave CRH. Thus, the net CRH profiles are dominated by the stronger longwave CRH (Fig. 4; black).

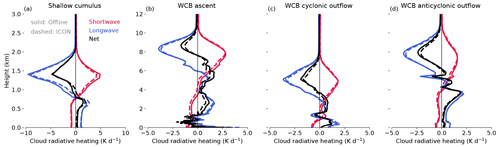
Figure 4 Domain and time averages of shortwave, longwave, and net CRH. Profiles are shown for (a) shallow cumulus, (b) WCB ascent, (c) WCB cyclonic outflow, and (d) WCB anticyclonic outflow regions. The ICON CRH is shown with dashed lines, and the CRH derived from the offline reference 1D radiative transfer calculation is shown with solid lines. Note the different x and y axes in panels (a) and (b–d).

The CRH in the shallow cumulus region is almost twice as strong as in the WCB regions (Fig. 4a). Grise et al. (2019) and Voigt et al. (2023) showed that the strong cloud-radiative cooling of the boundary layer has a weakening effect on the intensity of extratropical cyclones. The CRH in WCB regions is strongly influenced by the radiative heating of the ice clouds (Fig. 4b–d). Although the CRH in the WCB regions is weaker than the CRH in the shallow cumulus region, previous work showed it to be important for the near-tropopause dynamics of the cyclone (Li et al., 2015; Keshtgar et al., 2023; Voigt et al., 2023). Thus, it is important to quantify CRH uncertainties in all four regions of the extratropical cyclone.

3.2 3D cloud-radiative effects

We quantify 3D cloud-radiative effects as the difference in CRH between that calculated with the MYSTIC solver (3D; Sect. 2.3) and that with the MYSTIC solver run in the independent column approximation mode (1D). The latter is a 1D radiation scheme and neglects horizontal photon transport between model columns. To visualize the 3D cloud-radiative effects, Fig. 5 shows cross-sections of 3D and 1D all-sky radiative heating and their differences in shallow cumulus clouds southwest of the cyclone center at 16:30 DLT. At this location and time, the solar zenith angle is approximately 65°.

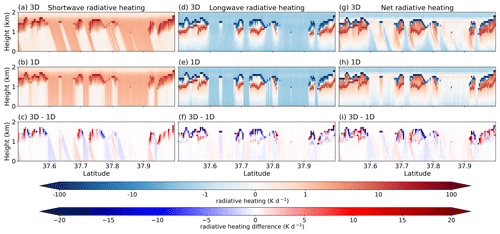
Figure 5 Cross-sections of shortwave, longwave, and net all-sky radiative heating visualized using a logarithmic color scale for shallow cumulus clouds southwest of the cyclone center. The upper row shows 3D calculations, the middle row shows 1D calculations, and the lower row shows the differences between the 3D and 1D calculations. The cross-sections are at 16:30 DLT and 11.5° W and between 37.5 and 38° N. The solar zenith angle is 65°. Note that the impression of a lower solar zenith angle in the figure is due to the aspect ratio of the figures.

In the shortwave spectrum, neglecting horizontal photon transport leads to incorrect positions of illuminated and shadowed areas in the atmosphere and on the surface (Fig. 5a–c). Črnivec and Mayer (2019) showed that this can have a substantial impact on surface radiative fluxes and hence the surface energy balance. However, our focus is on the 3D radiative effects of clouds within the atmosphere. In Fig. 5a, the southern sides of the clouds (see the shallow cumulus domain in Fig. 1) facing the sun receive more radiative energy in the 3D calculation than in the 1D calculation (red colors around 1.5 km in altitude in Fig. 5c). In some cases, the northern sides of the clouds are shadowed and receive less energy (blue colors around 1.5 km in altitude in Fig. 5c). The shortwave cloud-side leakage is small in this example due to the low position of the sun.

In the longwave spectrum, cloud “shadows”, visible as white areas below clouds (panels d and e of Fig. 5), are weaker in the 3D calculation than in the 1D calculation due to the horizontal photon transport between model columns. However, the largest differences between the 3D and 1D calculations occur at the cloud–clear-sky boundaries, where horizontal emission of longwave radiation from the cloud tops and cloud sides leads to stronger radiative cooling in the 3D calculation (blue colors around 1.5 km in height in Fig. 5f).

In the net, most features of cloud-radiative heating and cooling within the atmosphere are present in both 3D and 1D calculations (Fig. 5g and h). However, due to shortwave cloud-side illumination and horizontal longwave cloud absorption and emission, large differences exist at the interface of clouds and clear-sky regions around 1.5 km in height in Fig. 5i and in the position of cloud shadows.

Figure 6 shows the average profiles of 3D cloud-radiative effects for the four regions of the cyclone. In all regions, shortwave and longwave CRH is stronger in the 3D radiation calculation due to shortwave cloud-side illumination and longwave cloud-side cooling, respectively. There is a direct relationship between cloud-side illumination and the solar zenith angle (Fig. 6a; thin lines). In the 3D calculation, clouds receive more radiative energy from their sides at higher solar zenith angles, which increases shortwave cloud-radiative warming. Črnivec and Mayer (2019) also showed this direct relationship between cloud-side illumination and the solar zenith angle. The magnitude of the cloud-side cooling depends on the magnitude of the longwave CRH, such that the stronger the longwave CRH, the stronger the longwave cooling from the cloud sides.

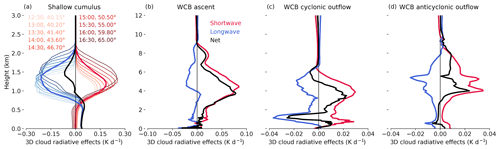
Figure 6 Average profiles of shortwave, longwave, and net 3D cloud-radiative effects for the four cyclone regions. The 3D cloud-radiative effects are calculated as the difference in domain mean CRH between 3D (MYSTIC) and 1D (MYSTIC-ICA) radiative transfer calculations. The thin lines in panel (a) show the 3D radiative effects for nine snapshots between 12:30 and 16:30 DLT, with the legend indicating the time and domain mean solar zenith angles for all snapshots. Note the different x axes in the panels.

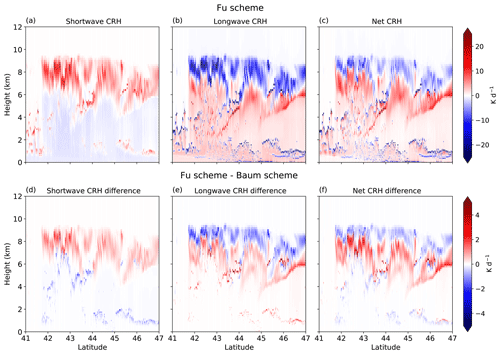
Figure 7 Cross-sections of (a) shortwave, (b) longwave, and (c) net CRH calculated with the ice optical parameterization of Fu in the WCB ascent region. Panels (d–f) show CRH differences between the ice scheme of Fu and the ice scheme of Baum with the general habit mixture (Fu – Baum). Cross-sections are shown at 14:30 DLT and at 3° longitude.

The 3D cloud-radiative effects are much weaker for WCB regions dominated by stratiform clouds than for the shallow cumulus region, which contains a lot of broken clouds (Fig. 6). This is expected due to the weak horizontal gradients of cloud optical properties and the small aspect ratio of the stratiform clouds in the WCB regions. For shallow cumulus clouds, the net 3D cloud-radiative effect is dominated by cloud-side longwave cooling (Fig. 6a). This could lead to a stronger radiative destabilization of clouds during both day and night. In contrast, for stratiform clouds in the WCB, shortwave cloud-side illumination dominates the daytime 3D cloud-radiative effects except for shallow liquid clouds in the boundary layer of the WCB cyclonic outflow region, where longwave cloud-side cooling becomes dominant (Fig. 6b–d). The stronger shortwave cloud-side illumination in the WCB regions is most likely due to the higher solar zenith angle at higher latitudes compared to that of the shallow cumulus region at lower latitudes. Although the incoming shortwave radiative fluxes are weaker at higher latitudes, shortwave cloud-side warming becomes stronger at higher zenith angles.

3.3 Impact of ice optical parameterization

We now quantify the impact of ice optical parameterization by comparing the CRH calculated with the ice optical parameterization of Fu and the more complex ice optical parameterization of Baum. The ice scheme of Baum includes three ice habits, which allows us to also assess the effect of different ice habits. We only consider clouds in the three WCB domains, where ice crystals are abundant.

The top row in Fig. 7 shows cross-sections of shortwave, longwave, and net CRH in the WCB ascent region for the ice scheme of Fu. The bottom row in Fig. 7 shows the CRH differences between the ice schemes of Fu and Baum with the general habit mixture. Fu results in stronger longwave and shortwave CRH than Baum does (Fig. 7d and e), with CRH differences reaching up to 20 % of the absolute values. As a result, Fu leads to stronger radiative destabilization in the longwave but stronger stabilization in the shortwave.

Figure 8 shows CRH differences between Fu and Baum. In all three WCB regions, longwave CRH and shortwave CRH are amplified in Fu compared to in Baum. The magnitude of the CRH differences depends on which ice crystal habit is chosen in the Baum scheme, with different impacts in the longwave and shortwave. In the longwave, the differences between Fu and Baum are the same for the general mixture and rough-aggregated habits but are smaller by a factor of 2 when the solid column habit is used in Baum. In the shortwave, the impact of the ice habit is much smaller. The stronger impact of the ice habit on the longwave compared to the shortwave CRH is an interesting aspect of our results.

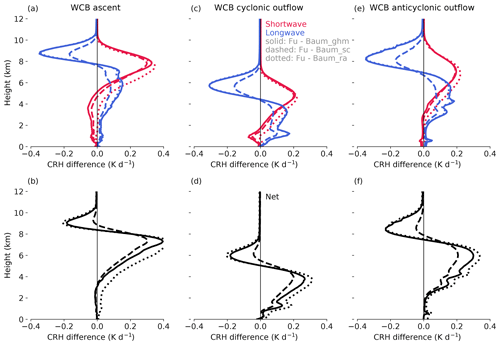
Figure 8 Impact of ice optical parameterization on time- and domain-averaged CRH in the three WCB regions. The CRH differences are calculated between the radiative transfer calculations and the ice schemes of Fu and Baum (Fu – Baum). The differences between Fu and Baum, along with general habit mixture (ghm), solid column (sc), and rough-aggregated (ra) habits, are shown using solid lines, dashed lines, and dotted lines as indicated in the legend.

Compared to Baum, Fu leads to stronger shortwave and longwave cloud-radiative warming in the middle and lower parts of the clouds and therefore to net cloud warming (Fig. 8, lower row). Although Fu leads to some increase in cloud-radiative cooling of the upper cloud parts, this suggests that the radiative destabilization of clouds within the WCB regions is smaller in Fu than in Baum.

3.4 Cloud horizontal heterogeneity and vertical overlap

We continue by quantifying the impact of cloud horizontal heterogeneity and vertical overlap. Both factors are not resolved at 2.5 km and therefore need to be parameterized. We calculate the CRH differences between the radiation calculations using the two types of homogeneous NWP clouds and the LEM clouds (Sect. 2.3; Fig. 3). For homogeneous grid-box clouds, an overlap assumption is not needed. For the homogeneous clouds with fractional cloud cover, we use a maximum-random overlap assumption.

The solid lines in the first row of Fig. 9 show CRH differences between homogeneous grid-box clouds and the LEM clouds, decomposed into longwave and shortwave components. In all regions, the magnitude of the longwave and shortwave CRH profiles is overestimated when homogeneous grid-box clouds are used, with the longwave CRH being more strongly affected than the shortwave CRH and the largest differences occurring in shallow cumulus clouds.

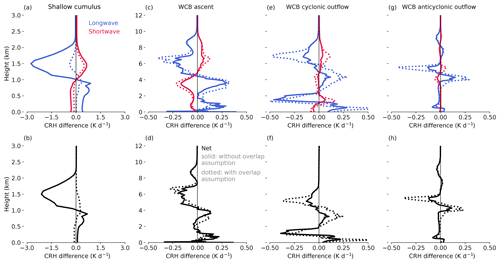
Figure 9 Impact of cloud horizontal heterogeneity and vertical overlap on CRH, which are not resolved at a 2.5 km horizontal resolution. The CRH differences are calculated between the LEM reference calculation and the radiative transfer calculations for the homogeneous NWP clouds (NWP – LEM), with solid lines for the homogeneous grid-box clouds (without overlap assumption) and dotted lines for the homogeneous clouds with fractional cloud cover (with overlap assumption). Note the different x and y axes for panels (a) and (b).

The second row of Fig. 9 compares the impact of the two types of homogeneous clouds. When the overlap scheme is used for the homogeneous clouds with fractional cloud cover, the differences in CRH between the NWP and LEM clouds are strongly reduced in the shallow cumulus region, from −2 to 0.5 K d⁻¹. This illustrates a clear positive impact of taking into account cloud fraction and partial overlap for these clouds and that treating these clouds as grid-box clouds at a 2.5 km resolution is problematic.

In the three WCB regions, cloud vertical overlap assumption has a smaller impact on CRH because the cloud fraction is higher. However, in contrast to the shallow cumulus region, taking the cloud overlap assumption into account has a detrimental effect and in fact increases the CRH differences for shortwave, longwave, and net (Fig. 9c–h). This supports the idea that clouds in the WCB regions can be treated as grid-box clouds at a 2.5 km resolution for radiative purposes because there is no obvious benefit of taking into account the cloud fraction and vertical overlap assumption.

4 Relative importance of uncertainties

In the previous sections, we have assessed the individual impacts of the following four factors on CRH: 3D cloud-radiative effects, ice optical parameterization, cloud horizontal heterogeneity, and cloud vertical overlap. In this section, we characterize the relative importance of these four factors for extratropical cyclones, with the hope that this can guide efforts to improve CRH in models. As part of this characterization, we distinguish between mean uncertainties in spatial scales of around 500 km, which is approximately the size of the LEM domain, and local uncertainties that arise on the scale of the horizontal grid resolutions. For uncertainties due to 3D cloud-radiative effects and ice optical parameterization, the scale of the horizontal grid resolution is 300 m, and for the uncertainties due to cloud horizontal heterogeneity and cloud vertical overlap, the scale of the horizontal grid resolution is 2.5 km.

For the mean uncertainties, we compute the absolute mean difference,

$$\begin{array}{}\text{(2)}& \mathit{\delta }{\text{CRH}}_{\text{mean}}=|{\stackrel{\mathrm{‾}}{\text{CRH}}}_a-{\stackrel{\mathrm{‾}}{\text{CRH}}}_b|,\end{array}$$

where the bars represent the average over time and the domain and the subscripts a and b indicate different radiative transfer calculations. This means that the mean uncertainties are obtained from the absolute values of the figures shown in Sect. 3.

For the local uncertainties, we compute the mean absolute difference by first computing the absolute CRH differences at all grid points and then averaging over time and the domain,

$$\begin{array}{}\text{(3)}& \mathit{\delta }{\text{CRH}}_{\text{local}}={\displaystyle \frac{\mathrm{1}}{n\cdot t}}\sum _{j=\mathrm{1}}^t\sum _{i=\mathrm{1}}^n\left|{\text{CRH}}_a\right(i,j)-{\text{CRH}}_b(i,j\left)\right|.\end{array}$$

n is the number of horizontal grid points i at each vertical layer, and t is the number of time steps j. To derive the local uncertainties due to horizontal cloud heterogeneity and vertical overlap, we coarse-grain the LEM CRH to the same horizontal resolution as the NWP CRH.

Figure 10 shows mean uncertainties by means of stacked bar plots in altitude intervals of 2 km calculated based on Eq. (2). For shallow cumulus clouds in the boundary layer between 0 and 2 km, the largest source of mean uncertainty is cloud horizontal heterogeneity without overlap assumption (Fig. 10a–c; blue bars). Allowing for partial overlap of homogeneous clouds with cloud fraction significantly reduces the mean uncertainty (cf. green and blue bars in Fig. 10a–c). The mean uncertainty due to 3D cloud-radiative effects is about half of the uncertainty due to cloud horizontal heterogeneity when vertical overlap is considered.

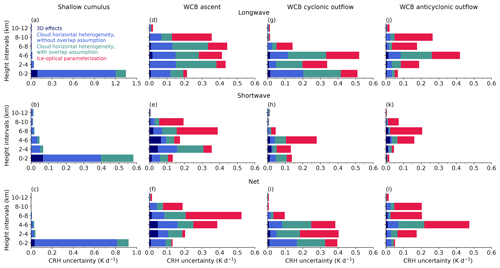
Figure 10 Mean uncertainties in CRH diagnosed as the absolute difference in domain and time mean CRH between different radiative transfer calculations. Uncertainties are decomposed into shortwave, longwave, and net. Uncertainties are computed as mass-weighted averages over 2 km altitude intervals. For the uncertainty due to the ice optical parameterization, the difference between the ice schemes of Fu and Baum with the general habit mixture is used. The contribution of each factor is given by the horizontal length of its colored bar. Note the different x axes in the panels.

For clouds in the WCB ascent region, cloud horizontal heterogeneity has a significant impact on the mean uncertainty at all levels and dominates the CRH uncertainty in the boundary layer (Fig. 10d–f; blue bars). Apart from the boundary layer and in contrast to shallow cumulus clouds, considering the vertical overlap assumption increases the mean uncertainty (cf. green and blue bars in Fig. 10d–f). Ice optical parameterization dominates the mean uncertainty in net CRH in the middle and upper levels above 6 km in altitude (Fig. 10f). The 3D cloud-radiative effects contribute relatively little, except at altitudes between 2 and 6 km in the shortwave and the net.

The relative importance of the four factors for the mean uncertainties in the WCB cyclonic outflow region is similar to that in the WCB ascent region (Fig. 10g–i). The ice optical parameterization contributes significantly to the mean uncertainty in the middle and upper levels, while cloud horizontal heterogeneity dominates the mean uncertainty in the boundary layer. The vertical overlap assumption increases the mean uncertainty, and the impact of the 3D cloud-radiative effects is small. The mean uncertainty in the WCB anticyclonic outflow region is dominated by the ice optical parameterization, and the impact of cloud horizontal heterogeneity and vertical overlap is much weaker compared to the other regions of the cyclone, except those between 4 and 6 km in altitude (Fig. 10j–l).

Now we turn to local uncertainties in CRH. These are illustrated in Fig. 11 for net CRH. For comparison of mean and local uncertainties, Fig. 11 includes the mean net CRH uncertainties from Fig. 10 only for values larger than 0.05 K d⁻¹, shown as gray-hatched bars. In contrast to the mean uncertainties, the impact of 3D cloud-radiative effects is much stronger at the scale of the horizontal grid resolution of 300 m. Except for the WCB anticyclonic domain, cloud horizontal heterogeneity dominates local uncertainties at the boundary layer between 0 and 2 km and mid-levels between 2 and 8 km in all regions of the cyclone. As for the mean uncertainties, taking into account the vertical overlap assumption reduces the local uncertainties for shallow cumulus clouds but slightly increases them for stratiform clouds in the WCB regions. Local uncertainties due to 3D cloud-radiative effects, cloud horizontal heterogeneity, and vertical overlap are much larger compared to their mean uncertainties in all four regions of the cyclone. However, the ice optical parameterization has similar impacts on local and mean uncertainties. This shows that 3D cloud-radiative effects, cloud horizontal heterogeneity, and vertical overlap have a much stronger impact on CRH locally than on the domain mean.

Figure 11 Same as Fig. 10 but for local uncertainties in net CRH. For comparison, the mean net CRH uncertainties from Fig. 10 are superimposed as gray-hatched bars. Mean uncertainties smaller than 0.05 K d⁻¹ are not shown as they would not be visible in the plot. Note the different x axes in the panels.

To understand the relative importance of CRH uncertainties at different horizontal spatial scales and for the dynamics of extratropical cyclones, we coarse-grain CRH from different radiative transfer calculations from their original horizontal resolution to horizontal resolutions equivalent to 2.5, 5, 10, 50, 100, and 500 km, which is approximately the spatial extent of the LEM domains. We calculate the CRH uncertainty at different spatial scales x by computing the mean absolute difference in net CRH between different radiative transfer calculations from different sets of coarse-grained CRH and average them over time and the domain,

$$\begin{array}{}\text{(4)}& \mathit{\delta }{\text{CRH}}_x={\displaystyle \frac{\mathrm{1}}{n\cdot t}}\sum _{j=\mathrm{1}}^t\sum _{i=\mathrm{1}}^n\left|{\text{CRH}}_{x,a}\right(i,j)-{\text{CRH}}_{x,b}(i,j\left)\right|.\end{array}$$

Here, x is the horizontal resolution of the coarse-graining, the subscripts a and b indicate different radiative transfer calculations, n is the number of horizontal grid points i at each vertical layer for different resolutions, and t is the number of time steps j. The CRH uncertainty calculated from Eq. (4) is an intermediate between the mean and the local CRH uncertainties described earlier, such that at horizontal resolutions of 300 m and 2.5 km this equation is equivalent to Eq. (3), and at a resolution of 500 km, the equation is equivalent to Eq. (2). For the shallow cumulus domain, where clouds are present only in the boundary layer, we apply a mass-weighted vertical average to the CRH uncertainties between 0 and 2 km in altitude, but for the WCB domains, we apply the average between 0 and 12 km in altitude (Fig. 12).

Figure 12 shows that in all regions of the cyclone, the net CRH uncertainty due to 3D cloud-radiative effects and cloud horizontal heterogeneity with overlap assumption decrease with increases in the horizontal scale. In the WCB regions, these uncertainties decrease more rapidly than the uncertainty due to the ice optical parameterization (cf. green and dark-blue lines with red lines in Fig. 12b–d). This analysis indicates that while the CRH uncertainty due to 3D cloud-radiative effects is large at horizontal resolutions of hundreds of meters, its spatial extent is limited and it becomes less relevant at larger spatial extents. The uncertainty due to cloud horizontal heterogeneity shows a similar pattern but is larger than the uncertainty due to 3D cloud-radiative effects. In contrast, the uncertainty due to the ice optical parameterization is more or less constant as a function of horizontal scale in the WCB regions and dominates the uncertainty at spatial scales of 100 km or more. This is due to the large-scale stratiform ice clouds that cover entire domains in the WCB region of the cyclone, and therefore nearly the same level of uncertainty occurs over the entire domain.

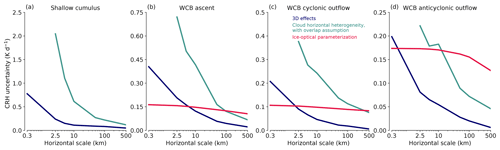
Figure 12 Net CRH uncertainties as a function of horizontal scale from 300 m to approximately 500 km for all LEM domains. Uncertainties are computed as mass-weighted vertical averages between 0–2 and 0–12 km altitude intervals for shallow cumulus and WCB regions, respectively. For the uncertainty due to the ice optical parameterization, the CRH difference between the ice schemes of Fu and the ice scheme of Baum with the general habit mixture is used. Note the different y axes in the panels.

Our analysis suggests that large-scale changes in the dynamics of the cyclone are more susceptible to CRH uncertainties due to cloud horizontal heterogeneity (assuming resolved clouds at the horizontal resolution of the NWP model) and ice optical parameterization than due to 3D cloud-radiative effects.

5 Discussion and conclusion

Recent studies have demonstrated that cloud-radiative heating and cooling within the atmosphere (hereafter referred to as CRH) are important for the dynamics and predictability of extratropical cyclones. However, CRH is uncertain in numerical weather prediction (NWP) and climate models, and these uncertainties may have systematic effects on model predictions of extratropical cyclones. This motivates us here to study CRH and its uncertainty within extratropical cyclones. To this end, we simulate an idealized extratropical cyclone with the ICON atmosphere model at a horizontal resolution of 2.5 km and focus on CRH within four regions of the cyclone with distinct cloud patterns: shallow cumulus clouds southwest of the cyclone center, deep clouds in the ascending region of the warm conveyor belt (WCB), stratiform low- and mid-level clouds in the WCB cyclonic outflow, and high stratiform ice clouds in the WCB anticyclonic outflow. For these four regions, we perform large-eddy-model (LEM) simulations at a horizontal resolution of 300 m, which we use to drive offline radiative transfer calculations. This provides a framework, for the first time, to assess and compare uncertainty in CRH due to four factors within an extratropical cyclone: 3D cloud-radiative effects, ice optical parameterization, cloud horizontal heterogeneity, and cloud vertical overlap. Since we can assume that clouds from the LEM simulations are perfectly known for the purpose of radiative transfer calculation, we quantify the last two factors by coarse-graining the LEM clouds to a horizontal resolution of 2.5 km, that of the NWP model. We create two sets of NWP homogeneous clouds, with and without cloud fraction. By doing so, we quantify to what extent ignorance of the cloud sub-grid variability at scales below 2.5 km affects CRH.

We find that 3D cloud-radiative effects are large at the scale of the horizontal grid resolution of 300 m but negligible on larger spatial scales of hundreds of kilometers. The 3D cloud-radiative effects are also more important for shallow cumulus clouds than for clouds within the WCB. Horizontal photon transport within the cloud and from the cloud sides is small in the three WCB regions, where more uniform stratiform clouds prevail. These results are consistent with previous findings that 3D cloud-radiative effects are small for stratiform clouds (Črnivec and Mayer, 2021) but important for the dynamics of shallow cumulus clouds (Jakub and Mayer, 2016).

The uncertainty in CRH due to different ice optical parameterizations is substantial in the WCB of the cyclone. We show that using the more complex ice optical parameterization of Baum leads to weaker shortwave and longwave CRH. Our analysis shows that the ice optical parameterization is the largest source of uncertainty in spatial scales of 500 km in the upper troposphere where ice clouds prevail. The uncertainty due to ice optical parameterization is also rather uniform in space, which suggests that it can affect the cyclone by modulating large-scale radiative heating. Our findings are consistent with the results of Zhao et al. (2018), who found that the ice scheme of Baum has a weaker effect on shortwave cloud-radiative effects compared to the ice scheme of Fu. Zhao et al. (2018) showed that the Baum scheme decreases static stability and increases vertical motion in the midlatitudes. An important potential implication of this result that should be tested in future work is to what extent this might enhance latent heating in the WCB ascent region and alter the dynamics of the cyclone (Keshtgar et al., 2023). Our expectation is in line with studies showing that perturbations on a larger spatial scale are more effective for baroclinic error growth (e.g., Sun and Zhang, 2016). Recently, Lloveras et al. (2023) showed that small-scale perturbations, even with large amplitudes, have a negligible impact on the dynamics of the cyclone and the error growth near the tropopause compared to larger-scale perturbations with smaller amplitudes.

Cloud horizontal heterogeneity contributes significantly to CRH uncertainty in all regions of the cyclone. This is consistent with previous findings that when cloud sub-grid variability is neglected, both longwave CRH and shortwave CRH are overestimated (e.g., Črnivec and Mayer, 2019). The impact is strong for shallow cumulus clouds, but it is much smaller for the stratiform clouds in the WCB. Including the vertical overlap assumption significantly improves the simulation of CRH for shallow cumulus clouds but in fact slightly degrades CRH for clouds in the WCB since the maximum-random overlap assumption misrepresents the vertical arrangement of cloud layers in sheared flows, and a more complex form of the overlap assumption would be needed (e.g., Giuseppe and Tompkins, 2015). The comparison between the impact of cloud horizontal heterogeneity and cloud vertical overlap shows that for shallow cumulus clouds, vertical overlap has a stronger impact on CRH than cloud horizontal heterogeneity. In contrast, for stratiform clouds in the WCB, vertical overlap has a weaker effect on CRH compared to cloud horizontal heterogeneity. An interesting corollary of our work is that for extratropical cyclones, treating clouds as grid-box quantities in kilometer-scale models with resolutions of around 2 km appears to be a reasonable choice because schemes for cloud cover and vertical overlap themselves can act as sources of uncertainty that are rarely quantified. This supports the approach taken by Hohenegger et al. (2023) for the ICON-Sapphire kilometer-scale model, where they decided to remove the cloud cover scheme and treat grid boxes as either entirely cloudy or entirely cloud-free.

Our study indicates that improving the representation of ice optical properties is particularly relevant for the dynamics of extratropical cyclones. This is for several reasons. First, for the baroclinic error growth, the spatial scale of the uncertainty is more important than the amplitude of the uncertainty (e.g., Lloveras et al., 2023). Although 3D cloud-radiative effects are large at the scales of LEM grid resolution and have been shown to affect the organization of subtropical low-level clouds, their spatial extent is limited. Second, cloud sub-grid variability and 3D cloud-radiative effects can be taken into account in existing state-of-the-art radiation schemes such as TripleClouds (Črnivec and Mayer, 2021) and the Speedy Algorithm for Radiative Transfer through Cloud Sides (SPARTACUS;  Hogan et al., 2016). Third, the parameterization of ice optical properties represents an important source of uncertainty and dominates the CRH uncertainty at larger scales.

Although advances in radiation solvers can account for both 3D radiative effects and cloud sub-grid variability, the lack of knowledge about the shape and surface roughness of ice particles continues to introduce large variability in CRH and remains a critical challenge for better representation of ice optical properties in models. Future work in the direction of ice optical properties should also address the problem that in many current models including ICON, the ice crystal effective radii are not treated consistently in the microphysics and radiation schemes (Sullivan and Voigt, 2021), and longwave cloud scattering is neglected (Fan et al., 2023). In view of our results, we believe that future studies should focus on the impact that uncertainties in the ice optical properties have on the dynamics and predictability of extratropical cyclones.