How does riming influence the observed spatial variability of ice water in mixed-phase clouds?

Observations show that the ice water content (IWC) in mixed-phase clouds (MPCs) tends to occur in clusters. However, it is not sufficiently understood which ice crystal formation and growth processes play a dominant role in IWC clustering in clouds. One important ice growth process is riming, which occurs when liquid water droplets freeze onto ice crystals upon contact. Here we use airborne measurements of MPCs at mid- and high-latitudes to investigate the spatial variability of ice clusters in clouds and how this variability is linked to riming. We use data from the IMPACTS (mid-latitudes) and the HALO-(AC)³ (high-latitudes) aircraft campaigns, where spatially and temporally colocated cloud radar and in situ measurements were collected. We derive riming and IWC by combining cloud radar and in situ measurements. Ice cluster scales in clouds are quantified using pair correlation functions.

During all analyzed flight segments, riming is responsible for 66 % and 63 % of the total IWC during IMPACTS and HALO-(AC)³, respectively. In mid-latitude MPCs, riming does not significantly change IWC cluster scales but increases the probability of cluster occurrence. In cold-air-outbreak MPCs observed during HALO-(AC)³, riming leads to additional in-cloud IWC clustering at spatial scales of 3–5 km due to the presence of mesoscale updraft features. An increased liquid water path might increase the effect, but it is not a necessary criterion. These results can be used to evaluate and constrain models' representations of MPCs.

1 Introduction

At mid-latitudes and high latitudes, most precipitation stems from ice-containing clouds (Mülmenstädt et al., 2015), which are a crucial component of the Earth's weather and climate systems. In mixed-phase clouds (MPCs), ice particles and supercooled liquid droplets coexist in a thermodynamically unstable state down to temperatures of about −38 °C. The mass and the ratio of ice and liquid particles play a critical role in not only precipitation processes but also cloud lifetime, radiative budget (Sun and Shine, 1994; Shupe and Intrieri, 2004; Turner, 2005), and climate feedbacks (Choi et al., 2014; Bjordal et al., 2020).

Numerical forecast and climate models often fail to realistically predict or reproduce MPC properties, lifetimes, and precipitation amounts (Morrison et al., 2012, 2020; Ong et al., 2024; Connelly and Colle, 2019). The misrepresentation of MPCs and ice clouds has been suggested as a major contributor to the uncertainty in Coupled Model Intercomparison Project version 6 (CMIP6) climate model predictions (e.g., Bock et al., 2021). This is partly related to a poor understanding of ice formation and growth processes in MPCs (Korolev et al., 2017). Their representations are therefore likely incomplete, even in sophisticated cloud microphysics schemes (e.g., Cao et al., 2023), such as the predicted particle properties (P3) scheme proposed by Morrison and Milbrandt (2015). Gaps in our understanding of the dominant ice processes hinder progress in the representation of MPCs in models (Morrison et al., 2012).

An important ice growth process is riming, which describes the process by which supercooled droplets freeze onto ice particles after contact. Riming efficiently converts liquid to ice and typically results in increased particle mass, density, and fall speed (Heymsfield, 1982; Erfani and Mitchell, 2017; Seifert et al., 2019). Although riming can theoretically significantly increase ice water content (IWC) in MPCs, it is unclear how much it actually contributes to ice mass and further to snowfall amounts on the ground with different studies reaching different conclusions (Harimaya and Sato, 1989; Moisseev et al., 2017; Kneifel and Moisseev, 2020; Fitch and Garrett, 2022; Waitz et al., 2022).

Cloud properties are determined not only by the mass and the ratio of liquid and ice particles but also by their spatial distribution. Observations show that ice particles and liquid droplets in MPCs are often heterogeneously mixed, leading to the formation of hydrometeor clusters (Korolev et al., 2003; Field et al., 2004; Korolev and Milbrandt, 2022). The ability to quantify spatial scales of IWC clustering would allow for model evaluation beyond comparison of IWC distributions. Furthermore, it is poorly understood which microphysical processes lead to IWC clustering at which spatial scales. While quantifying spatial scales of cloud particle clusters has been the focus of previous studies, most have focused on liquid-phase clouds, analyzing liquid droplet clustering on small scales below 1 m (Kostinski and Shaw, 2001; Shaw et al., 2002; Baker and Lawson, 2010), where turbulence plays a major role in clustering (Wood et al., 2005; Saw et al., 2012a, b). Studies of MPCs suggest that ice clustering occurs at different spatial scales than liquid clusters (Korolev and Milbrandt, 2022; Deng et al., 2024). Deng et al. (2024) propose that ice clusters – defined as regions with enhanced ice particle number or IWC – on larger scales of a few kilometers dominate the inhomogeneity of the ice distribution within clouds. However, their analysis is based on in situ data from a single case over China, and it is unclear whether their findings are representative of different types of MPCs.

Accurate in situ measurements of IWC remain challenging (Heymsfield et al., 2010; Baumgardner et al., 2017; Tridon et al., 2019), although in situ cloud probes can provide reliable particle size distribution (PSD) data (Korolev et al., 2013; Moser et al., 2023b). Lacking IWC measurements, Deng et al. (2024) calculated IWC from PSD observations, assuming that ice particle mass as a function of ice particle size follows a power law relationship. Because it is difficult to derive size-resolved ice particle densities from in situ observations alone, Deng et al. (2024) used constant mass size parameters from Heymsfield et al. (2010). Therefore, their analysis captures IWC variability due to ice number concentration and size but not ice particle density, which is commonly linked to riming (Erfani and Mitchell, 2017; Seifert et al., 2019).

The combination of colocated cloud radar and in situ PSD data shows great potential to provide better insight into microphysical processes (Nguyen et al., 2022; Mróz et al., 2021). It also allows the estimation of IWC by inferring ice particle density changes due to riming (Maherndl et al., 2024). In this way, IWC variability driven by riming-induced changes in ice particle density can be studied. In recent years, the synergistic use of both remote sensing and in situ instrumentation during airborne campaigns has become more common (Houze et al., 2017; McMurdie et al., 2022; Nguyen et al., 2022; Kirschler et al., 2023; Sorooshian et al., 2023; Wendisch et al., 2024; Maherndl et al., 2024).

Here we use colocated cloud radar and in situ cloud probe observations in MPCs collected during the IMPACTS (McMurdie et al., 2022) and the HALO-(AC)³ (Wendisch et al., 2024) aircraft campaigns. The focus of IMPACTS was to study precipitation variability during wintertime snowstorms. The main objective of the HALO-(AC)³ campaign was to study Arctic air mass transformations during warm air intrusions and marine cold air outbreaks (MCAOs). During both campaigns, two aircraft flew in an approximately vertically stacked coordinated pattern to collect spatially and temporally colocated radar and in situ data.

We aim to achieve the following goals:

1. to quantify spatial scales of ice clusters in MPCs observed during the IMPACTS (mid-latitude winter storms) and HALO-(AC)³ (Arctic MCAO clouds) aircraft campaigns,

2. to characterize spatial scales at which riming enhances in-cloud ice clustering and link to drivers of riming,

3. to compare ice cluster scales and the impact of riming for mid- and high-latitude MPCs.

Because we aim to compare IWC variability in MPCs at different latitudes, we use data from both aircraft campaigns. IMPACTS data were collected during four flights over the US East Coast and the Midwest. For HALO-(AC)³, we use data from three flights over the Fram Strait west of Svalbard. We compare the contribution of riming to IWC to other ice formation processes in absolute terms and with respect to the spatial scales of ice clustering using the pair correlation function. The paper is organized as follows. Section 2 presents the airborne datasets we use to study riming and IWC variability. Section 3 illustrates the methods we use to quantify riming, derive IWC, and analyze scales of IWC variability in clouds. The main results are presented in Sect. 4. In Sect. 5 we summarize and discuss our findings.

2 Data

2.1 Airborne campaigns: IMPACTS and HALO-(AC)³

The Investigation of Microphysics and Precipitation for Atlantic Coast-Threatening Snowstorms (IMPACTS, McMurdie et al., 2022) campaign was a field campaign sponsored by the National Aeronautics and Space Administration (NASA) to study wintertime snowstorms with a focus on precipitation variability in US East Coast cyclones. Here, we use data collected during the winter of 2020, where a variety of storms from the Midwest to the US East Coast were sampled.

The German Research Foundation (DFG) funded the field campaign HALO-(AC)³ (Wendisch et al., 2024, HALO, High Altitude and Long Range Research Aircraft – (AC)³ Project on Arctic Amplification Climate Relevant Atmospheric and Surface Processes and Feedback Mechanisms; see https://halo-ac3.de/, last access: 8 October 2024), which took place in March and April 2022 and aimed to investigate Arctic air mass transformations. In this study, we analyze data collected during MCAO conditions over the Fram Strait west of Svalbard.

Common to both aircraft campaigns was the use of two aircraft to perform colocated in situ and remote sensing measurements. During IMPACTS, the ER-2 aircraft flew above clouds carrying a variety of passive and active remote sensing instruments, including multi-frequency Doppler radars. Simultaneously, the NASA P-3 aircraft collected measurements of microphysical cloud properties in situ while flying inside clouds. During HALO-(AC)³, the AWI aircraft Polar 5 and Polar 6 performed similar measurements. Polar 5, equipped with a W-band radar among other remote sensing instruments, flew above Polar 6, which performed in situ measurements in clouds.

However, both campaigns covered different observation areas and sampled at different frequency rates, i.e., different spatial resolutions. With a typical flight speed of 200 (150) m s⁻¹, the ER-2 (P-3) covered a larger spatial scale with a coarser resolution than Polar 5 and Polar 6, which flew at 60–80 m s⁻¹. While the ER-2 and Polar 5 flew at a constant altitude of 20 and 3 km, respectively, P-3 and Polar 6 sampled at different altitudes up to 8.5 and 3 km, respectively. In this study, we investigate data collected during the flight days listed in Table 1. We selected these days because of the good colocation (which we define as maximum spatial offsets of 5 km and temporal offsets of 5 min; see Sect. 2.4) between the respective remote sensing and in situ aircraft and because of data availability. Figure 1 shows all coordinated flight tracks.

Table 1 Overview of analyzed flight days including campaign, measurement area, and synoptic situation.

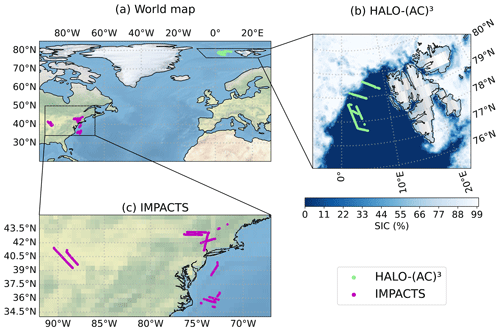
Figure 1 Flight tracks of (a) all analyzed coordinated flight segments and a zoomed-in view of the (b) HALO-(AC)³ and (c) IMPACTS measurement areas. In (b), the sea ice concentration (SIC) derived from the Advanced Microwave Scanning Radiometer 2 (AMSR2) onboard the GCOM-W1 satellite on 1 April 2022 is shaded in blue.

2.2 Instruments

The equivalent radar reflectivity factor Z_e was measured by multiple radars during IMPACTS: X-band (9.6 GHz, EXRAD, Heymsfield et al., 1996, 2022), Ku and Ka band (13.6 and 35.6 GHz, HIWRAP, Li et al., 2016, 2022), and W band (94 GHz, CRS, McLinden et al., 2021, 2022). EXRAD consists of a nadir-pointing beam and a conically scanning beam, but only the nadir-pointing beam is used in this study. EXRAD, HIWRAP, and CRS sampled at 4, 2, and 4 Hz with vertical resolutions of 19, 26, and 26 m, respectively. EXRAD, HIWRAP Ku band, HIWRAP Ka band, and CRS have sensitivity limits of −15, 0, −5, and −28 dBZ at 10 km range, respectively. During HALO-(AC)³, a W-band radar (94 GHz, MiRAC-A, Mech et al., 2019, 2024a) was deployed. MiRAC-A was mounted with a 25° backwards inclination sampled at 1 Hz, and Z_e data are available with 5 m vertical resolution. For the scattering calculations performed within this study, the 25° inclination is negligible (not shown). MiRAC-A has a sensitivity limit of about −40 dBZ at 3 km range. For both campaigns, Z_e data are quality controlled and corrected for instrument orientation and aircraft motion (for MiRAC-A; see Mech et al., 2019). Uncertainties in Z_e due to radar calibration are estimated to be below 1 and 0.5 dB for IMPACTS and HALO-(AC)³ data, respectively (Finlon et al., 2022; Mech et al., 2019). MiRAC-A Z_e is corrected for attenuation due to liquid water content (LWC) as described in Maherndl et al. (2024); CRS Z_e is as described in Finlon et al. (2022). Attenuation due to water vapor and atmospheric gases is below 0.5 dB for all radars and is therefore neglected.

During HALO-(AC)³, brightness temperature T_B measurements at 89 GHz were collected and are used to derive the liquid water path (LWP). Differences in T_B for clear-sky and cloudy conditions are used to retrieve LWP over the open ocean via a regression approach (Ruiz-Donoso et al., 2020; Maherndl et al., 2024). Lidar measurement of backscattered intensities at 532 nm (parallel and perpendicular polarized) and 355 nm (non-polarized; Stachlewska et al., 2010) are used to derive cloud top height (CTH) during HALO-(AC)³ (Mech et al., 2022a, 2024b; Schirmacher et al., 2023; Maherndl et al., 2024).

Cloud particle observations obtained with a variety of cloud probes cover a size range from 2 µm to about 2 cm for IMPACTS and 2.8 µm to 6.4 mm for HALO-(AC)³. For IMPACTS, we use data from a fast-cloud droplet probe (Fast-CDP, 2–50 µm, Lawson et al., 2017), a two-dimensional stereo (2D-S, Lawson et al., 2006) probe (10–2000 µm with a pixel resolution of 10 µm), and one horizontally oriented and one vertically oriented high-volume precipitation spectrometer version 3 (HVPS-3, Lawson et al., 1998) probe (0.3–19.2 mm, pixel resolution of 150 µm). For HALO-(AC)³, we use data from a cloud droplet probe (CDP, 2.8–50 µm, Lance et al., 2010), a cloud imaging probe (CIP, 15–960 µm, pixel resolution of 15 µm, Baumgardner et al., 2001), and a precipitation imaging probe (PIP, 103–6400 µm, pixel resolution of 103 µm, Baumgardner et al., 2001). Here, we use merged particle size distribution (PSD) data from the respective campaign (Bansemer et al., 2022; Moser et al., 2023a), which are derived from the instruments listed above. As in Moser et al. (2023b) and Maherndl et al. (2024), we assume all particles larger than 50 µm in MPCs to be ice particles. As in Maherndl et al. (2024), we only include data up to −1 °C to avoid melting ice particles, which are not represented well in the scattering simulations that we perform. In addition, we manually looked through in situ images of all remaining flight segments and removed two IMPACTS segments where we could identify supercooled droplets larger than 50 µm. LWC was measured in situ with a King probe (King et al., 1978) and a Nevzorov probe (Korolev et al., 1998; Lucke et al., 2022, 2024) during IMPACTS and HALO-(AC)³, respectively. Due to the poor data availability¹ and high uncertainties in IWC measurements, IWC is calculated from the PSD as described in more detail in Sect. 3.2. For more details on IMPACTS and HALO-(AC)³ instrumentation and data processing, we refer the reader to McMurdie et al. (2022) and Moser et al. (2023b), Mech et al. (2022a), and Maherndl et al. (2024), respectively.

2.3 Synoptic situation

In this section, we give a brief overview of the typical synoptic situations encountered during the different field campaigns to provide context for the types of MPCs that we analyze. We use an example flight segment for each campaign, which we describe in detail in Sects. 4.1.1 and 4.1.2.

During IMPACTS, a variety of mid-latitude wintertime storms in different development stages were observed. The focus was on the observation of banded precipitation structures. Observations range from a relatively weak and warm developing Atlantic low systems without major banding structures (1 February 2020) to rapidly deepening cyclones with significant snowfall and snow bands (5 February 2020). The majority of the measurements stem from the Midwest and close to the US East Coast (both over ocean and land), ranging up to southern parts of Canada (Fig. 1). The coordinated ER-2 and P-3 flights on 5 February sampled an elevated warm front over shallow, pre-existing cold air as a low-pressure center developed over Louisiana and Mississippi. The developing circulation around the low produced a low-level northeasterly flow across the Midwest. Precipitation formed as rain (in the south) and snow (in the north) due to the overflow of warm, moist air from the south. During the observation period, snow band structures were observed.

Measurements during HALO-(AC)³ were conducted west of Svalbard over both open ocean and sea ice. However, clouds over the sea ice were very thin to non-existent during all three flights used here. Northerly to northeasterly flow brought cold air masses from the sea ice of the higher Arctic to the comparatively warm open ocean. This led to the formation of roll cloud streets. On 1 April 2022, the MCAO was especially strong, meaning that the difference between the potential temperature at sea surface and the potential temperature at 850 hPa was large (about 8 K). On 28 March and 4 April 2022, weaker MCAO conditions were observed due to convection of air masses from North America over Siberia (28 March) or the central Arctic (4 April) to Svalbard (Walbröl et al., 2024).

2.4 Colocation

To combine in situ and remote sensing observations of the two aircraft, we use the same colocation criterion as in Maherndl et al. (2024), which is also extended to the IMPACTS data. In summary, following Chase et al. (2018) and Nguyen et al. (2022), the closest radar data point to the in situ measurements is selected. Each 1, 2, or 4 Hz radar aircraft (Polar 5 and ER-2) data point is matched with the spatially closest in situ aircraft (Polar 6 and P-3) data point within a 5 min time window. We consider data with a maximum spatial offset of 5 km to be “colocated”. The closest radar range gate to the flight altitude of the in situ aircraft is chosen. Averaging over certain height ranges did not lead to significant improvements.

Rolling averages were applied to Z_e and in situ data to obtain more robust statistics for the latter. To cover approximately the same spatial scales, averaging windows of 10 and 30 s are chosen for IMPACTS and HALO-(AC)³, respectively. With typical flight speeds of 180–200 m s⁻¹ and 60–80 m s⁻¹ during IMPACTS and HALO-(AC)³, respectively, this corresponds to spatial scales of 1.8–2.0 km and 1.8–2.4 km, respectively. We assume the in situ measurement is representative of the entire matched radar volume. Possible implications of this assumption for the riming retrieval are discussed in Maherndl et al. (2024).

3 Methods

3.1 Retrieving ice particle riming

We use the normalized rime mass M (Seifert et al., 2019) to describe riming. M is defined as the particle's rime mass m_rime divided by the mass of a size-equivalent spherical graupel particle m_g, where we assume a rime density of ρ_rime=700 kg m⁻³:

$$\begin{array}{}\text{(1)}& M={\displaystyle \frac{m_{\text{rime}}}{m_{\mathrm{g}}}},\end{array}$$

where

$$\begin{array}{}\text{(2)}& m_{\mathrm{g}}={\displaystyle \frac{\mathit{\pi }}{\mathrm{6}}}{\mathit{\rho }}_{\text{rime}}{D}_{\text{max}}^{\mathrm{3}}.\end{array}$$

The maximum dimension D_max is defined as the diameter of the smallest circle encompassing the cloud particle in meters and is used to parameterize particle sizes.

We retrieve M using the two methods introduced in Maherndl et al. (2024), which are termed the combined method and the in situ method. The methods in Maherndl et al. (2024) were developed for HALO-(AC)³, but we apply them to IMPACTS data with slight adjustments due to different instrumentation. In the following, we give a brief explanation of both methods and describe the adjustments for IMPACTS data. For more details, we refer the reader to Maherndl et al. (2024).

The combined method derives M along the flight track of the in situ airplane from colocated PSD and radar reflectivity Z_e measurements. It therefore relies on colocated in situ and remote sensing flights. An optimal estimation (Rodgers, 2000) algorithm is used to retrieve M by matching simulated radar reflectivities Z_e obtained from observed in situ PSD with the spatially and temporally closest measured Z_e. As forward operator we use the Passive and Active Microwave radiative TRAnsfer tool (PAMTRA, Mech et al., 2020), which includes empirical relationships Maherndl et al. (2023a) for estimating particle scattering properties as a function of M. For IMPACTS, the combined method is applied (separately) to X-, Ku-, Ka-, and W-band Z_e (see Sect. 4.1.3). As in Maherndl et al. (2024), we use the riming-dependent mass–size parameter relation for dendrites from Maherndl et al. (2023a) that were estimated for different degrees of riming, i.e., M values. Dendrites were chosen because 86.2 % of the data during the analyzed IMPACTS segments are within the temperature ranges of −20 to −10 °C and −5 to 0 °C, where plate-like growth of ice crystals is favored (only 13.8 % of the data are between −10 and −5 °C, where column-like growth dominates). We assume dendrite shapes for the entire dataset for two reasons. The first reason is that Maherndl et al. (2024) found that assuming plates or dendrites gives the same results within uncertainty estimates, and the second reason is that we want to keep the analysis of IMPACTS and HALO-(AC)³ data as consistent as possible.

The in situ method uses in situ measurements of ice particle area A, perimeter P, and D_max to derive M for individual ice particles, from which an average M for the particle population is derived. The in situ method is applied to 2D-S and HVPS-3 data for IMPACTS as was done with CIP and PIP data for HALO-(AC)³ in Maherndl et al. (2024). P and A in the unit of pixel and are used to calculate complexity $\mathit{\chi }=\frac{P}{\mathrm{2}\sqrt{\mathit{\pi }A}}$. Simulated rimed aggregates from Maherndl et al. (2023b) are used to derive empirical functions relating χ and D_max to M, where χ and D_max are derived using the same processing steps as for the respective cloud probes. Because these processing steps were slightly different for 2D-S and HVPS-3 operated during IMPACTS² from those for CIP and PIP during HALO-(AC)³, new fit functions (based on 18 352 simulated dendrites, with R²=0.92) had to be derived for IMPACTS:

$$\begin{array}{}\text{(3)}& {\log }_{\mathrm{10}}\left(M\right)={\displaystyle \frac{\mathrm{1.11}-\mathit{\chi }+\mathrm{0.00141}\cdot D_{\text{max}}}{\mathrm{0.00432}\cdot D_{\text{max}}+\mathrm{0.218}}}.\end{array}$$

Only a subset of ice particles can be used to derive M with the in situ method because particles cannot touch edges to derive P and must be large enough to derive meaningful χ. Because of these two criteria, ice particles with D_max in the range of about 1.0–1.4 and 2.0–6.0 mm are neglected by the in situ method when using the HALO-(AC)³ and IMPACTS particle probes, respectively. Therefore, we assume that the combined method – which uses the full PSD – gives more reliable results if the aircraft are reasonably colocated, as shown in Maherndl et al. (2024) for HALO-(AC)³. We use M derived with the combined method for all further analysis steps. For reference and uncertainty estimation, we show the in situ method M results in Sect. 4.1.1 and 4.1.2 and in Appendix A.

3.2 Deriving ice water content (IWC)

IWC is calculated by summing the product of ice particle mass m(D_max) and N(D_max) for the lower to upper size ranges of the probes, D_lower to D_upper:

$$\begin{array}{}\text{(4)}& \text{IWC}=\sum _{D_{\text{lower}}}^{D_{\text{upper}}}m\left(D_{\text{max}}\right)N\left(D_{\text{max}}\right)\mathrm{\Delta }{D}_{\text{max}},\end{array}$$

where ΔD_max is the size bin width. Here, m(D_max) is approximated by a power law relation with prefactor a_m and exponent b_m:

$$\begin{array}{}\text{(5)}& m\left(D_{\text{max}}\right)=a_m{D}_{\text{max}}^{b_m}.\end{array}$$

Here, a_m scales the density of ice particles (independent of particle size), while b_m modulates the size dependence of particle mass, which is related to particle shape and growth processes. In addition, a_m and b_m depend strongly on riming (e.g., Mitchell, 1996), and reported values in the literature range from 0.0058 to 466 for a_m and 1.8 to 3.0 for b_m in SI units (e.g., discussed by Mason et al., 2018). As shown by Maherndl et al. (2023a), a_m and b_m strongly depend on the amount of riming, which increases particle densities. Maherndl et al. (2023a) provide a_m and b_m values for discrete M, which are interpolated in this study to obtain parameters for a continuous M. We derive a_m and b_m for each time step as a function of the retrieved M. IWC is then calculated using Eq. (4) for each time step based on the measured PSD and the derived a_m and b_m parameters. We refer to this quantity as IWC_r (IWC accounting for riming).

To estimate the contribution of the riming process to IWC, we also calculate IWC using fixed mass–size parameters a_m and b_m for unrimed particles (also taken from Maherndl et al., 2023a), thereby neglecting density changes (e.g., due to riming). We call this quantity IWC_u. IWC_u can be seen as the “theoretical” IWC where the ice particles were unrimed, meaning that the riming contribution can be estimated from the difference between IWC and IWC_u. However, this implies that riming does not affect the size of the unrimed ice particle, which is not necessarily the case in nature. Riming typically leads to an increase in not only ice particle density but also ice particle size (Seifert et al., 2019). Therefore, we likely underestimate the contribution of riming to particle mass when comparing IWC_u to IWC. Since we are interested in the contribution of riming to IWC variability, this approach likely results in a conservative estimate of the contribution of riming to IWC variability.

3.3 Characterizing scales of IWC variability in clouds

Similar to Deng et al. (2024), we use the pair correlation function (PCF) to quantify the spatial inhomogeneity of ice water in the observed clouds. In discrete systems, the PCF describes the degree of deviation from the homogeneous Poisson process. In clouds, the PCF can be used to quantify the degree of clustering or variability of a certain parameter such as the number concentration of liquid droplets, the number concentration of ice particles, LWC, or IWC (e.g., Shaw et al., 2002; Saw et al., 2012a; Deng et al., 2024). The PCF applied to a one-dimensional parameter p is given by

$$\begin{array}{}\text{(6)}& \mathit{\eta }\left(r\right)={\displaystyle \frac{\stackrel{\mathrm{‾}}{p\left(\mathrm{0}\right)p\left(r\right)}}{(\stackrel{\mathrm{‾}}{p}{)}^{\mathrm{2}}}}-\mathrm{1},\end{array}$$

where p(0) is the parameter at a given point, p(r) is the parameter at the lag r from that point, and $\stackrel{\mathrm{‾}}{p}$ is the average of p (Kostinski and Jameson, 2000; Shaw et al., 2002). Thus, η(r) is a measure of the probability of finding clusters of p as a function of lag r compared to $\stackrel{\mathrm{‾}}{p}$. Positive values indicate the presence of clusters and the higher η(r) is, the higher the probability of finding clusters at that scale will be. If p follows a homogeneous Poisson distribution, which PCF assumes to be statistically homogeneous, then η(r)=0. Negative values indicate that the probability of finding clusters at that scale is lower than on average for the whole segment.

In this study, only straight flight segments with a minimum of 200 s of continuous in-cloud measurements are used to calculate η(r). The respective radar sensitivity limits are used to define “in cloud”. We allow measurement gaps with a maximum length of 5 s, which are linearly interpolated. Table 2 gives an overview of all segments we analyze, including duration and data amount. Because IWC is derived using running averages of 10 and 30 s for IMPACTS and HALO-(AC)³ data, respectively, we investigated the impact of the window size of the moving average on η(r). We found that increasing the window size from 1 to 10 (30) s for IMPACTS (HALO-(AC)³) decreases the absolute value of η(r). However, the lags r at which r η(r) is positive do not change (not shown). This is because applying a moving average smooths peaks in the 1 Hz signal but does not necessarily change their periodicity as long as the window size is reasonably small.

Table 2 Overview of analyzed segments including campaign, flight day, start and end times in UTC, and number of 1 s data points.

Additionally, we use power spectra in order to gain insight into scales of variability of CTH and LWP during HALO-(AC)³. To do this, each data segment is mean centered and linearly detrended. A Hann window is applied to each segment to minimize edge effects. Frequency is converted to wavelength using the aircraft speed v_air. With a minimum time range of 200 s per segment, we capture spatial scales of 12 km for HALO-(AC)³, meaning that we do not capture synoptic-scale motions. We interpret results up to 0.1 Hz, i.e., spatial scales of 600 m.

Figure 2 visualizes the PCF and power spectra for synthetic data. For a homogeneous Poisson process (Fig. 2a), η(r)=0 (Fig. 2d), and the power spectral density shows no significant peaks (Fig. 2g). For a periodic sine function with Poisson noise added (Fig. 2b), η(r) is positive for small lags and oscillates around 0 for larger lags with peaks occurring at multiples of the wavelength λ of the sine function (Fig. 2e). The power spectrum shows a peak at λ (Fig. 2h). When the modulus function is applied to the sine curve (Fig. 2c), η(r) (Fig. 2f) is smaller than in Fig. 2e due to the lower signal-to-noise ratio, and the oscillation occurs at $\mathit{\lambda }/\mathrm{2}$. The power spectrum also shows a peak at $\mathit{\lambda }/\mathrm{2}$ (Fig. 2i).

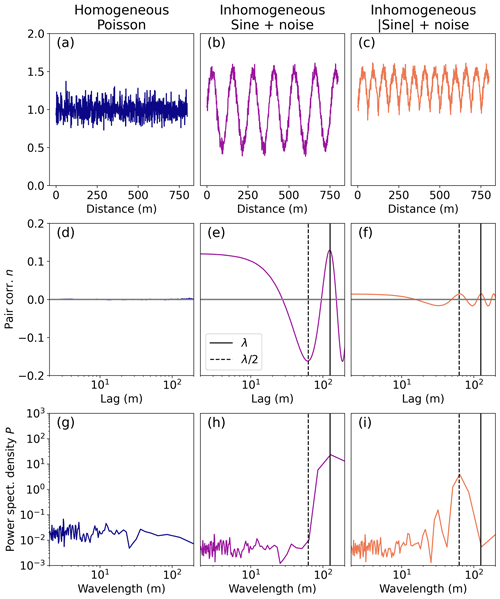
Figure 2 Schematic diagram introducing the pair correlation function (PCF) and power spectral density for (a) a homogeneous Poisson distribution signal, (b) a sine curve with wavelength λ and Poisson noise added, and (c) the same sine curve but mirrored upwards along x=1 to show the impact of λ and signal-to-noise ratio. The respective PCF η as a function of lag is shown in (d)–(f), while the power spectra density as a function of wavelength is shown in (g)–(i). The solid and dashed lines indicate λ and $\mathit{\lambda }/\mathrm{2}$ of the sine curve in (b), respectively.

4 Results and discussion

To characterize the influence of riming on the spatial variability of ice clusters in clouds, we first need to know the amount of riming and its impact on IWC. Second, we need to know spatial IWC cluster scales with and without riming. Therefore, this section is structured as follows. First, we quantify the amount of riming observed during the both campaigns (Sect. 4.1). We then show that the retrieved amounts of riming have a significant impact on IWC (Sect. 4.2). Finally, we quantify in-cloud IWC variability (Sect. 4.3) and discuss the impact of riming on spatial scales and the probability of IWC clustering in clouds.

4.1 Riming occurrence

MPC properties, synoptic situations (Sect. 2.3), and measurement locations (Fig. 1) vary between IMPACTS and HALO-(AC)³. Clouds during colocated IMPACTS segments have much larger vertical extents than during HALO-(AC)³ segments. The median CTH during IMPACTS segments is 7.3 km (25 %–75 % quantile range: 6.3–7.8 km). Here, we define CTH as the height of the highest radar range gate with continuous Z_e above the in situ aircraft altitude.

Clouds observed during colocated HALO-(AC)³ segments were predominately shallow roll clouds that formed during MCAOs. The maximum CTH during all segments was 2.2 km (25 %–75 % percentile range: 0.69–1.1 km). Cloud properties during 1 and 4 April 2022 are described in detail in Schirmacher et al. (2024).

In the following, we give a brief overview of the differences in MPCs between the two campaigns using two typical example cases. We show a flight segment from 5 February 2020 for IMPACTS (Sect. 4.1.1) and from 1 April 2022 for HALO-(AC)³ (Sect. 4.1.2). We present M retrieved with combined and in situ methods and discuss uncertainties. We then extend this to data from all colocated segments (Sect. 4.1.3).

4.1.1 Case study 1: mid-latitude winter storm on 5 February 2020

Figure 3 shows a 64 km segment from 5 February, where ER-2 and P-3 sampled a developing low-pressure system over Illinois from 23:07:26 to 23:12:40 UTC. According to the level-2 Moderate-resolution Imaging Spectroradiometer (MODIS) cloud product (NASA Worldview, 2024), the cloud top temperature (CTT) was −33 ± 5 °C. W-band Z_e shows the deep cloud with convective-cell structures near cloud top from which sheared fall streaks extend downward (Fig. 3a). P-3 measured the number of ice particles larger than 50 µm N_i in the range of 910 to 2800 m³ (Fig. 3b). Here we show D₃₂ (Fig. 3b), which is the proxy for the mean mass-weighted diameter (e.g., Maahn et al., 2015). D₃₂ is defined as the ratio of the third to the second measured PSD moments (e.g., Mitchell, 1996). During the first 20 km of the segment, ice particles had D₃₂ of about 3 mm and were lightly rimed with M of about 0.02 (Fig. 3c). Following this, D₃₂ increases up to 8 mm, indicating aggregates, and M drops below the riming threshold of 0.01. From −88.9° E onward, D₃₂ decreases and M increases. Combined-method M results using the different frequencies show good agreement between X, Ku, and Ka band. W-band results are likely biased high due to the high D₃₂, as will be discussed in Sect. 4.1.3. IWC is calculated with Eq. (4) using (1) the measured PSD and mass–size parameters a_m and b_m for unrimed particles (blue line) and (2) a_m and b_m based on lookup tables (Maherndl et al., 2023a) for each time step depending on the retrieved M for each frequency (black lines). The derived IWC from Ku-band M varies between 0.015 and 0.31 gm⁻³ (Fig. 3d). If riming is neglected, i.e., mass–size parameters for unrimed particles are used in the IWC calculation, IWC is on average lower by a factor of 3.7.

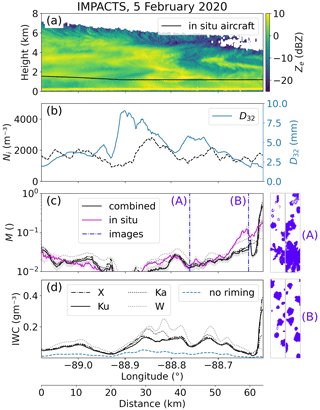
Figure 3 Colocated flight segment from 23:07:26 to 23:12.40 UTC on 5 February 2020 during IMPACTS. (a) W-band radar reflectivity Z_e and P-3 flight altitude; (b) ice number concentration N_i and mass-weighted diameter D₃₂ derived from the 10 s running averaged particle size distribution (PSD); (c) normalized rime mass M from the combined (black) and in situ (magenta) methods, including uncertainty estimates (combined: optimal estimation (OE) standard deviation; in situ: 10 s running standard deviation), where the combined method was applied to X-, Ku-, Ka-, and W-band Z_e (Ku-band results, which are used in the further analysis, are shown as solid lines); (d) ice water content (IWC) derived from the 10 s running averaged PSD, combined method M (black), and assuming M=0 (blue). Combined method results for different radar frequencies are drawn as dashed lines. The 2-DS images for (A) −88.78° E and (B) −88.69° E are shown in blue next to panels (c) and (d).

The increase in M starting at −88.7° E could be related to the decrease in CTH (as seen by the radar). Some particles are possibly rimed in liquid layers near cloud top and fall down to the measurement location. On their way down, they may undergo additional growth processes (condensational growth or aggregation), leading to a decrease in M, since M is normalized to particle size. However, King probe measurements show that liquid water also occurs at the P-3 position. Therefore, additional riming may occur at the P-3 location and possibly in cloud layers above. The 2-DS images (Fig. 3) show a change from large, lightly rimed aggregates to small, more heavily rimed particles.

4.1.2 Case study 2: Arctic roll clouds on 1 April 2022

Figure 4 shows a 35 km segment from 1 April, where Polar 5 and Polar 6 sampled perpendicular to the roll cloud structures formed during MCAO conditions over the Fram Strait from 11:20:38 to 11:33:02 UTC (see Maherndl et al., 2024, for a detailed discussion of the case and particle images). The MODIS CTT was −18 ± 5 °C. W-band Z_e shows the vertical structure of the individual cloud rolls (Fig. 4a). While Polar 6 was flying close to cloud top, N_i was high with a maximum of 27 300 m⁻³, and D₃₂ was low with a minimum of 0.077 mm (Fig. 4b). As Polar 6 descended, N_i dropped to a minimum of 4600 m³, while D₃₂ increased up to 1.4 mm (Fig. 4b). M oscillates between 0.01 and 0.1, with peaks occurring in streaks of high Z_e (Fig. 4c). The resulting IWC is between 0.022 and 0.084 g m⁻³. This is a factor of 2.8 higher than using a mass–size parameterization for unrimed particles (Fig. 4d).

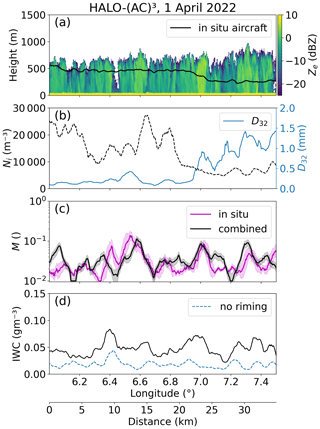
Figure 4 The same as Fig. 3 but for the colocated flight segment from 11:20:38–11:33:02 UTC on 1 April 2022 during HALO-(AC)³. Only W-band radar reflectivities are available.

Both methods used to derive M agree well for this segment in terms of M distributions and location and extent of maxima (R²=0.52). Statistical agreement between the two methods was achieved for all HALO-(AC)³ segments used in this study. However, spatiotemporal agreement could not be achieved for inhomogeneous cloud observations (e.g., when Polar 6 was flying in and out of cloud near the CTH), as discussed in Maherndl et al. (2024).

4.1.3 Riming product statistics and discussion

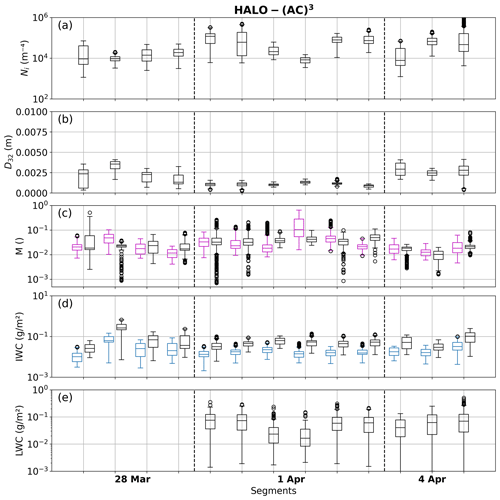
In the previous section, two case studies were used to show differences between clouds observed during the two campaigns, especially in terms of vertical extent, structure, and riming. Despite these differences, normalized rime mass M distributions derived for IMPACTS and HALO-(AC)³ are similar (Fig. 5a and b). Median M values for all colocated IMPACTS segments are 0.024, 0.022, 0.025, and 0.034 when derived with X-, Ku-, Ka-, and W-band Z_e, respectively. During colocated HALO-(AC)³ segments, median M is 0.024. For IMPACTS, the discrepancy between the W-band results and the other frequency bands is due to the occurrence of large ice particle sizes. Because of saturation effects, the riming-dependent parameterization (Maherndl et al., 2023a) has a positive Z_e bias for large relative sizes of scattering particles. The relative size of a scattering particle is defined by its size parameter $x=\mathrm{2}\mathit{\pi }{\mathit{\alpha }}_{\mathrm{e}}{D}_{\text{max}}/\mathit{\lambda }$, where α_e is the effective aspect ratio of the ice particle, and λ the radar wavelength. Positive biases occur for x>4. The positive Z_e bias for x>4 results in a positive bias of M. For IMPACTS, 25 % of the data have D₃₂>3.2 mm, which corresponds to x=4 at 94 GHz assuming a typical value of α_e=0.6. Therefore, W-band results for IMPACTS are not as trustworthy as the other wavelengths and are not used in the following analysis. Unlike IMPACTS, the M bias is negligible for HALO-(AC)³ due to the smaller particle sizes, and D₃₂<3.2 holds for 90 % of the data. Appendix A gives an overview of microphysical parameters during each analyzed segment.

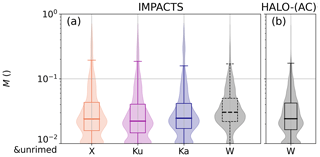
Figure 5 Boxplots and superimposed violin plots showing normalized rime mass M results obtained from a closure of colocated radar reflectivity Z_e and in situ particle size distribution (“combined method” from Maherndl et al., 2024) for radar reflectivities available during (a) IMPACTS and (b) HALO-(AC)³. W-band results during IMPACTS are dashed due to biases (see text). M<0.01 is plotted at 0.01 to be visible on the logarithmic scale.

4.2 Sensitivity study

To show the effect of expected M on Z_e and to evaluate whether the retrieved amounts of riming significantly impact IWC, we conduct a sensitivity study.

We assume that N(D_max) follows a modified gamma distribution and use the normalized form introduced by Delanoë et al. (2005, 2014) and extended by Maahn et al. (2015) for the maximum dimension D_max:

$$\begin{array}{}\text{(7)}& {\displaystyle }\begin{array}{rl}{\displaystyle }N\left(D_{\text{max}}\right)=& {\displaystyle }{N}_{\mathrm{0}}^{\ast }{\displaystyle \frac{(b_m+\mathit{\mu }+\mathrm{1}{)}^{b_m+\mathit{\mu }+\mathrm{1}}\mathrm{\Gamma }(b_m+\mathrm{1})}{\mathrm{\Gamma }(b_m+\mathit{\mu }+\mathrm{1})(b_m+\mathrm{1}{)}^{(b_m+\mathrm{1})}}}\\ {\displaystyle }& {\displaystyle }\times {\left({\displaystyle \frac{D_{\text{max}}}{D_m}}\right)}^{\mathit{\mu }}{e}^{-(b_m+\mathit{\mu }+\mathrm{1})D_{\text{max}}/D_m},\end{array}\end{array}$$

where $N_{\mathrm{0}}^{\ast }$ is the overall scaling parameter, μ is the shape parameter, and D_m is the “mass-weighted” scaling parameter for the particle size. We vary $N_{\mathrm{0}}^{\ast }$ and D_m – which can be calculated from PSD moments (see Maahn et al., 2015) – based on 10 % to 90 % quantile values derived from all measured PSDs during IMPACTS. Only IMPACTS data were chosen because larger particles and higher number concentrations were measured during IMPACTS than during HALO-(AC)³. Here, μ is varied from 0 to 64 based on extreme values reported in the literature (Tridon et al., 2022). M is varied from 0.005 to 1, corresponding to the 10 % quantile of M retrieval results from both campaigns and the maximum “physical” M based on its definition.

We find that although the median M is below 0.03 for both campaigns, even small amounts of riming – or rather changes in ice particle density – can result in large changes in IWC. Figure 6 shows IWC calculations assuming gamma PSDs with varying $N_{\mathrm{0}}^{\ast }$ (left column) and M (right column) as a function of D_m. Similar to Maahn and Löhnert (2017), we find that the shape parameter μ does not significantly impact IWC or Z_e, and therefore only μ=0 is shown. D_m, which can be seen as a proxy for particle size, has the largest effect on IWC. Changing D_m from 1 to 8 mm changes IWC by 3 orders of magnitude. IWC increases by about 1 order of magnitude, when $N_{\mathrm{0}}^{\ast }$ – the proxy for the total number concentration of particles – is increased by 1 order of magnitude. Depending on D_m, varying M can result in IWC changes of up to 2 orders of magnitude. Considering only M values encountered during the campaigns analyzed, the change in IWC reaches 1 order of magnitude.

In order to show the effect of riming on radar reflectivity Z_e, which can be considered a proxy for IWC, we conduct a sensitivity study for Ku- and Ka-band Z_e. The aim is to highlight the importance of accounting for riming in radar retrievals. Z_e is forward simulated using the same PSDs with PAMTRA assuming a temperature of −10 °C. Particle scattering is parameterized with the riming-dependent parameterization (Maherndl et al., 2023a). X band is not shown due to being nearly identical to Ku band;, and W band is not shown due to the riming-dependent parameterization bias for large D_m at W band (see Sect. 4.1.3). Varying M within the observed ranges results in Z_e changes of up to 20 dB depending on D_m for both Ku and Ka band, albeit with a slightly larger spread at Ka band. Similar to Fig. 6, varying D_m results in the largest Z_e changes. Observed ranges of M result in larger Z_e changes than observed ranges of $N_{\mathrm{0}}^{\ast }$. Thus, in our dataset Z_e depends more on riming than on number concentration.

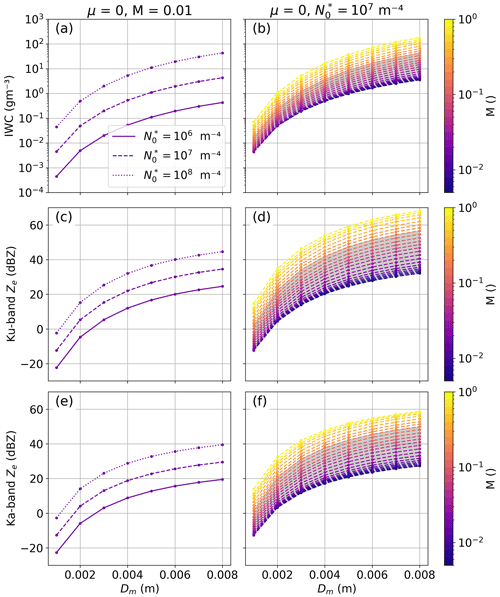
Figure 6 Ice water content (IWC) (a, b), Ku-band Z_e (c, d), and Ka-band Z_e (e, f) calculated from gamma particle size distributions as functions of D_m parameter. Results for varying $N_{\mathrm{0}}^{\ast }$ parameters are shown as solid and dashed lines in (a), (c), and (e), while results for varying normalized rime mass M are shown with different colors in (b), (d), and (f). Shaded areas in (b), (d), and (f) indicate M ranges observed during IMPACTS (90 % range: $\mathrm{0.005}<M<\mathrm{0.15}$).

We therefore conclude that the effect of riming on IWC should not be neglected for the range of M observed during HALO-(AC)³ and IMPACTS to avoid biases of up to 1 order of magnitude in IWC.

4.3 Quantifying in-cloud IWC variability with and without riming

Because even small amounts of riming have a significant effect on IWC, in the following we evaluate the differences in IWC variability when riming is considered versus when riming is neglected. As described in Sect. 3.2, IWC is calculated with Eq. (4) based on the measured PSD and (1) using mass–size parameters a_m and b_m for unrimed particles (IWC_u) and (2) varying a_m and b_m for each time step as a function of the retrieved M (IWC_r). During all analyzed IMPACTS flight segments, the rime mass (IWC_r−IWC_u) makes up 68.6 %, 65.7 %, and 68.8 % of IWC_r based on X-, Ku-, and Ka-band results, respectively. During HALO-(AC)³, the rime mass makes up 62.7 %.

Figure 7 shows the average PCF η over all analyzed IMPACTS and HALO-(AC)³ segments for N_i (Fig. 7, first column), IWC_r, and IWC_u (Fig. 7, second column). To visualize the difference between IWC_r and IWC_u, the third column of Fig. 7 shows ${\mathit{\eta }}_{{\text{IWC}}_{\mathrm{r}}}-{\mathit{\eta }}_{{\text{IWC}}_{\mathrm{u}}}$. This allows us to isolate the contribution of the riming process to IWC. Positive values of ${\mathit{\eta }}_{{\text{IWC}}_{\mathrm{r}}}-{\mathit{\eta }}_{{\text{IWC}}_{\mathrm{u}}}$ indicate that riming increases the variability of IWC clusters at the given lag, while negative values are related to riming smoothing out IWC variability. Because we are interested in the spatial scales at which riming influences IWC variability, we only discuss the differences greater than zero.

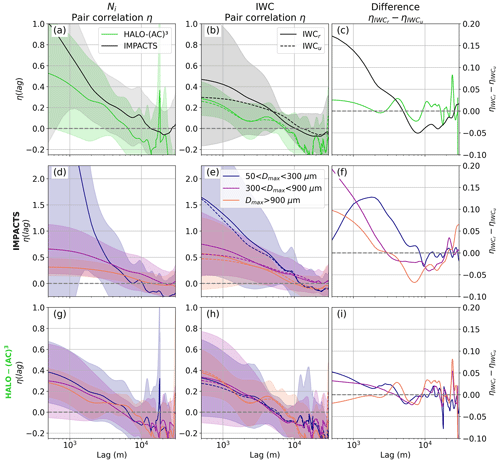
Figure 7 Average pair correlation function (PCF) η as a function of lag calculated for (a) ice number concentration N_i and (b) ice water content (IWC) during IMPACTS (black) and HALO-(AC)³ (green) segments. IWC is calculated with (solid line) and without (dashed line) accounting for riming, and differences are plotted in (c). Shaded areas show standard deviations. In (d)–(i), the particle size distributions are split into small ($\mathrm{50}<D_{\text{max}}<\mathrm{300}$ µm), medium ($\mathrm{300}<D_{\text{max}}<\mathrm{900}$ µm), and large (D_max>900 µm) particle sizes. Panels (d)–(f) and (g)–(i) are as in panels (a)–(c) but show the size dependency of η during IMPACTS and HALO-(AC)³, respectively. Note the different scales on the y axes.

For both N_i and IWC, IMPACTS segments have higher η on average than HALO-(AC)³ segments, implying that N_i and IWC have more variability on the spatial scales examined (Fig. 7a and b). Note that both quantities are calculated from running PSD averages of 10 and 30 s for IMPACTS and HALO-(AC)³, respectively, to cover similar spatial scales (about 1.8 km) given the different flight speeds. The smaller number of data points averaged for IMPACTS could lead to higher variability. However, computing η for 30 s running averages results in similar curves with nearly the same lags, where η=0, and slightly lower η, but this value is still higher than for HALO-(AC)³ (not shown).

During IMPACTS, variability occurred at larger spatial scales than during HALO-(AC)³, as indicated by positive η at larger lags (Fig. 7a and b). Differences between η for N_i and IWC indicate that ice growth processes play a large role in IWC variability in addition to ice formation processes. For both campaigns, η>0 for IWC is shifted to larger spatial scales than for N_i, indicating that ice growth processes lead to increased variability at large spatial scales. For IMPACTS, accounting for riming shifts the scales of IWC variability to slightly smaller lags and increases η significantly at small lags, meaning that riming increases IWC variability at lags <5 km (Fig. 7c). For HALO-(AC)³, riming leads to IWC variability at lags below 1 km and between 3–5 km. (Fig. 7c) However, the differences between ${\mathit{\eta }}_{{\text{IWC}}_{\mathrm{r}}}$ and ${\mathit{\eta }}_{{\text{IWC}}_{\mathrm{u}}}$ are smaller than for IMPACTS.

4.3.1 Dependency on particle size

To identify which particle size range contributes most to the N_i and IWC variability, we split the PSD into small ($\mathrm{50}<D_{\text{max}}<\mathrm{300}$ µm), medium ($\mathrm{300}<D_{\text{max}}<\mathrm{900}$ µm), and large (D_max>900 µm) particle sizes to calculate N_i and IWC (Fig. 7d–i). For IMPACTS, the probability of small-particle N_i (IWC) clusters is higher than for medium and large particles below 3.5 km (10 km). During HALO-(AC)³, η is similar regardless of size. However, positive η_IWC values – indicating the occurrence of IWC clusters – are shifted to slightly larger lags for large particles (9 km as opposed to 5–6 km for small and medium sizes).

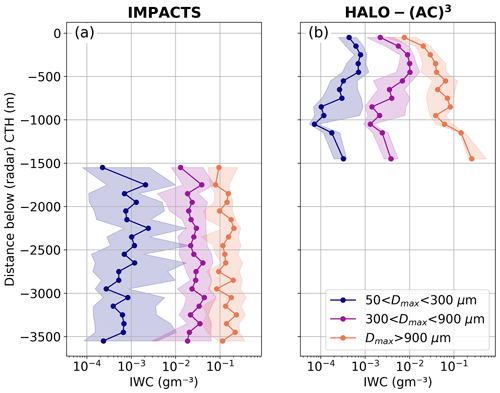
The in-cloud measurement location could influence the dependence of N_i and IWC variability on particle size due to size sorting, i.e., more small particles near the CTH and larger particles at lower heights. During the analyzed HALO-(AC)³ segments, clouds were shallow, and Polar 6 measurements took place on average 440 m below the CTH (as measured by W-band radar). During IMPACTS, much deeper cloud systems were observed, and P-3 on average sampled at larger vertical distances from the cloud top (3.3 km) than during HALO-(AC)³. W-band radar reflectivity Z_e – which can be seen as a proxy for IWC – shows higher variability near CTH for both IMPACTS and HALO-(AC)³ clouds (Fig. 8). Similar to Fig. 7, we use PCF to characterize the variability of Z_e in linear units. For each IMPACTS (HALO-(AC)³) flight segment, η is calculated for Z_e cross sections in 100 m (50 m) steps from the average CTH downward. In general, Z_e variability is larger near CTH at lags below 5 and 2 km for IMPACTS and HALO-(AC)³, respectively. The higher variability is likely linked to cloud top generating cells, as seen in case study 1 (Fig. 3a). Generating cells contain more liquid and ice and have stronger updrafts than adjacent cloud regions. HALO-(AC)³ clouds show less variability and are homogeneous at smaller spatial scales (η=0 is at smaller lags) than clouds during IMPACTS. Size sorting may play a larger role in IMPACTS due to the larger cloud depths compared to the shallow MCAO clouds during HALO-(AC)³. However, the N_i and IWC distributions as functions of distance to CTH indicate the opposite (Appendix B). Nevertheless, N_i and IWC derived for small particles only show much more variability as a function of the distance to CTH for IMPACTS (Appendix B).

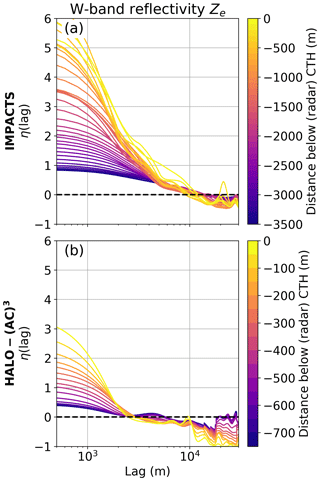
Figure 8 Average pair correlation function (PCF) η as a function of lag calculated for horizontal cross section of W-band Z_e (in linear units) during (a) IMPACTS and (b) HALO-(AC)³ flight segments. Cross sections are taken in 100 and 50 m steps from the average cloud top height (CTH) of each segment downward for IMPACTS and HALO-(AC)³ data, respectively. Note the different color bar scales.

The higher variability of small particle counts during IMPACTS is therefore likely due to higher numbers of ice-nucleating particles (INPs) available at mid-latitudes (Petters and Wright, 2015). During the analyzed HALO-(AC)³ flight days, INP concentrations collected with filters on board Polar 6 were very low, often below the detection threshold (Wendisch et al., 2024). No INP measurements were conducted during IMPACTS, and therefore a direct comparison cannot be made. Another explanation could be that there is more secondary ice production (SIP) occurring during IMPACTS than during HALO-(AC)³.

Differences between η computed for IWC_r and IWC_u using the different size bins (Fig. 7f) show that riming increases the probability of IWC clusters for lags smaller than 9 km for small particles during IMPACTS. For medium and large particles, riming increases the probability of IWC clusters at lags smaller than 3 km. For medium and large particles, the enhancement increases as the lag decreases, while for small particles the maximum enhancement occurs at a lag of about 2 km. An enhancement for small particles may indicate SIP associated with riming, such as rime splintering. During HALO-(AC)³ (Fig. 7i), riming enhances the probability of IWC clusters for lags smaller than 4 km for small and medium particles, and the enhancement is generally larger the smaller the lag. For large particles, only lags of about 3–5 km lead to an increase in IWC variability.

4.3.2 Dependency on riming

To understand which spatial scales dominate the riming-driven IWC variability, we perform a Monte Carlo random test for specific sampling distances following Deng et al. (2024). This approach allows us first to handle the flight segments of different lengths in a statistically robust manner and second to analyze the dependence on flight segment distance. For each flight segment, we randomly select a sub-segment with a distance of d km, where we vary d in 1 km steps from 1 to 15 km. We then calculate η for that segment. This is repeated 100 times, and the average η over all (sub)segments of the respective campaign is calculated. In principle, parts of sub-segments can be resampled. However, the sampling process is random. To perform the averaging, we divide η into 200 and 60 m bins for IMPACTS and HALO-(AC)³, respectively, corresponding to the respective distances covered in 1 s for the respective typical flight speeds. The results are shown in Fig. 9, where the average η for N_i, IWC_r, and IWC_u are plotted as a function of distance d and lag. Curves (shaded) where η=0 are included to show the maximum spatial scales at which ice clusters are likely to occur, given a sampling distance d.

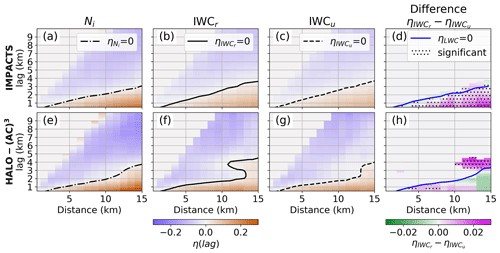
Figure 9 Average pair correlation function (PCF) η as a function of distance and lag calculated using all (a–c) IMPACTS and (e–g) HALO-(AC)³ flight segments for (a, e) N_i, (b, f) ice water content (IWC) accounting for riming IWC_r, and (c, g) IWC assuming no riming IWC_u. The difference between (b) and (c) is shown in (d). The difference between (f) and (g) is shown in (h). Differences in (d) and (h) are only shown where ${\mathit{\eta }}_{{\text{IWC}}_{\mathrm{r}}}>\mathrm{0}$. Areas where differences are significant according to a Student's t test (95 % significance threshold) are hatched. Here, η=0 is drawn as shaded lines for the ice number concentration N_i (dashed–dotted black), IWC_r (solid black), IWC_u (dashed black), and liquid water content (LWC, solid blue), where LWC measurements from King probe (Nevzorov probe) measurements obtained during IMPACTS (HALO-(AC)³) are used.

During IMPACTS, the maximum N_i cluster spatial scale in clouds increases from 0.6 to 3.1 km at distances d of 2 to 15 km (Fig. 9a). LWC cluster scales measured by the King probe behave similarly to N_i (not shown), and the maximum cluster scales increase from 0.6 to 3.0 km. This suggests simultaneous liquid and ice formation in regions of high supersaturation with respect to ice. Maximum IWC cluster scales (whether or not riming is considered) increase from 0.6 to 3.6 km (Fig. 9b and c). At distances less than 6 km, N_i and IWC have roughly the same cluster scales; at distances greater than 10 km, IWC clusters occur at larger spatial scales. Differences between positive values of IWC_r and IWC_u (Fig. 9d) reveal that riming enhances the probability of ice clusters for distances greater than 6 km for lags from about 1 to 10 km (at distances of 12 km). To show the statistical significance of this enhancement, a one-sided Student's t test with a significance threshold of 95 % is used. Areas where differences are significant are hatched (Fig. 9d). The enhancement occurs at similar spatial scales as for LWC clusters, suggesting that riming is driven by LWC variability.

During HALO-(AC)³, the maximum N_i cluster spatial scale in clouds increases from 0.5 to 3.7 km at distances of 2 to 15 km (Fig. 9e). Similar to IMPACTS data, LWC clusters measured by the Nevzorov probe behave similarly to N_i clusters, increasing from 0.5 to 3.3 km, but they have slightly smaller spatial scales. Maximum IWC cluster scales, assuming no riming, increase from 0.6 to 3.8 km and thus occur at about the same spatial scales as N_i clusters (Fig. 9g). Accounting for riming, the maximum IWC cluster scales show a distinct behavior for distances larger than 10 km: η increases at 3–5 km, indicating that riming increases variability at these scales (Fig. 9f), which cannot be explained by the LWC variability. Statistically significant differences between positive IWC_r and IWC_u (Fig. 9h) further highlight this feature.

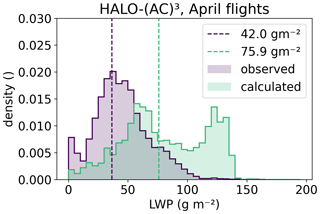
To explain the different spatial scales at which riming increases IWC variability, we look at lidar-derived CTH. In previous sections, we derived CTH from radar measurements to make IMPACTS and HALO-(AC)³ comparable. For HALO-(AC)³, a more sophisticated CTH product based on lidar – which is more sensitive to liquid layers at cloud top than the radar – is available and is used below. The lidar detects small liquid droplets at cloud top, which follow vertical motions, therefore leading to higher CTH in updraft regions (Abel et al., 2017). When computing the average power spectrum of CTH observed during the flight days studied, distinct peaks at wavelengths of 750 m and 1.2 km occur for all days. These wavelengths correspond to the typical roll cloud and circulation wavelengths as derived by Schirmacher et al. (2024) (Fig. 10a, d, g). At these wavelengths, peaks in LWP also occur for all days (Fig. 10b, e, and h), further indicating enhanced formation and growth of liquid droplets in the updraft regions of the convectional cell cloud structures. On 28 March, a prominent peak in the CTH spectrum at 3–5 km indicates additional mesoscale updraft features (Fig. 10a). However, the LWP spectrum shows only a weak peak around 5 km (Fig. 10b). On 1 April, both CTH and LWP power spectra have peaks at 3–5 km (Fig. 10d and e). On 4 April, there are no prominent peaks at wavelengths of 3–5 km (Fig. 10g and h). Given that the least (most) amount of riming (Fig. 10c, f, and i) occurred on 4 (1) April, we conclude that in the studied MCAO clouds, mesoscale updraft features likely enhance riming at spatial scales of 3–5 km. The enhancement could be due to prolonged lifetimes of ice crystals in clouds (28 March), increased amounts of liquid water, or both (1 April), and this leads to an increase in IWC amount and variability.

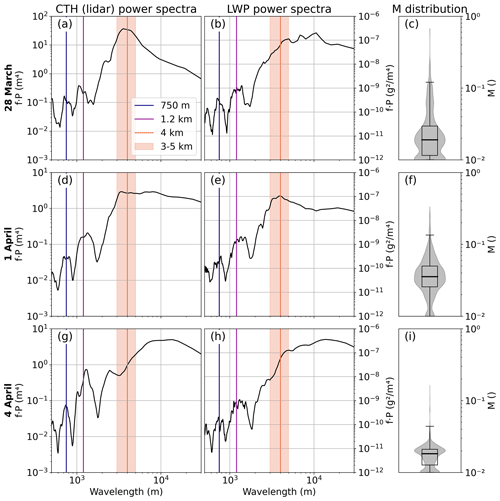
Figure 10 Power spectra of (a), (d), and (g) cloud top height (CTH) as derived from lidar and (b), (e), and (h) liquid water path (LWP) during colocated HALO-(AC)³ flight days. The wavelength has been calculated based on the aircraft flight speed. The blue and purple lines show the typical roll cloud and circulation wavelengths as derived by Schirmacher et al. (2024). The shaded orange area shows the 3–5 km range, where riming causes additional IWC clustering. Panels (c), (f), and (i) show the corresponding normalized rime mass M distributions.

4.4 A conceptual model of how riming impacts IWC clusters in MCAO roll clouds

The results discussed above help to better understand scales of in-cloud IWC clustering in different types of MPCs and link them to some of the microphysical processes involved. Although there are significant unknowns, the following summarizes our findings from the perspective of colocated remote sensing and in situ measurements.

In the analyzed segments of winter storm clouds measured during IMPACTS, IWC clusters occur at spatial scales smaller than about 3 km for segment distances of 15 km. Accounting for riming increases the probability of ice clusters (Fig. 9d). However, riming does not significantly increase the occurrences of IWC clusters at specific scales. LWC clusters for segment distances of 15 km occur at the same spatial scales of about 3 km as clusters of N_i. Therefore, liquid droplets and ice particles are likely to form together in regions of supersaturation with respect to liquid and ice. Since LWC clusters and the IWC cluster enhancement by riming occur at similar spatial scales, we hypothesize that LWC variability (at least in part) drives riming. By increasing IWC, riming leads to increased probabilities of IWC clusters for IMPACTS.

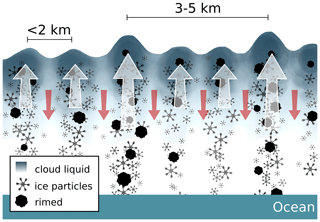
For HALO-(AC)³, Fig. 11 shows a sketch of the maximum spatial scales, where we found ice clusters to occur for MPCs observed during MCAOs. In these MCAO roll clouds, ice clusters occur on spatial scales of the roll cloud wavelengths. In the updraft regions of the convective cells, which occurred on average every 750 m and 1.2 km, liquid droplets and ice particles are formed. LWP and CTH are increased by vertical motions and condensational growth. Ice particles grow through depositional growth and riming, leading to enhanced probabilities of ice clusters at these scales. When an ice particle's mass has increased sufficiently, it may precipitate or sublimate below cloud. Aggregation can occur when ice particles collide. In the presence of additional mesoscale updraft features, IWC clusters also occur at spatial scales of 3–5 km (Fig. 9h). Due to the increased vertical motion, ice particles are suspended longer, have more time to rime, and can reach higher masses before precipitating. Increased LWP may enhance the amount of riming but is not a necessary criterion based on the cases analyzed. This hypothesis is supported by the fact that the observed LWP is not sufficient to explain the retrieved rime masses, assuming that particles continuously collect liquid water by falling through the liquid layer, as we show in Appendix C. The enhanced occurrence of riming drives the additional increase in IWC cluster probability on spatial scales of 3–5 km.

Figure 11 A conceptual diagram summarizing ice cluster spatial scales driven by riming as observed in MCAO roll clouds during HALO-(AC)³. For further explanation, see Sect. 4.4.

5 Conclusions

In this study, we use airborne measurements of mid-latitude and high-latitude mixed-phase clouds (MPCs) to investigate the spatial variability of ice clusters within clouds. We further investigate how this variability is linked to riming, which we quantify through the closure of colocated cloud radar reflectivity and in situ particle size distribution (PSD) measurements. The pair correlation function (PCF) is used to quantify the spatial scales of ice clusters and the variability of ice water content (IWC) when accounting for riming (IWC_r) and neglecting riming (IWC_u). The main findings are as follows.

1. Although the synoptic situations and the resulting cloud systems were vastly different during the two aircraft campaigns analyzed, the retrieved amounts of riming were similar. The median normalized rime mass M was 0.023 and 0.024 during IMPACTS (mid-latitude winter storms) and HALO-(AC)³ (Arctic MCAO roll clouds) segments, respectively (Fig. 5). Clouds were deep (shallow) during IMPACTS (HALO-(AC)³) segments, and in situ measurements were conducted at an average vertical distance of 3.3 km (440 m) from the cloud top.

2. The observed spread of M can increase IWC by up to 2 orders of magnitude, depending on the size of the particle population (Fig. 6). In sum, the rime mass makes up about 66 % and 63 % of the total IWC during the analyzed IMPACTS and HALO-(AC)³ flight segments, respectively. Therefore, riming has a similar impact on IWC to the observed spread of number concentration and should not be neglected when estimating IWC.

3. PCF revealed that N_i clusters occur with increased probability at spatial scales smaller than 10.5 and 6.5 km within clouds during IMPACTS and HALO-(AC)³, respectively. IWC clusters dominate for spatial scales of 10 and 7 km. For IMPACTS, small particles dominate N_i and IWC variability on small spatial scales, while for HALO-(AC)³ there is no particle size dependence (Fig. 7). This could be related to ice formation processes and the higher availability of INP at mid-latitudes. However, this hypothesis could not be confirmed with the available data.

4. During IMPACTS, the maximum spatial scales of N_i, IWC, and LWC clusters inside clouds are 0.6–3 km for distances of 2–15 km. During HALO-(AC)³, the maximum spatial scales of N_i, IWC, and LWC clusters are similar, with about 0.5 km for distances of 2 km and about 4 km for 15 km. However, for IWC during HALO-(AC)³, the probability of cluster occurrence is increased on scales of 3–5 km when segment distances are larger than 10 km (Fig. 9).

5. During IMPACTS, accounting for riming does not significantly change IWC cluster scales in clouds but increases the probability of clusters for segment distances larger than 6 km (Fig. 9d). This enhancement occurs at scales similar to LWC variability. More riming is likely to occur in regions of enhanced LWC, increasing IWC. Since clusters of IWC neglecting riming have similar spatial scales to N_i, LWC, and IWC accounting for riming, ice clustering is likely linked to ice formation processes in regions of high supersaturation with respect to liquid and ice.

6. In contrast, riming impacts IWC clustering in clouds at two distinct scales during HALO-(AC)³ (Fig. 9h). First, riming increases the probability of IWC clusters at spatial scales below 2 km, which corresponds to the wavelength of the roll cloud updraft features. N_i, IWC_r, IWC_u, and LWC all have similar spatial variability, indicating simultaneous ice and liquid formation and growth in these regions. Increased LWC again increases riming, which increases IWC. Second, riming leads to IWC clustering on spatial scales of 3–5 km, which cannot be explained by the typical roll cloud and roll circulation wavelengths. Power spectra of CTH show peaks at these spatial scales on the flight days with enhanced riming (Fig. 10). This suggests that the presence of mesoscale updraft features – which cause greater CTH through lifting of small particles near cloud top – leads to enhanced occurrence of riming and hence additional IWC clustering. Increased LWP may enhance the effect but is not a necessary criterion based on the cases analyzed. Theoretical analysis shows that updrafts are likely necessary to explain the observed riming values (Fig. C1).

These results help to improve our understanding of how riming is linked to in-cloud IWC variability and can be used to evaluate and constrain models' representations of MPCs. While we have shown that riming enhances in-cloud IWC variability and causes additional IWC clustering at large spatial scales of 3–5 km in Arctic MCAO clouds, further research is needed to link these results to surface precipitation. Future studies should investigate the link between riming-driven IWC variability and snowfall variability. In addition, profiles of vertical wind speed and turbulence are needed to better understand their importance for riming.

Appendix A: Microphysical overview of analyzed segments

Figure A1 (Fig. A2) presents an overview of microphysical parameters (N_i, D₃₂, M, IWC, LWC) observed during each analyzed IMPACTS (HALO-(AC)³) segment. Case study 1 (case study 2) is the fifth segment on 5 February (second segment on 1 April).

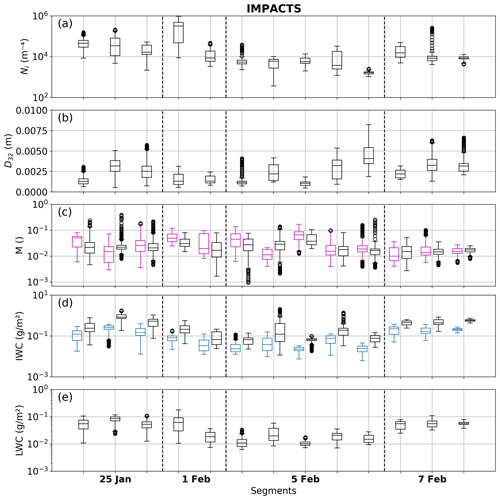
Figure A1 Boxplots of (a) ice number concentration N_i, (b) mass-weighted diameter D₃₂, (c) normalized rime mass M, (d) ice water content (IWC), and (e) liquid water content (LWC) derived during each IMPACTS segment. In (c) combined (Ku band) and in situ method results are shown in black and magenta, respectively. In (d) IWC is calculated when accounting for riming (using the combined method M; black) and neglecting riming (M=0, blue).

Figure A2 The same as Fig. A1 but for HALO-(AC)³ segments.

Appendix B: Vertical distribution of N_i and IWC

To investigate whether size sorting is the reason for the particle size dependence of N_i and IWC variability (Sect. 4.3.1), we show vertical distributions of N_i and IWC for the different size ranges in Figs. B1 and B2, respectively. Data during colocated segments are binned by their distance to CTH (as derived from radar measurements) in 100 m bins. Only bins with at least 100 data points are shown. This leaves no data for 1.5 km below cloud top during IMPACTS. While HALO-(AC)³ data show size sorting near the cloud top for both N_i and IWC, this is not the case for IMPACTS. However, size sorting could have occurred in the vertical region where we lack data. Nevertheless, N_i and IWC for small particles show much larger variability during IMPACTS than during HALO-(AC)³, regardless of the distance to cloud top.

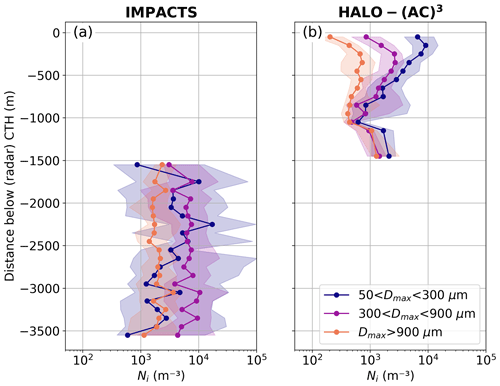
Figure B1 Distribution of ice number concentration N_i as a function of distance to cloud top height (CTH, derived by radar) for (a) IMPACTS and (b) HALO-(AC)³. Lines and markers show median values, while 25 %–75 % quantiles are shaded. Contributions of small (50–300 µm), medium (300–900 µm), and large (>900 µm) particles are shown in blue, purple, and orange, respectively.

Figure B2 The same as Fig. B1 but for ice water content (IWC; calculated accounting for riming).

Appendix C: LWP riming calculations

This section shows the need for updrafts to explain the retrieved amounts of riming given the observed LWPs. We use simple calculations based on Fitch and Garrett (2022). Assuming that a particle collects rime by falling through a liquid layer, the mass of rime accumulated can be approximated by

$$\begin{array}{}\text{(C1)}& m_{\text{rime}}=A_{\mathrm{p}}{E}_{\mathrm{c}}\text{LWP},\end{array}$$

where A_p is the cross-sectional area of the particle, E_c is the combined collection and collision efficiency, and LWP is the liquid water path of the liquid layer. By inserting the definition of M; approximating A_p by a power law function of D_max with prefactor a_A and exponent b_A following Maherndl et al. (2023a); and solving for LWP, we derive

$$\begin{array}{}\text{(C2)}& \text{LWP}={\displaystyle \frac{M{m}_{\mathrm{g}}}{A_{\mathrm{p}}}}={\displaystyle \frac{\mathit{\pi }{\mathit{\rho }}_{\mathrm{g}}M}{\mathrm{6}{a}_A\left(M\right)}}{D}_{\text{max}}^{\mathrm{3}-b_A\left(M\right)}.\end{array}$$

Here, E_c is assumed to be 1 as a worst-case estimate, although lower values are more realistic in the Arctic (Fitch and Garrett, 2022). Equation (C2) applies only for ice particles that have finished the riming process. It is therefore only applied to HALO-(AC)³ data, where LWC=0 was measured, thus excluding 28 March data, where LWC measurements are not available. Because ice particles occur in PSDs, we apply Eq. (C2) to D₃₂ as a proxy for the characteristic size and the respective M we retrieved for each time step. Compared to LWP observations during 1 and 4 April, the calculated LWP is much higher (Fig. C1). Therefore, it is evident that the particles must have been exposed to the liquid layer multiple times, e.g., by cycling through updraft and downdraft regions.

Figure C1 Normalized histograms of observed and calculated liquid water path (LWP) including medians (dashed lines). Observed LWP are from all 1 and 4 April data points. Calculated LWP were only derived for time steps where LWC=0, such that it can be assumed that no further riming will take place.