Investigation of the characteristics of low-level jets over North America in a convection-permitting Weather Research and Forecasting simulation

In this study, we utilized a high-resolution (4 km) convection-permitting Weather Research and Forecasting (WRF) simulation spanning a 13-year period (2000–2013) to investigate the climatological features of low-level jets (LLJs) over North America. The 4 km simulation enabled us to represent the effects of orography and the underlying surface on the boundary layer winds better. Focusing on the continental US and the adjacent border regions of Canada and Mexico, this study not only identified several well-known large-scale LLJs, such as the southerly Great Plains LLJ and the summer northerly California coastal LLJ, but also the winter Quebec northerly LLJ which received less focus before. All these LLJs reach their peak in the nighttime in the diurnal cycle. Thus, the different thermal and dynamic mechanisms forming these three significant LLJs are investigated in this paper. Inertial oscillation theory dominates in the Great Plain LLJ, and the California coastal LLJ is formed by the baroclinic theory, whereas the Quebec LLJ is associated with both theories. Moreover, the high-resolution simulation revealed climatic characteristics of weaker and smaller-scale LLJs or low-level wind maxima in regions with complex terrains, such as the northerly LLJs in the foothill regions of the Rocky Mountains and the Appalachians during the winter. This study provides valuable insights into the climatological features of LLJs in North America, and the high-resolution simulation offers a more detailed understanding of LLJ behavior near complex terrains and other smaller-scale features.

1 Introduction

A low-level jet (LLJ) is described as the fast-moving air ribbon located in the lower atmosphere most of the time (Bonner, 1968; Rife et al., 2010). Many of the world's LLJs have been studied, such as the Great Plains LLJ over the central US (Bonner, 1968; Zhong et al., 1996), the Somali LLJ over eastern Africa (Munday et al., 2021), and the South American LLJ over the east Andes mountains (Montini et al., 2019). Other studies extend beyond inland LLJs to encompass offshore coastal LLJs such as the California LLJs (Parish, 2000) and North African Coastal LLJ (Soares et al., 2018). As a kind of mesoscale weather system, an LLJ has a relatively small vertical range of usually only a few hundred meters, but its width can reach several hundred kilometers. LLJs are closely related to precipitation and even extreme events, and they can transfer abundant water vapor to the downwind regions, providing favorable dynamic conditions for rainfall (Walters and Winkler, 2001; Hodges and Pu, 2019). Meanwhile, researchers have long been interested in investigating their features because LLJs also affect various processes such as wind power development, air pollution transportation, and urban heat islands; the wind turbines would be influenced by positive wind shear and downward entrainment from the LLJs above them, assisting in extracting energy from the strong wind belt inside LLJs (Gadde and Stevens, 2021; Ma et al., 2022). LLJ-related horizontal transportation is beneficial for pollutant removal (Sullivan et al., 2017). The LLJs can enhance the turbulent mixing in the boundary layer, thereby decreasing the atmospheric stability, helping pollution diffusion, and weakening urban heat island intensity (Hu et al., 2013).

Since the mid-20th century, scientists have used regular rawinsonde observations to investigate the characteristics of LLJs. Applying rawinsondes to investigate the Great Plains LLJ in the central US, Bonner (1968), Mitchelle et al. (1995), and Walters et al. (2008) studied its distribution, seasonal activity, horizontal and vertical structure, and diurnal features and established the climatology of the Great Plains LLJ during warm seasons. As well as rawinsondes, radar systems and wind profilers are useful tools for characterizing LLJs. Frisch et al. (1992) observed a typical LLJ process using Doppler weather radar in North Dakota and identified that the friction on the surface of the boundary layer is important in the early stages of LLJ development. Using long-term wind profiler measurement, Miao et al. (2018) interpreted the climatology of LLJs in Beijing and Guangzhou, concluding that the frequency values of LLJs in these two cities are 13.0 % and 4.9 %, respectively. Moreover, Smith et al. (2019) used the Plains Elevated Convection at Night (PECAN) observations to conduct high-quality measurements of nocturnal LLJs with wide spatial and temporal resolutions. They found that sudden changes in LLJ structure typically result from the spatial evolution of the LLJ.

However, there are some disadvantages of observational research that should be noted. First, regular rawinsonde data only contain measurements at two daily time points (00:00 and 12:00 UTC) which cannot fully capture the LLJs' diurnal variations. The time density of observations is therefore coarse, and coastal areas lack regular high-density measurements, making the study of coastal LLJs challenging (Mitchell et al., 1995). Second, heterogeneities in the rawinsonde records, such as variations in station locations, radiosonde types, and archiving procedures, may also complicate the use of these observations in climate research. Third, rawinsonde measurements taken at a single point are not able to capture horizontal shear and environmental conditions (Chen et al., 2005), although observation platforms such as radar, PECAN, or lidar which investigate the atmosphere as low as 300 m can compensate for this lack of observational data to some extent. As well as lidar that investigates the atmosphere as low as 300 m, these approaches are still limited by the spatial coverage of their measurement platforms (Smith et al., 2019).

Because of these problems with observational methods, researchers have chosen reanalysis datasets as an alternative for investigating LLJs. Reanalysis data have relatively better spatial and temporal coverage than rawinsonde measurements, incorporate observations into the preliminary model simulations, provide more comprehensive variables through assimilation, and contain broader domains. Rife et al. (2010) highlighted the global distribution of identified nocturnal LLJs using reanalysis data with a horizontal grid spacing of 40 km and even successfully extracted some previously unknown jets, like the Tarim nocturnal LLJ in northwestern China, the Ethiopia nocturnal LLJ, and the Namibia–Angola nocturnal LLJ. Doubler et al. (2015) applied the North American Regional Reanalysis (NARR) dataset (∼ 32 km) to generate long-term LLJ climatology in North America. Consistent with previous records, the results of Doubler et al. (2015) supplemented the description of some smaller-scale LLJs. Similarly, Montini et al. (2019) compared and validated the performance of five different reanalysis datasets in identifying LLJs. Their results showed the 38-year climatology of South American LLJs with ERA-Interim data (∼ 79 km).

Scientists have also conducted studies based on numerical simulations, which can more accurately represent LLJs than reanalysis datasets, especially in the vertical direction, thereby yielding new insights into LLJ features. Tang et al. (2017) used an ensemble of dynamically downscaling regional climate simulations to generate the climatology of Great Plains LLJ and predicted that the LLJ will occur more frequently during the nighttime in spring and summer in the mid-21st century. Jiménez-Sánchez et al. (2019) conducted a simulation for LLJs over the Orinoco Basin through the dynamic downscaling of the Weather Research and Forecasting model (WRF). The simulation represented the jet streaks better than previous studies within a broader region of wind enhancement and illustrated more detailed diurnal evolution. Nevertheless, most general numerical simulations still represent the convective processes by the parameterization scheme, which generates uncertainty in the results. These issues can be addressed using convection-permitting models with grid spacing under 5 km that adequately simulate the convections and other small-scale processes (Liu et al., 2017; Li et al., 2019; Kurkute et al., 2020). Convection-permitting modeling describes the underlying surface more accurately than coarse-resolution simulations and reanalysis data and shows its ability in investigations of LLJs near complex mountain areas. Du and Chen (2019) analyzed the LLJs over southern China using 4 km WRF model and revealed a solid relationship between the mesoscale lifting of LLJs and the convection's initiation. They also highlighted the importance of the coastal terrain. Overall, the finer-resolution tools tend to show more comprehensive and precise results, offering detailed and accurate references to LLJs.

The formation mechanisms of LLJs have been studied extensively by researchers. In explaining the diurnal cycle feature of the Great Plains LLJ, the inertial oscillation theory proposed by Blackadar (1957) and Stensrud (1996) suggests that the LLJ is related to the friction change in the boundary layer. During the night, the jet core wind is enhanced after decoupling with near-surface friction. Holton (1967) and Parish (2000) developed the thermal wind adjustment theory, which suggests that the horizontal pressure gradient changes because the atmosphere over the sloping terrain is warmer or because the sea–land contrast influences the diurnal cycle of wind. Additionally, LLJs can also be formed due to synoptic system forcing, as proposed by Uccellini et al. (1987) and Saulo et al. (2007). However, convection-permitting models can help explain how LLJs form because they have precise descriptions of weather systems and underlying orography. Using 4 km simulations, Fu et al. (2018) and Zhang et al. (2019) analyzed the evolution of LLJs over mountainous areas in eastern and southwestern China, respectively. They concluded that inertial oscillation plays a prominent role in and is responsible for the local precipitation peak at a certain time. Besides, Shapiro et al. (2016) argued that the formation of some LLJs may not be impacted by a single factor and that a unified theory analysis is thus required. Thus, a dataset that offers more information must be very popular. All these studies have shown that convection-permitting models, with both finer coverage and resolutions, are a powerful tool for LLJ characteristic research.

In this study, we utilize the 4 km convection-permitting WRF simulation (Liu et al., 2017) to analyze the features of low-level jet systems across North America, improving the spatial and temporal resolutions. Section 2 introduces the model configuration and the criteria for LLJ identification, Sect. 3 presents the characteristics of LLJ frequencies in North America, and Sect. 4 illustrates the analysis of the background and mechanisms in several LLJ cases. Finally, Sect. 5 provides the discussion and conclusion.

2 Model configuration and methods

2.1 WRF setup

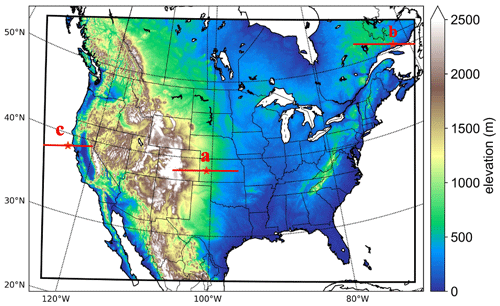
This study utilized a convection-permitting Weather Research and Forecasting (WRF) dataset (Liu et al., 2017; data are available at https://rda.ucar.edu/datasets/ds612.0/, last access: 18 October 2022) with a horizontal resolution of 4 km over North America, without nesting. The domain covers the entire continental US, southern Canada, and northern Mexico, as illustrated in Fig. 1. The simulation provides three-dimensional data at a temporal resolution of 3 h, resulting in eight time steps per day. In the vertical direction, the data have 51 eta levels and can reach 50 hPa. It should be noted that there are five layers under 500 m height, and nine layers under 1 km are outputted above ground level, which means the WRF has a better ability than other coarse modeling to capture the LLJs occurring in the boundary layer. Considering the computational cost for high-resolution modeling, this simulation period spans from 1 October 2000 to 30 September 2013, and the 6 h ERA-Interim reanalysis dataset of 0.7° resolution was used as input for the climate simulation. The vertical layer depth of the forcing ERA-Interim data under 5 km is about 0.3–1.4 km (Hoffmann and Spang, 2022). Even though the version is older, the ERA-Interim dataset has still been maturely applied in the climate modeling study and has accumulated a wealth of related cases and experiences (Liu et al., 2017; Li et al., 2019). Besides, it is noted that 13 years is shorter than the normally defined climatology, but considering the computational cost of high-resolution simulation, it is still a balanced compromise. This shorter period length was also utilized to analyze the climate features of other weather events (Liu et al., 2017; Ma et al., 2022). The simulation did not apply any cumulus parameterization scheme due to the fine horizontal grid spacing, but other sub-grid-scale processes were parameterized by various physical schemes. The rapid radiative transfer model (RRTMG) (Iacono et al., 2008) was used for simulating longwave and shortwave radiations, the Yonsei University (YSU) scheme was used for representing the planetary boundary layer (Hong et al., 2006), and the Noah-MP (multiparameterization) model was used for computing surface processes (Niu et al., 2011). In this study, the planetary boundary layer scheme is retained. Nonetheless, it should be noted that this would introduce uncertainties to the simulation in the vertical direction, especially in regions with complex topography.

Figure 1 Study domain of this convection-permitting model. The colors represent the elevation. The red lines and stars show the positions of investigated cross section and jets in Sect. 4.

2.2 Methodology

Using the threshold criteria proposed by Bonner (1968), this study identifies LLJs from the vertical wind profile of each grid point in the model output data. LLJs are present when the following conditions are met: (1) the height of the LLJ core maximum wind speed is below 3 km above ground level (AGL); (2) the maximum wind speed is greater than or equal to 12 m s⁻¹; (3) from the height of the wind maxima to the height of the next minimum value or 3 km height (whichever is lower), the velocity of the wind drops by at least 6 m s⁻¹; and (4) the wind speed drops by at least 6 m s⁻¹ below the level of wind maxima. On the other hand, the investigation of LLJs is normally conducted with different jet core wind directions. Pu and Cook (2010) studied the West African westerly jet; this zonal LLJ can help transport water vapor from the Atlantic to Africa, and this LLJ is related to the westward extension of the continental thermal low pressure over Africa in summer. Thus, the LLJ research should refer to the local climatologic or geographic features. Considering the importance of the meridional LLJ for heat and water vapor transport over North America, as well as the direction of the Rockies, this study addresses LLJ frequencies in different meridional directions. According to Walter et al. (2008) and Doubler et al. (2015), the criteria for identifying different meridional LLJs are as follows: for southerly LLJs (S-LLJs), the jet core wind direction is between 113 and 247°, and for northerly LLJs (N-LLJs), the jet core direction is between 293 and 67°. These criteria are also used in this study.

Based on the identification criteria above, we determined if the LLJ existed at each grid point and consequently counted the occurrences of S-LLJs and N-LLJs. We also calculated the frequencies of LLJs in different seasons or time steps. The frequency is defined as the percentage of the total number of occurrences for the selected accumulation period. We generated the frequency distribution maps for LLJs in North America, which are illustrated in Sect. 3.

3 The patterns of North American LLJs

3.1 Analysis of atmospheric circulation

This study adopts model data to capture the climatological features of LLJs in North America. Considering the relationship between LLJs and synoptical systems, we evaluated the ability of the convection-permitting model to simulate the background atmospheric circulation. Figure 2 depicts the simulated multi-year analysis of geopotential heights at 500 hPa and sea level pressure isobars for summer and winter. In summer, at a height of 500 hPa (Fig. 2a), the model depicts a trough in the east of the continental US, a ridge over the Rocky Mountains, and the upper-air subtropical anticyclone crossing the southern US. At sea level (Fig. 2b), the model captures the Azores high-pressure area in the Atlantic Ocean and the Hawaiian high-pressure area in the Pacific.

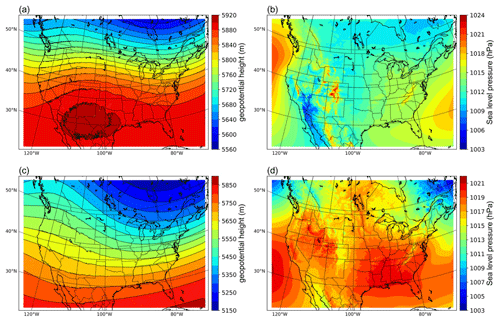
Figure 2 Multi-year patterns of atmospheric circulations simulated by the convection-permitting model: (a) summer 500 hPa geopotential height, (b) sea level pressure in summer, and (c–d) the same variables but in winter.

In winter, the contours at the pressure value of 500 hPa (Fig. 2c) show stronger fluctuating characteristics. The eastern trough and western ridge over the continent strengthen, and the polar vortex extends to the northern US, while most of North America is controlled by a cold high-pressure system. In addition, the subtropical anticyclone is too weak to be found within the study domain. On the other hand, most of North America is controlled by a cold high-pressure system at sea level (Fig. 2d), and parts of the Icelandic Low and Aleutian Low appear on both the east and west of Canada, even though their centers are not captured in the domain. To summarize, the convection-permitting model can simulate the features of semi-permanent centers of atmospheric circulations in North America, thus demonstrating its strength in identifying the LLJs in this area.

3.2 Seasonal variations in LLJs

3.2.1 Northerly LLJs

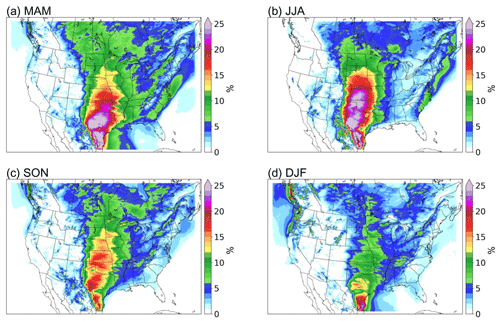
Figure 3 illustrates the seasonal frequency distribution of northerly low-level jets (N-LLJs). The frequency is defined as the ratio of the total number of LLJ occurrences to the total number of time steps in each season. Notably, the California coastal LLJ peaks during the summer months (June, July, and August (JJA)), where frequencies exceed 25 % over a broad area stretching from the southern Oregon coast to central California. In these regions, frequencies above 5 % can even extend into the Pacific Ocean near northern Baja California. However, when transitioning from summer to autumn (September, October, and November (SON)), there is a sharp decline in the frequency of this LLJ as it drops to only 5 %–15 % within the core region, which is predominantly along the northern California coast. In winter (December, January, and February (DJF)), occurrences are sparse, at approximately 1 %–2 %.

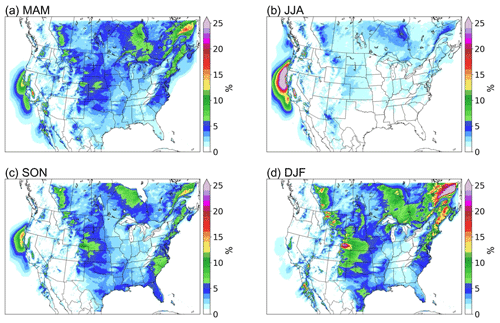
Figure 3 Seasonal occurrence frequency of N-LLJs. Frequency shown here is calculated by counting the number of occurrences of LLJs in each 3 h time step and then dividing the total number of LLJs in each season by the number of time steps in that season.

Conversely, various N-LLJ phenomena are more prevalent during the colder seasons. These jets primarily occur near the eastern slopes of significant terrains such as the Rocky Mountains, Appalachian Mountains, and the Quebec–Labrador Plateau. High frequencies (> 10 %) are observed from western Alberta to Oklahoma during winter, with hot spots sporadically located in Alberta, Montana, Wyoming, and Colorado, where frequencies reach about 20 %, particularly between Colorado and Wyoming. In more than 25 % of the wind profiles analyzed, N-LLJs were identifiable. Along the eastern US coast, N-LLJs predominantly stretch from Maine to South Carolina, with peak frequencies of approximately 15 %–20 %. In eastern Quebec, N-LLJs are most frequent in winter, exceeding 25 %. The simulation also detects the presence of N-LLJ in about 10 % of the time steps over Hudson Bay. Notably, the frequencies of all of the aforementioned N-LLJs significantly diminish in spring, becoming scarcely detectable in summer, with frequencies mostly under 5 %.

3.2.2 Southerly LLJs

As to the patterns of S-LLJs in different seasons (see Fig. 4), during winter, frequencies exceeding 10 % are observed across a vast area spanning from south Texas and the western Gulf of Mexico to southern Iowa, depicted as a deep green area in Fig. 4d. The greatest frequencies of S-LLJs (> 20 %) are found along the border between northeastern Mexico and the United States. In addition, about 15 % of the simulated wind profiles in south–central Texas are identified as S-LLJs (red clusters). In the spring (March, April, and May (MAM)), the frequency expands significantly in > 10 % of areas, with clear S-LLJ distributions detected in Manitoba, Saskatchewan, and other parts of Canada. The highest frequencies are still found in the Texas–Mexico area, where the magnitude of these frequencies increases to over 25 %. This region (colored purple) also extends northward to occupy most of Texas. In winter, S-LLJs with occurrence frequencies of above 15 % extend to near Colorado and Nebraska.

By summer, the area with frequencies greater than 10 % no longer reaches the central Canadian prairie provinces. The S-LLJs over the western Gulf of Mexico become nearly indiscernible in modeled data, with frequencies approaching 0 %. Conversely, the area with frequencies exceeding 25 % expands northward and is segmented into three distinct parts: along the northeastern Mexico–Texas border, west–central Texas, and the central US Great Plains (western Oklahoma and southern Kansas). Regions where over 15 % of wind profiles are identified as S-LLJs also spread from Colorado to near South Dakota.

In the fall, the magnitude of the frequency of S-LLJs decreases dramatically in the central US Great Plains and Texas. The frequency still maintains a level greater than 15 % in most areas, but with a maximum frequency of only 20 %, and is sporadically located in southwestern Texas. The frequencies greater than 10 % again expand northward and eastward in this season, reaching Manitoba and Ontario.

Additionally, several smaller-scale S-LLJs are evident on the seasonal S-LLJ distribution map. In spring, a narrow region of S-LLJs with a frequency greater than 5 % along the eastern side of the Appalachians extends from Georgia through the western Atlantic to southern Nova Scotia. Near eastern Maryland over the Atlantic, the frequency of S-LLJs can exceed 10 %. This narrow frequency belt persists through summer with the same coverage, though the frequency magnitude diminishes, and the presence of frequencies greater than 10 % is no longer visible. In winter, a region where S-LLJ frequency exceeds 5 % stretches from southwestern Oregon to the west coast of British Columbia, Canada. However, by spring, S-LLJs with frequencies above 5 % occur solely over the ocean west of British Columbia, and in summer, S-LLJs are virtually undetectable in this region.

Figure 4 Seasonal frequency of S-LLJs.

To summarize, for the LLJ systems that have been investigated by many researchers, the convection-permitting WRF model performs well in observing the Great Plains S-LLJ and California coastal N-LLJ during the summer. But as for the winter LLJs that lack attention, it is essential to compare and validate the occurrence and features revealed by WRF simulation. Therefore, the ERA5 reanalysis dataset is applied in this study to capture the LLJs in winter using the same criterion. Appendix A shows the results of the comparison between the ERA5 and WRF simulation.

3.3 Diurnal variations in LLJs

To show the diurnal features of the LLJs, we selected summer and winter as the representative seasons because S-LLJs and N-LLJs occur most frequently in these seasons, respectively. Below, the descriptions are divided into N-LLJs and S-LLJs.

3.3.1 Northerly LLJs

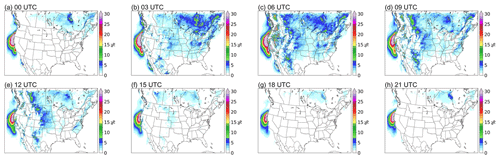
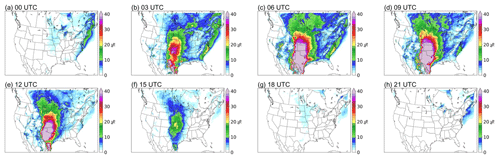
The California coastal N-LLJ is the most highlighted low-level jet system in this region in summer. As seen in Fig. 5, it occurs throughout the day over the eastern Pacific Ocean from Oregon to the California coast. Figure 5 also shows that the California Coastal N-LLJ has diurnal characteristics. From 21:00 UTC (13:00 LST in California), the low-level jet begins to develop, with a N-LLJ frequency of > 30 %, expanding until it reaches its maximum at 03:00–06:00 UTC. Then the high-frequency coverage of the California coastal LLJ gradually shrinks, reaching the minimum at 18:00 UTC and only existing off the northwestern coast of California.

Figure 5 Diurnal frequency of N-LLJs in the summer (JJA).

In winter (Fig. 6), three types of N-LLJs over the Hudson Bay Lowlands, the eastern slopes of the Quebec–Labrador Plateau, and the Appalachians display similar diurnal fluctuations. All three N-LLJs reach their highest frequency at 03:00 UTC (22:00 EST) and their lowest at 18:00 UTC (13:00 EST). The only difference among the three types is that the smallest frequency of the Quebec N-LLJ still endures at a level of greater than 15 %, while the other two N-LLJs mostly have frequencies of about 5 %. The smallest frequency (∼ 5 %) of N-LLJs occurs downstream the Rocky Mountains (over Alberta, Montana, and Kansas) at 21:00 UTC. In the subsequent development stage, the changes in the sporadic hot spots distributed near the eastern boundary of the Rocky Mountains are more significant. As seen in Fig. 6, frequency starts growing from 00:00 UTC and then peaks at 12:00 UTC, especially the wind maxima located in Colorado, Wyoming, and Kansas, where the highest frequency can be > 25 %.

Figure 6 Diurnal frequency of N-LLJs in winter (DJF).

3.3.2 Southerly LLJs

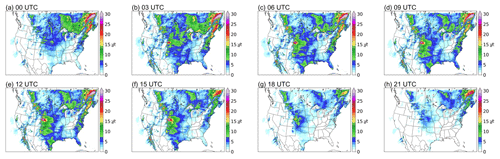
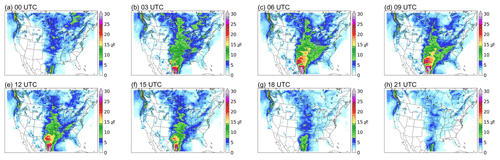
In summer, the Great Plains S-LLJ occurs more frequently than in other seasons, and its diurnal variability is also the strongest in this season (see Fig. 7). At noon local time and in the afternoon (18:00–00:00 UTC; 12:00–18:00 CST), almost no S-LLJs occur over the central US (frequency < 5 % or about 0 %). In contrast, the Great Plains LLJ begins to develop at 03:00 UTC, when a frequency of over 25 % extends from Mexico to Kansas. It reaches maximum strength at midnight (06:00–09:00 UTC; 00:00–03:00 CST), when the frequency reaches over 30 %, and the high-frequency coverage enlarges to the Dakotas, the border of the eastern Rocky Mountains, and western Minnesota, Missouri, and Louisiana. Summer S-LLJs are also active in southern Canada at night and in the early morning. In Saskatchewan, Manitoba, and central Ontario (03:00–12:00 UTC; as shown in Fig. 7), S-LLJs are found with frequency > 15 %. In the eastern US and Atlantic, S-LLJs occur most frequently at midnight (03:00–06:00 UTC).

Figure 7 Diurnal frequency of S-LLJs in summer (JJA).

For the cold season (Fig. 8), even though the Great Plains LLJ is the most inactive based on the description in Sect. 3.2, it still has a clear diurnal variation. Compared with the results in summer, the diurnal cycle of the Great Plains LLJ in winter is not that pronounced. It mainly occurs over the western Gulf of Mexico and southern Texas, with the frequency in the afternoon (18:00–21:00 UTC) declining to 5 %–10 %. The S-LLJ develops from 03:00 UTC, gradually generating two high-frequency (20 %–25 %) centers in mid- and southeastern Texas at 06:00–12:00 UTC. As for the S-LLJ near Vancouver Island, it is hard to see the diurnal variability. There is only a slight magnitude growth of frequency from the afternoon (00:00 UTC) to the evening (06:00 UTC), and the coverage is almost the same.

Figure 8 Diurnal frequency of S-LLJs in winter (DJF).

4 Formation and evolution mechanisms of various LLJs

Section 3's results illustrate the occurrence frequency of LLJs over North America, particularly their seasonal and diurnal features. To explain the mechanisms, the inertial oscillation theory from Blackadar (1957) is used. Using this theory, we start from the horizontal momentum equations and divide the actual horizontal wind $u/v$ into two components – geostrophic wind $u_{\mathrm{g}}/v_{\mathrm{g}}$ and ageostrophic wind $u_{\mathrm{a}}/v_{\mathrm{a}}$ – as follows:

$$\begin{array}{}\text{(1a)}& {\displaystyle \frac{\mathrm{d}(u_{\mathrm{g}}+u_{\mathrm{a}})}{\mathrm{d}t}}=-{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\partial P}{\partial x}}+f\left(v_{\mathrm{g}}+v_{\mathrm{a}}\right),\text{(1b)}& {\displaystyle \frac{\mathrm{d}(v_{\mathrm{g}}+v_{\mathrm{a}})}{\mathrm{d}t}}=-{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\partial P}{\partial y}}-f\left(u_{\mathrm{g}}+u_{\mathrm{a}}\right),\end{array}$$

in which ρ is air density, P is pressure, and f is the Coriolis parameter. Assuming that the horizontal pressure gradient is fixed, the geostrophic wind is a constant as well, which means $\frac{\mathrm{d}{u}_{\mathrm{g}}}{\mathrm{d}t}=\frac{\mathrm{d}{v}_{\mathrm{g}}}{\mathrm{d}t}=\mathrm{0}$,

$$\begin{array}{}\text{(2a)}& {\displaystyle \frac{\mathrm{d}{u}_{\mathrm{a}}}{\mathrm{d}t}}=-{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\partial P}{\partial x}}+f\left(v_{\mathrm{g}}+v_{\mathrm{a}}\right),\text{(2b)}& {\displaystyle \frac{\mathrm{d}{v}_{\mathrm{a}}}{\mathrm{d}t}}=-{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\partial P}{\partial y}}-f\left(u_{\mathrm{g}}+u_{\mathrm{a}}\right).\end{array}$$

When the definition of geostrophic wind $u_{\mathrm{g}}=-\frac{\mathrm{1}}{\mathit{\rho }f}\frac{\partial P}{\partial y}$ and $v_{\mathrm{g}}=\frac{\mathrm{1}}{\mathit{\rho }f}\frac{\partial P}{\partial x}$ are combined, Eq. (2) is

$$\begin{array}{}\text{(3a)}& {\displaystyle \frac{\mathrm{d}{u}_{\mathrm{a}}}{\mathrm{d}t}}=f{v}_{\mathrm{a}},\text{(3b)}& {\displaystyle \frac{\mathrm{d}{v}_{\mathrm{a}}}{\mathrm{d}t}}=-f{u}_{\mathrm{a}}.\end{array}$$

If $\frac{\mathrm{d}}{\mathrm{d}t}$ is taken to both sides of Eqs. (3), then we get $\frac{{\mathrm{d}}^{\mathrm{2}}{u}_{\mathrm{a}}}{\mathrm{d}{t}^{\mathrm{2}}}=-f^{\mathrm{2}}{u}_{\mathrm{a}}$, and $\frac{{\mathrm{d}}^{\mathrm{2}}{v}_{\mathrm{a}}}{\mathrm{d}{t}^{\mathrm{2}}}=-f^{\mathrm{2}}{v}_{\mathrm{a}}$, thereby

$$\begin{array}{}\text{(4a)}& {\displaystyle }{u}_{\mathrm{a}}=c_{\mathrm{1}}\cos \left(ft\right)+c_{\mathrm{2}}\sin \left(ft\right),\text{(4b)}& {\displaystyle }{v}_{\mathrm{a}}=c_{\mathrm{2}}\cos \left(ft\right)-c_{\mathrm{1}}\sin \left(ft\right).\end{array}$$

Therefore, according to Eq. (4), the ageostrophic wind should theoretically have a circular pattern variation, and the vector must rotate clockwise with a period of 2$\mathit{\pi }/f$ (Blackadar, 1957; Van de Wiel et al., 2010). Under the condition of a constant geostrophic wind – when the ageostrophic vector rotates from the opposite to the same direction of geostrophic wind – the wind transitions from subgeostrophic to supergeostrophic. This change occurs because of decoupling with surface friction effects, and then the wind gets unbalanced.

Other theories also help explain the formation of LLJs, such as the sloping-terrain thermodynamic mechanism (Holton, 1967) and background synoptic system forcing (Uccellini et al., 1987). To understand the characteristics of the LLJs in this study, three typical cases are analyzed: Great Plains S-LLJ, Quebec N-LLJ, and California coastal N-LLJ. The locations for extracting data are shown in Fig. 1 (solid lines and stars labeled a, b, and c).

4.1 Great Plains S-LLJ

As Sect. 3's results show (see Fig. 7), the Great Plains S-LLJ typically occurs in summer and more frequently at night. To investigate its associated meteorological condition, this study extracts all the Great Plains S-LLJ cases that occur at the jet core in JJA. The jet core is defined by where the mean meridional wind is the strongest on the cross section, and it locates at star A (shown in Fig. 1). The mean sea level pressure and 800 hPa geopotential height are shown in Fig. 9a and b, respectively. The background large-scale circulations indicate that, at all the time points when the Great Plains S-LLJ occurs, the range of the subtropical anticyclone extends east of the Great Plains at both ground and low-level atmosphere. A high-pressure ridge is located near the Gulf Coast of Mexico and Texas (Fig. 9b). Thus, clearly, the zonal pressure/geopotential gradient in the central US guides the dominant southerly winds around this region. The cross section in Fig. 9c illustrates a strong baroclinicity and shows that the isentropic line incline moves from east to west, as is typical of the sloping-terrain heating effect (Holton, 1967). This effect generates an upslope wind on the east side of the slope, and the airstream gradually turns northward due to the Coriolis force, creating the southerly LLJs. On the other hand, as can be seen in the frequency cycle in Fig. 9d, at noon local time (at the selected point (a) in Fig. 1), the frequency of the Great Plains LLJ is very low (close to 0 %) and rises to more than 40 % after 18:00 LST, even if the radiation is not at the day's peak.

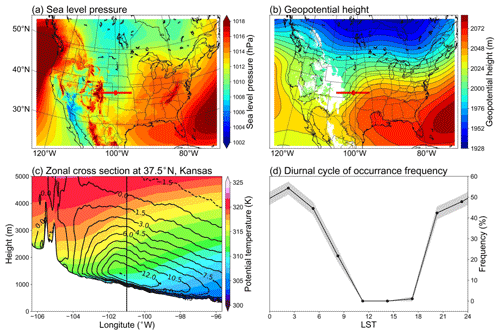
Figure 9 Background circulations of the Great Plains S-LLJ in JJA: (a) sea level pressure; (b) geopotential height of 800 hPa; (c) cross section, including meridional winds (lines) and potential temperature (shading); and (d) diurnal cycle of frequency, with the shaded 95 % confidence intervals. The red lines and points in panels (a) and (b) show the position of the cross section and chosen jet core. The vertical line in panel (c) shows the zonal location of the chosen jet core.

To explain the nighttime enhancement of S-LLJ, we analyzed the wind vectors using the inertial oscillation theory. To show more significant diurnal variation, all the time points, including the LLJs that did not occur, were considered. Figure 10a is the hodograph of jet core winds at point (a) near the Great Plains, and their temporal mean is computed at 3 h intervals in summer. It is noted here that the “jet core” means the position where the LLJ occurs horizontally most frequently on the cross section. Compared with the mean actual wind (blue arrow), the deviation at each local time shows a clear clockwise rotation. The wind speed begins increasing after 17:00 LST. Nevertheless, the analysis for Fig. 9 indicates the sloping heating effect, meaning that the geostrophic wind is not fixed.

Thus, to obtain the ageostrophic winds, we computed the geostrophic components by pressure gradient and subtracted them from the actual airflow. According to the aforementioned definition of geostrophic wind, u_g and v_g are calculated by the horizontal pressure gradient $\frac{\partial P}{\partial y}$ and $\frac{\partial P}{\partial x}$, respectively. By choosing four grids surrounding point (a), we first interpolated the pressure value to the same level as the LLJ core height. Then, we adopted the central difference equation $\frac{\mathrm{\Delta }P}{\mathrm{\Delta }x}=\frac{P_{i+\mathrm{1}}-P_{i-\mathrm{1}}}{x_{i+\mathrm{1}}-x_{i-\mathrm{1}}}$ or $\frac{\mathrm{\Delta }P}{\mathrm{\Delta }y}=\frac{P_{i+\mathrm{1}}-P_{i-\mathrm{1}}}{y_{i+\mathrm{1}}-y_{i-\mathrm{1}}}$ to obtain the pressure gradients at point (a), where i is the index of the grid point at point (a).

Figures 10b and c display geostrophic wind vectors (blue arrows) and ageostrophic vectors (pink) at noon and midnight. The southerly geostrophic flows are much stronger in the afternoon (Fig. 10b) than at midnight. The ageostrophic winds flow mostly in the opposite direction, limiting the actual wind speed. At night (Fig. 10c), the geostrophic wind direction rotates clockwise from that of the afternoon as the pressure gradient changes. Considering the relative positions of blue and pink vectors at 23:00 and 01:00 LST, ageostrophic flow has rotated roughly 150° to enhance the geostrophic winds, thereby creating a supergeostrophic state. Although the inertial oscillation theory can help explain some aspects of wind behavior, the real situation is more complex than initially thought. Figures 10b and c indicate that by 02:00 LST, the wind is almost entirely geostrophic with only negligible ageostrophic perturbations. This suggests that the diurnal changes in the geostrophic wind and pressure gradient may provide a complicating background that prevents the inertial oscillation theory from fully prevailing. While the inertial oscillation theory can provide valuable insights, it should not be relied upon as the sole explanation for LLJs at the Great Plains. Instead, a more comprehensive understanding of atmospheric dynamics is necessary to fully comprehend the behavior of the wind, particularly when dealing with diurnally changing conditions. Figure 10d compares different meridional wind components' amplitudes. The geostrophic wind contributes significantly to the southerly wind during the day, peaking at 14:00 LST (blue bars). The northerly ageostrophic wind (red bars) is highest during the day, indicating the strongest negative impact from friction. The meridional ageostrophic component decreases and eventually reverses at 23:00 LST, showing a process from sub- to supergeostrophic status. In summary, the thermodynamic circulation near the slopes of the Great Plains contributes to the strong southerly airflow, while the inertial oscillation plays a critical role in forming the nocturnal southerly LLJ.

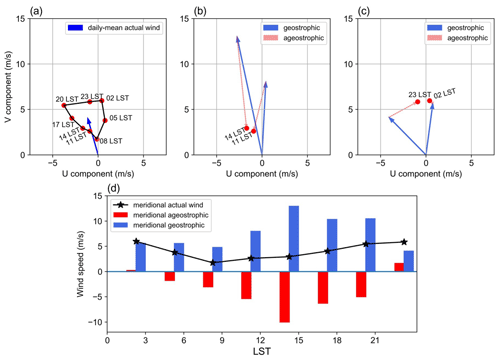
Figure 10 (a) Hodograph of jet core winds for the Great Plains S-LLJ every 3 h over the whole JJA (red dots; solid line) and the daily averaged actual wind velocity (blue vector). Vectors of mean jet core geostrophic winds (solid blue) and ageostrophic winds (dashed red) at (b) 11:00/14:00 LST and (c) 23:00/02:00 LST. (d) Diurnal cycles of meridional components of actual (black line), geostrophic (blue bars), and ageostrophic winds (red bars).

4.2 Quebec N-LLJ

Similarly, for the Quebec N-LLJ that is typically observed in winter, we selected all the LLJ cases at point (b) (see the position in Fig. 1) in DJF to generate the background circulation pattern. The background large-scale circulations indicate that the northeastern coast of Canada lies to the west of a strong surface low-pressure system (Fig. 11a), while in the lower troposphere, a ridge on the east side of Hudson Bay occupies the Labrador Plateau (Fig. 11b). This combination brings the northerly momentum to the downstream eastern coast. In fact, the background circulation is consistent with the shallow baroclinic structure of Quebec N-LLJ in winter, that is, the thermal difference between relatively warm sea and cold land. The cross section in Fig. 11c shows the thermodynamic structure of this N-LLJ. A well-defined low-level jet core is located above land and close to the coastline (approximately 63° W). With a maximum wind speed of more than 16 m s⁻¹ and a height of about 400 m, the jet core is located above the mixed layer under the warm air covering and on the land side. Notably, the steep isentropic lines slope towards the ocean and finally sink at the position of 60° W. The onshore isentropic lines are flat and dense above the LLJ core, which means the environment is quite stable. This is helpful to maintain the structure of the LLJ when vertical motion is inhibited and horizontal wind is enhanced. Compared with the sloped isentropic lines in the Great Plain S-LLJ case (Fig. 9c), the stability over the Great Plain is not as high as in this case, so this difference in stability helps explain the variation in wind speeds between these two cases.

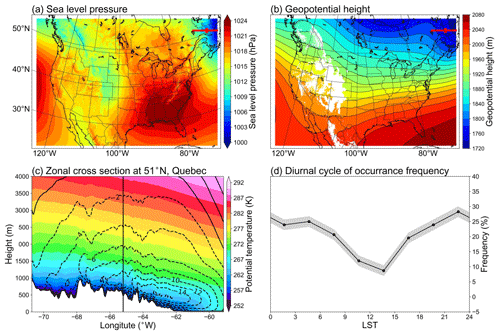
Figure 11 Background circulations of the Quebec N-LLJ in DJF: (a) sea level pressure; (b) geopotential height of 800 hPa; (c) cross section, including meridional winds (lines) and potential temperature (shading); and (d) diurnal cycle of frequency, with the shaded 95 % confidence intervals. The red lines and points in panels (a) and (b) show the position of the cross section and chosen jet core. The vertical line in panel (c) shows the zonal location of the chose jet core.

In addition, the diurnal cycle of frequency (Fig. 11d) shows that the diurnal signal and peak frequency of Quebec N-LLJ are much weaker than the Great Plains S-LLJ, becoming weakest at noon and peaking at midnight, which is consistent with the results reported in Sect. 3. This diurnal variation can be explained by the baroclinicity near this region. At night in winter, the land temperature drops faster than the ocean temperature due to radiative cooling, enhancing the land–sea contrast and thereby the thermal wind above. The gentle slope on the east of the Labrador Plateau could generate the slope heating effect in the daytime. In this way, the related temperature gradient from east to west offsets the land–sea thermal difference.

As for the impact of inertial oscillation on the Quebec N-LLJ, the hodograph of averaged 3 h winds extracted at point (b) (Fig. 12a) also illustrates a clear clockwise rotation of wind deviations compared with the daily mean (blue arrow). Figure 12b and c show that the geostrophic and ageostrophic wind vectors contribute to the diurnal cycle in the afternoon and morning, respectively. Even though the direction of geostrophic wind changes significantly, the relative angles between ageostrophic and geostrophic arrows indicate that the ageostrophic flow rotates clockwise. The geostrophic wind is weakened by ageostrophic wind in the afternoon (Fig. 12b), whereas the supergeostrophic state is generated in the morning (Fig. 12c).

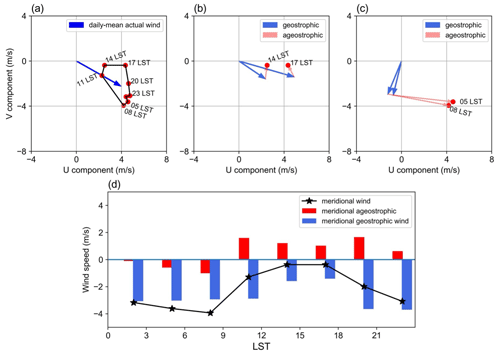
Figure 12 (a) Hodograph of jet core winds for the Quebec N-LLJ every 3 h over the whole DJF (red dots; solid line) and the daily averaged actual wind velocity (blue vector). Vectors of mean jet core geostrophic winds (solid blue) and ageostrophic winds (dashed red) at (b) 14:00/17:00 LST and (c) 05:00/08:00 LST. (d) Diurnal cycles of meridional components of actual (black line), geostrophic (blue bars), and ageostrophic winds (red bars).

Focusing only on the meridional amplitudes validates this characteristic. In Fig. 12d, the blue line that represents the mean actual meridional wind has the same diurnal trend as the frequency variation in Fig. 11d. The northerly wind is weakest in the afternoon, peaking at night and in the early morning. Similarly, the variation in meridional geostrophic flow has a consistent phase with the actual meridional wind, which is explained by the baroclinic structure near the Quebec coast mentioned above. The meridional ageostrophic wind in this region also promotes the formation of N-LLJ. The ageostrophic wind drags the geostrophic component in the afternoon before reversing to a consistent direction with the northerly geostrophic flow at night and in the morning. This trend is also the result of decreasing friction after sunset. Therefore, the evolution of Quebec N-LLJ derives from both inertial oscillation and land–sea thermal contrast in winter.

4.3 California coastal N-LLJ

The California coastal N-LLJ is similar to the one in Quebec, but it occurs more often in summer afternoons or evenings over the ocean. Figure 13a shows that a relatively strong high-pressure system is located on the east coast of the Pacific Ocean, trending NE–SW, although half of the structure is beyond the boundary of the domain. On the 800 hPa isobaric surface in Fig. 13b, there is also an anticyclone system in the same location, whose eastern contour is roughly parallel to the coastline, guiding the airflow to the south. Therefore, this pair is also forced by the thermal difference between land and sea, but contrary to the LLJ in Quebec, in summer, when the California LLJ occurs frequently, it has the characteristics of the cool sea–hot land. Figure 13b also shows that the isobars near Cape Mendocino are relatively strong, making the ridge of high pressure extend northeastward of the Cape. This extension is generally believed to occur due to pressure perturbation caused when northerly winds converge at this position after being obstructed (Rahn and Parish, 2007). Regarding the cross section structure shown in Fig. 13c, the jet core is located at steep isentropic lines above the ocean at a height of 500 m. On the coast of California, the LLJ is close to the mountains. The maximum central wind speed of California coastal LLJ exceeds 20 m s⁻¹, whereas Quebec N-LLJ's max core wind is only about 14 m s⁻¹. Based on baroclinicity, the isentropic lines slope towards the continent and finally sink near the coastline.

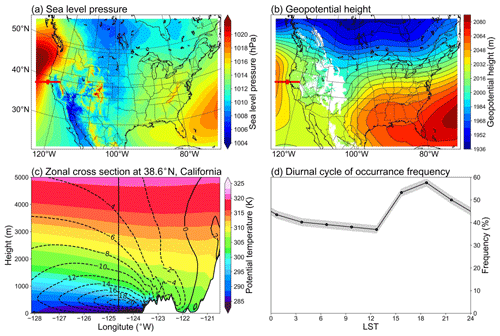
Figure 13 Background circulations of the California coastal N-LLJ in JJA: (a) sea level pressure; (b) geopotential height of 800 hPa; (c) cross section, including meridional winds (lines) and potential temperature (shading); and (d) diurnal cycle of frequency, with the shaded 95 % confidence intervals. The red lines and points in panels (a) and (b) show the position of the cross section and chosen jet core. The vertical line in panel (c) shows the zonal location of the chosen jet core.

The core wind speed in California's coastal LLJ is higher than that of Quebec's LLJ because the land–sea contrast is more significant in summer than in winter and the formed sea breeze front generates flow convergence under the blockage caused by the West Coast mountains. On the other hand, the atmosphere over the sea is more stable because the isentropic lines are flatter and denser than Quebec's case, which also favors the development of LLJ. In contrast, the east coast of Quebec is relatively gentle, which may account for its lower wind speed. California's LLJ occurs frequently at each time step, and its diurnal signal is weaker compared, for example, to the signal in the Great Plain S-LLJ. Moreover, the California signal stays at a frequency of over 35 %. California's LLJ occurs most frequently at around 18:00 LST and starts to decline after sunset, which is generally consistent with the coastal baroclinicity.

The wind deviations for California's N-LLJ shown in the hodograph (Fig. 14a) still have a clockwise rotation in 24 h. However, compared with the magnitude of the daily mean jet core wind, this diurnal cycle is not quite as obvious as the cycle for Quebec and Great Plain LLJs, but it is similar to the frequency cycle shown in Fig. 13d. In the comparison between geostrophic and ageostrophic winds (Fig. 14b and c), during the afternoon (15:00 and 18:00 LST), the amplitude of geostrophic wind is the largest, and the ageostrophic flow diminishes the geostrophic wind. However, in the morning, 12 h later, the relative angle between ageotrophic and geostrophic vectors does not change, meaning that the ageostrophic wind is still weakening the geostrophic wind and that there is no rotation of the ageostrophic wind, as Blackadar inertial oscillation theory describes. Figure 14d helps to explain the change in meridional winds. Looking at the magnitudes of ageostrophic winds, one can see that all are weak and southerly and that they do not exhibit a significant diurnal signal. Furthermore, the change in the geostrophic wind is highly consistent with the trend of the actual meridional wind. Thus, the N-LLJ in California can be considered mostly geostrophic, and the diurnal variation can be considered related to the change in geostrophic winds.

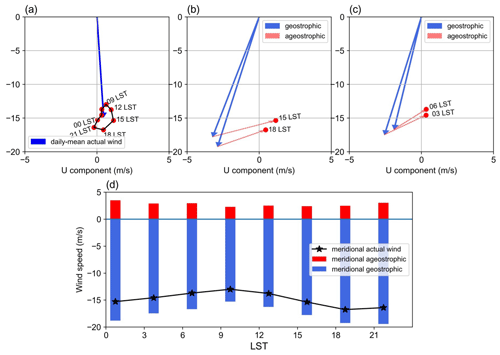
Figure 14 (a) Hodograph of jet core winds for the California coastal N-LLJ every 3 h over the whole JJA (red dots; solid line) and the daily averaged actual wind velocity (blue vector). Vectors of mean jet core geostrophic winds (solid blue) and ageostrophic winds (dashed red) at (b) 15:00/18:00 LST and (c) 03:00/06:00 LST. (d) Diurnal cycles of meridional components of actual (black line), geostrophic (blue bars), and ageostrophic winds (red bars).

5 Discussion and conclusion

This study applied a convection-permitting WRF model to conduct the analysis of LLJs in North America. The previous research for LLJs mainly focused on observation data, which have no fine coverage in temporal or spatial resolution. The studies using in situ observations may ignore some important features. Despite their better coverage, reanalysis datasets usually have a coarse spatial resolution and can introduce large inaccuracies in the identification of LLJs. In addition, the application of general numerical modeling cannot avoid the uncertainty caused by parameterizing small-scale physical processes. In contrast, high-resolution convection-permitting climate simulations can provide relatively more comprehensive descriptions of LLJs, especially for areas with complex geographic conditions or regions that lack soundings. Previous studies using high-resolution models conducted case analyses only of LLJs in a specific region (Aird et al., 2022). By expanding the target domain to the whole of North America and revealing the climatological characteristics of LLJs in different regions and scales, this paper provides an accurate reference for future research on LLJ-related processes in North America.

The convection-permitting WRF model is able to recapture some LLJs that have been previously studied, such as the Great Plain S-LLJ and the California coastal N-LLJ in the eastern Pacific Ocean, and has obtained relatively consistent results. The results indicate that the S-LLJ in the central US Great Plains is the most frequent and active in warm seasons and that three critical high-frequency centers occur in summer: the northeastern Mexico–Texas border, west–central Texas, and western Oklahoma to southern Kansas. This last result is consistent with the climatology generated by Doubler et al. (2015), using the NARR reanalysis data, but the patterns here are more representative of the topographic features in central and southern Texas. In addition, compared with the 40-year rawinsonde climatology in the central US by Walters et al. (2008), our study reveals that the S-LLJ frequency range of these three centers in the central US in summer is 25 %–30 %, which is slightly lower than the 35 % reported in the 2008 study. However, given the underestimated frequencies of 15 %–20 % in NARR climatology, there is an advantage of using high-resolution simulations in the vertical direction. Even though the simulation period does not match the time range of the literature exactly, the characteristics transcend specific time frames still offer a reference.

The convection-permitting simulation can also capture LLJs that were poorly detected previously using coarser resolution models and observational datasets. The winter N-LLJs over the eastern Rocky Mountains described in this paper are generally distributed over the central US from the Dakotas to Oklahoma with a low frequency (> 10 %) and over several sporadic small areas, with a high frequency (> 20 %) along the boundary of the Rockies. The main seasonal/diurnal variations identified in this study agree with those seen using rawinsonde data (Walters et al., 2008) and NARR reanalysis (Doubler et al., 2015). But the frequency of the LLJ occurrence over Nebraska–Kansas was underestimated in both convection-permitting simulations (∼ 10 %) and NARR (∼ 7 %), while high-frequency hot spots from Alberta to Colorado were not detected in either of the abovementioned studies, probably because measurements are lacking in these regions. The high-resolution simulation also detected LLJs, which researchers have hardly focused on. N-LLJs were detected near the eastern Quebec coast and in the Appalachian Mountains, as well as an S-LLJ over the British Columbia coast. In the work of Doubler et al. (2015), these LLJs were shown in the climatology patterns, but the 4 km WRF simulation offered more detailed descriptions of their locations. For example, this study found that the Appalachian N-LLJ extends from Georgia to the northwestern Atlantic, especially on summer nights (03:00–06:00 UTC), while NARR only captured LLJ occurrences over the middle coast of the Atlantic. The maximum frequency (7 %–10 %) detected in the NARR study is also less than what is illustrated here. As for the Quebec N-LLJ, the 4 km WRF revealed that it mostly occurs onshore near the coast with a frequency of over 25 % in winter, but NARR only provided a coarse occurrence distribution over northeastern Canada.

Based on the inertial oscillation theory (Blackadar, 1957) and the baroclinic theory near complex terrain (Holton, 1967), this paper also analyzed the background and formation mechanisms of three LLJs: the Great Plain S-LLJ, Quebec N-LLJ, and California coastal N-LLJ. Generally, all these LLJs are impacted by the thermodynamic circulations generated near their topography. The Great Plain S-LLJ is affected by slope heating, and the LLJs over Quebec and California are associated with the sea–land contrast. When the geostrophic and ageostrophic components of the LLJs are compared, results show that the inertial oscillation better explains the night enhancement of the Great Plains S-LLJ and that the diurnal feature of the Quebec N-LLJ is influenced by the combination of the Holton (1967) and Blackadar (1957) theories. As for the California coastal N-LLJ, no supergeostrophic state is found, making coastal baroclinicity variation a dominant factor for this LLJ's evolution the geostrophic wind changes.

This research adds to the existing knowledge of characteristics of the low-level wind maxima in North America, thus helping researchers obtain more reliable references about LLJs in this domain. Meanwhile, with the high-resolution features, it can provide more robust explanations for other interdisciplinary fields. The research also advances knowledge about the formation of three dominant LLJs. Although the 13-year simulation is likely too short to provide an ideal long-term climatic analysis, it is a less expensive option for finer numerical modeling in large domains. Additionally, we acknowledge certain limitations in the convection-permitting WRF simulation. While the vertical resolution in the boundary layer of this simulation is enhanced compared to other regional climate models (RCMs) or reanalysis datasets, it remains inferior to the observation density of radiosonde soundings. Consequently, the underestimation of LLJ events in this paper is expected, as noted in previous comparative analyses. Furthermore, numerical models inherently possess biases and uncertainties. Although employing the convection-permitting scale mitigates some uncertainties, it is important to recognize the limitations of these results. Additionally, the version of the input dataset used in this research is obsolete. However, with future advancements in technology, it is expected that longer and more accurate high-resolution simulations, as well as newer input data like ERA5, will become available. Future work will address the features and formation mechanisms of the small-scale, low-level wind maxima which have yet to be investigated.

Appendix A: Winter LLJs captured by ERA5 dataset

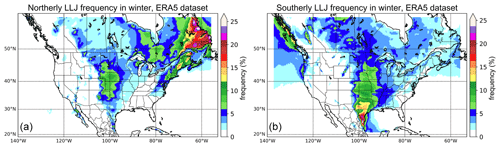
The convection-permitting WRF simulation exhibited excellent performance in investigating well-known LLJ systems, such as the California coastal N-LLJ and the Great Plains S-LLJ. Moreover, this appendix validates WRF-simulated significant winter jet systems over North America using the ERA5 reanalysis dataset. ERA5 is a global atmospheric reanalysis dataset produced by the European Centre for Medium-Range Weather Forecasts (ECMWF). It provides hourly data on a horizontal grid space of approximately 31 km, and the time range covers the period from 1940 till the present. ERA5 data are widely used in climate research, weather forecasting, and various applications that require high-quality atmospheric data.

The validation period is the same as the WRF simulation (2000–2013). From Fig. A1 below, it is evident that during winter, a greater number of significant N-LLJ systems in the North American continent are mostly concentrated in eastern Canada. In most parts of Newfoundland and southeastern Quebec, the occurrence frequency of N-LLJs exceeds 15 %, and the maximum can even surpass 25 %. However, in the WRF simulation (Fig. 3d), the model can only capture N-LLJs on the north bank of the Saint Lawrence River due to the northern boundary of the study domain overlapping with the Quebec border. In comparison, the WRF-simulated frequency of N-LLJs in southeastern Quebec essentially exceeds 25 %, overestimated by about 5 % compared to the ERA5 reanalysis. Additionally, it is worth noting that the N-LLJs along the downstream Rockies are also identified in the ERA5 dataset. The areas where the frequency exceeds 5 % are mainly distributed from Alberta to northern Texas, consistent with the findings in Sect. 3.2.1. Moreover, the high-value center (> 10 %) is located in central Kansas. In terms of the differences between the two datasets, the results of the WRF simulation match more geographical features and reveal scattered high-value spots (> 15 %) in some regions with special terrains (see Fig. 3d). Furthermore, the winter Great Plains S-LLJs in ERA5 reanalysis exhibit similar features, with frequencies ranging from around 15 % to 20 % in southern Texas. In summary, the WRF model can accurately capture the features of winter LLJ systems, which are validated by the ERA5 reanalysis dataset over northern America. Even though the frequency of LLJs occurrence is overestimated, the convection-permitting WRF simulation can provide detailed descriptions of LLJs near complex terrains.

Figure A1 Winter occurrence frequency of N-LLJs (a) and S-LLJs (b).