Ether and ester formation from peroxy radical recombination: a qualitative reaction channel analysis

The least volatile organic compounds participating in atmospheric new-particle formation are very likely accretion products from self- and cross-reactions of peroxy radicals (RO₂). It has long been assumed that the only possible accretion product channel in this reaction is that forming a peroxide (${\mathrm{RO}}_{\mathrm{2}}+{\mathrm{RO}}_{\mathrm{2}}\to \mathrm{ROOR}+{\mathrm{O}}_{\mathrm{2}}$), but it has recently been discovered that a rapid alkoxy radical (RO) decomposition may precede the accretion step of the mechanism, forming slightly fragmented but more stable ether (ROR) or ester (RC^′(O)OR) accretion products. In this work, the atmospheric implications of this new reaction channel have been explored further by using a modified version of the Generator for Explicit Chemistry and Kinetics of Organics in the Atmosphere (GECKO-A) software to generate a large amount of representative RO₂ + RO₂ reactive pairs formed from the oxidation of typical primary hydrocarbons and by applying structure–activity relationships (SARs) to predict the potential accretion products. These data are analysed in terms of the formation of low-volatility products, and new discoveries are presented on what types of RO₂ are especially efficient (and which are surprisingly inefficient) at forming accretion products. These findings are discussed in terms of the atmospheric relevance of these new RO₂ + RO₂ reaction channels. As the generation of these data rests on several simplifications and assumptions, many open questions worthy of later studies are also raised.

1 Introduction

1.1 Atmospheric background

The formation and growth of secondary organic aerosol (SOA) particles in pristine environments is dependent on the gas-phase formation of low-volatility organic molecules, but the exact formation pathways of such organics is only partially known (Kanakidou et al., 2005). The self- and cross-reactions of peroxy radicals (RO₂) are assumed to be important sources of such low-volatility molecules (Berndt et al., 2015), as this is one of the rare cases of gas-phase atmospheric reactions where accretion products, products with a larger carbon count than the reactant radicals, can form. The previously known accretion-product-forming pathway of these recombination reactions is a peroxide connecting the carbon skeletons of the reactant RO₂ in the reaction ${\mathrm{RO}}_{\mathrm{2}}+{\mathrm{RO}}_{\mathrm{2}}\to \mathrm{ROOR}+{\mathrm{O}}_{\mathrm{2}}$. This is, however, not the only possible product of this reaction, and we will therefore briefly review the history of studies on this reaction. The mechanism of RO₂ recombination has been known to go through an unstable tetroxide intermediate since the proposed Russell mechanism for its decomposition (Russell, 1957). However, the currently accepted mechanism for the reaction was presented by Ingold (1969), in which the tetroxide ejects an O₂ molecule, leaving behind a triplet-state bimolecular complex of two alkoxy radicals, ³(RO…OR):

$$\begin{array}{}\text{(R1)}& \begin{array}{rl}& {\mathrm{RO}}_{\mathrm{2}}+{\mathrm{RO}}_{\mathrm{2}}\leftrightarrow {\mathrm{RO}}_{\mathrm{4}}\mathrm{R}\\ & \to {}^{\mathrm{1}}\left(\mathrm{RO}\mathrm{\dots }{\mathrm{O}}_{\mathrm{2}}\mathrm{\dots }\mathrm{OR}\right)\to {}^{\mathrm{3}}\left(\mathrm{RO}\mathrm{\dots }\mathrm{OR}\right){+}^{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}.\end{array}\end{array}$$

Recent theoretical studies indicate that, in the case of CH₃O₂ + CH₃O₂ recombination, the ejection of one CH₃O radical from the (CH₃O…O₂…OCH₃) complex is thermodynamically (but not necessarily kinetically) favourable to that of O₂ (Salo et al., 2024). Recent experimental studies also suggest a novel in-complex $\left(\mathrm{RO}\mathrm{\dots }{\mathrm{O}}_{\mathrm{2}}\right)\to {\mathrm{R}}_{-\mathrm{H}}=\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}}$ reaction channel from the self-reaction of the HOC₂H₄O₂ radical (Murphy et al., 2023). Here, however, we will operate under the assumption that these reactions are only possible for very weakly bound systems and that channel (R1) is exclusively the fate of generic RO₂ + RO₂ reactions. In the mechanism proposed by Ingold (1969), the ³(RO…OR) complex has three further reaction channels: a dissociation pathway (Reaction R2) into two free alkoxy radicals (RO), an intermolecular H-shift (Reaction R3) forming an alcohol and a carbonyl, and an intersystem crossing (ISC) into the singlet state followed by barrierless recombination into a peroxide accretion product (Reaction R4, ROOR). The branching ratios for these three pathways have been studied both experimentally (Orlando and Tyndall, 2012) and computationally (Hasan, 2023). In our previous work (Peräkylä et al., 2023), we found an unexpected fourth reaction channel for an α-pinene-derived ³(C₁₀H₁₅O₂O…OC₁₀H₁₅O₂) complex, in which one of the alkoxy radicals undergoes a rapid β-scission reaction, thereby producing a C₁₉H₂₈O₅ ester accretion product. Assuming these kinds of reactions are possible for other systems as well, we may update the full mechanism of peroxy radical recombination to include the following four pathways:

$$\begin{array}{}\text{(R2)}& {\displaystyle }{}^{\mathrm{3}}\left(\mathrm{RO}\mathrm{\dots }\mathrm{OR}\right)\stackrel{\mathrm{Dissoc}}{⟶}\mathrm{RO}+\mathrm{RO}\text{(R3)}& {\displaystyle }\stackrel{\mathrm{H}-\mathrm{Shift}}{⟶}{\mathrm{R}}_{-\mathrm{H}}=\mathrm{O}+\mathrm{ROH}\text{(R4)}& {\displaystyle }\stackrel{\mathrm{ISC}}{⟶}\mathrm{ROOR}\text{(R5)}& {\displaystyle }\stackrel{\mathrm{RO}\mathrm{Dec}}{⟶}{\mathrm{ROR}}^{\prime }(+\mathrm{P}),\end{array}$$

where R^′ denotes that the original organic R group may be fragmented, in which case P is the second fragmentation product (CH₂O is the case of the previously mentioned C₁₉H₂₈O₅ ester product). The computational results provided by Peräkylä et al. (2023) suggest that the occurrence of channel (R5) depends on the unimolecular decomposition rate of the RO outspeeding reaction channels (R2), (R3), and (R4), on which we already have produced a body of computational work. The rate of the dissociation channel is primarily predicted by the binding energy of the ³(RO…OR) complex, ranging from 2⋅10¹ to $\mathrm{8}\cdot {\mathrm{10}}^{\mathrm{10}}{\mathrm{s}}^{-\mathrm{1}}$. (Franzon, 2023) Dissociation is therefore likely to be uncompetitive for larger, more functionalized, and thus more strongly binding pairs of RO. An equally unambiguous trend for the H-shift rate has proved difficult to determine (Hasan et al., 2023), but the computed H-shift rates show a weak negative correlation with the binding energy, suggesting that this pathway is also less competitive for larger and more functionalized radicals. These H-shift rates are rarely above 10⁹ s⁻¹. It is also notable that only primary and secondary RO can act as H donors, meaning that this channel does not exist at all if both of the reacting RO₂ are either acyl peroxy radicals (RC(O)O₂) or tertiary RO₂. The ISC rate seems to be systematically on the order of 10⁹ s⁻¹, with the ³(CH₃O…OCH₃) complex and some stereoisomers of ONO₂-substituted RO acting as outliers (Hasan, 2023). In summary, if reaction channels of type (R5) are of any significance, they must outspeed the ISC rate if the ³(RO…OR) is strongly binding and outspeed the dissociation and bimolecular H-shift rates if the complex is weakly binding. Based on the information above, it seems that the RO decay rate must be close to 10⁸ s⁻¹ to be of any importance and preferably above 10⁹ s⁻¹ to be a main channel.

The in-complex RO decomposition we observed (Peräkylä et al., 2023) was a β-scission reaction forming an acyl-centred radical combining with the other RO to form an ester. Similar reactions forming alkyl radicals as decomposition products will presumably result in ether accretion products. Decay rates of RO radicals inside complexes are currently unknown, but, as a first approximation, we may estimate them using the corresponding reaction rates of free RO. This is convenient, as the atmospheric reactions of alkoxy radicals have already been studied widely. The structure–activity relationship (SAR) by Vereecken and Peeters (2009) and Novelli et al. (2021) for β-scission reactions of free RO suggests that there are multiple chemical structures that reach the approximate threshold of 10⁸ s⁻¹, suggesting that this channel may be quite common. We also ought to entertain the possibility that β-scission reactions are not the only kind of unimolecular RO reaction which may occur in-complex. A review on the atmospheric chemistry of alkoxy radicals by Orlando et al. (2003) discussed three additional reaction classes for (non-halogenated) RO: unimolecular H-shifts, ester rearrangement, and O₂ addition. The ranges of known reaction rates for each of these are shown in Fig. 1. Upon closer examination, however, only the unimolecular H-shift pathway is reportedly fast enough to cross our importance threshold of 10⁸ s⁻¹ in some known cases, as the ester rearrangement and O₂ addition pathways are both limited to (pseudo-unimolecular in the latter case) rates of around 10⁵ s⁻¹. To avoid confusion between H-shift reactions of type (R3) and type (R5), we refer to the former as bimolecular H-shifts and the latter as unimolecular H-shifts.

In this work, we aim to explore the wider atmospheric significance of channel (R5) using an RO₂ + RO₂ accretion product generator code based on the Generator for Explicit Chemistry and Kinetics of Organics in the Atmosphere (GECKO-A; Aumont et al., 2005) software, which we call GECKO-AP (… of Organic Accretion Products). GECKO-AP makes use of all the RO₂ and RO chemistry already included in GECKO-A, combined with simple parametrizations of the knowledge we currently have of the competing reaction channels to generate datasets of all the possible peroxide, ether, and ester accretion products derived from a GECKO-A-generated set of RO₂. These datasets of accretion products are then analysed in order to learn which of these reactions are most important, especially when it comes to the formation of low-volatility products. The purpose of this article is not to determine accurate branching ratios for these channels, as this most likely requires both characterization of further ester or ether product from experiments and extensive computations benchmarked against such experiments. Instead, the purpose of this work is to inform future efforts on where to start looking and to assess general qualitative features of accretion products formed by the recently discovered pathways.

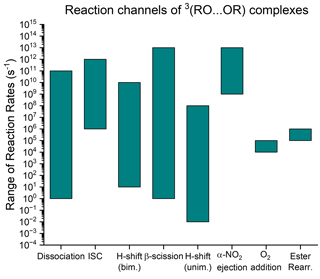
Figure 1 A visualization of the range of rates of the three known reaction channels of ³(RO…OR) complexes compared to the unimolecular reaction rates of free RO radicals considered in this work. The range of dissociation rates is from Franzon (2023), the ISC and bimolecular H-shifts are from Hasan (2023), the β-scission and unimolecular H-shift rates are from Vereecken and Peeters (2009) and Vereecken and Peeters (2010), and the O₂ addition and α-ester rearrangement are from Orlando et al. (2003). The α-NO₂ ejection is discussed in Sect. 2.1.4.

1.2 GECKO-A

In order to place the importance of Reaction (R5) in a wider atmospheric context, a large selection of atmospherically relevant peroxy radicals must be screened to determine the cases where these in-complex decomposition reactions are competitive. For this purpose, GECKO-A was used to generate large numbers of atmospherically relevant RO₂. As GECKO-A only generates the products from channels (R2) and (R3) for RO₂ recombination reactions according to the parametrization presented in Jenkin et al. (2019), a new code was written to generate all the possible accretion products (both channels R4 and R5) from each individual pair of RO₂. The structure of the code is described in detail in Sect. 2.1. Using this code, three large accretion product datasets from representative precursor molecules were produced, which are presented in Sect. 2.2 and analysed in detail in Sect. 3 to determine two things: what the existence of reaction channel (R5) implies for the formation of low-volatility products from RO₂ recombination and which aspects of this channel are worth studying in more detail.

The GECKO-A tool generates explicit atmospheric chemical mechanisms from a list of organic precursors provided as input. The chemistry included in the version of GECKO-A used to generate the data was VOC oxidation by OH (Jenkin et al., 2018a, b), alkene oxidation by O₃ (Jenkin et al., 2020), VOC oxidation by NO₃ (Kerdouci et al., 2014), photolysis for some select chromophores (Aumont et al., 2005), thermal decomposition of peroxy acyl nitrates (−C(O)OONO₂) (Jenkin et al., 2019), RO decomposition (Vereecken and Peeters, 2009), (mostly bimolecular) reactions of RO₂ (Jenkin et al., 2019), and stabilized Criegee intermediate chemistry (Newland et al., 2022). All generated molecules are grouped by generation based on the minimum number of stable closed-shell species that are produced in the formation of that molecule. For example, CH₂OHCH₂OOH and CH₂(ONO₂)CH₂OOH are first-generation products of ethene. The molecules produced from the oxidation of these (including the radicals) are second-generation products, and so on. The GECKO-A molecule generator creates all the oxidation pathways up to a specified generation n and above a specified critical saturation vapour pressure p_c (Aumont et al., 2005). In this study, the generated chemical mechanisms were used to provide lists of peroxy radicals expected to be representative of typical atmospheric RO₂ in their structure but also in their probability to be formed. GECKO-A also calculates a theoretical maximum yield of formation parameter y, which is used to filter out minor reaction channels in the mechanism generation. As the mechanism generation code makes minimal assumptions on environmental conditions such as relative humidity and bimolecular reactant (such as OH, O₃, NO₃, HO₂, NO, NO₂, and RO₂) concentrations, this parameter does not account for competition between different bimolecular reactions. The maximum yield is therefore “theoretical” in the sense that the y value of (for example) isoprene + NO₃ products corresponds to real yields in conditions where isoprene oxidation is completely dominated by NO₃. This means the y values have the disadvantage of occasionally over-representing products with high yields from slow reactions, but, from the perspective of our qualitative RO₂ + RO₂ reaction channel analysis, the environmental independence is an advantage, as it allows us to treat all hypothetically possible atmospheric RO₂ + RO₂ reactions uniformly without the loss of generality. The y values of the RO₂ generated by GECKO-A were thus used as a filter with which to select RO₂ + RO₂ pairs for further treatment. A comparison of theoretical maximum yields with simulated formation rates and concentrations is performed in Sect. S8.

2 Methods

2.1 Generation of accretion product datasets

As the scope of this work is limited to exploring the potential accretion products, the GECKO-AP code was built to simply generate a list of RO₂ + RO₂ accretion products from a list of RO₂ generated in the GECKO-A mechanism. In this section, the process of creating accretion product datasets from an RO₂ list is described in detail. As the potential number of pairings increases combinatorically with the length of the RO₂ list ($N+\frac{N\mathrm{!}}{\mathrm{2}\mathrm{!}(N-\mathrm{2})\mathrm{!}}=\frac{N^{\mathrm{2}}}{\mathrm{2}}+\frac{N}{\mathrm{2}}$), care was taken to efficiently filter out all of the least important radicals (Sect. 2.1.1), least probable RO₂ + RO₂ pairs (Sect. 2.1.2 and 2.1.3), and least competitive product channels (Sect. 2.1.5) in the code.

2.1.1 Filtering of individual RO₂

The list of RO₂ radicals generated in a GECKO-A mechanism was used as input for the GECKO-AP code, with some filtering done to reduce the number of products. Firstly, a yield cutoff y_c was chosen such that all RO₂ with theoretical maximum yield y<y_c were filtered out. Secondly, CH₃O₂ was systematically left out as a rule from these lists, as all of our previously studied ³(CH₃O…OR) systems have had rapid dissociation (Franzon, 2023) and bimolecular H-shift (Hasan et al., 2023) rates. We thus suspect that CH₃O₂ + RO₂ reactions are not a significant source of accretion products in the atmosphere and most certainly are not a source of large low-volatility accretion products. Thirdly, RC(O)O₂s with hydroperoxide (OOH) substituents was also excluded, as the rapid H-scrambling reaction into peracid-substituted alkyl peroxy radicals is expected to be effectively irreversible (Knap and Jørgensen, 2017). As GECKO-A currently lacks RO₂ H-shift and H-scrambling reactions, a simple exclusion of these radicals from partaking in RO₂ + RO₂ was seen as a suitable correction.

2.1.2 Filtering of RO₂ pairs by probability

Another method of filtering out the least important data is to only treat the RO₂ + RO₂ pairs above a certain probability threshold, which in the GECKO-AP code is formulated in terms of RO₂ + RO₂ reaction kinetics. The formation rate of a ³(RO…OR) complex is

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}\left[\right(\mathit{\alpha }\mathrm{\dots }\mathit{\beta }\left)\right]}{\mathrm{d}t}}=k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}}}\left[\mathit{\alpha }\right]\left[\mathit{\beta }\right].\end{array}$$

Here, [α] and [β] are the concentrations of the two reacting peroxy radicals, and $k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}}}$ is the recombination rate coefficient. Since the best estimation we have of individual RO₂ concentrations in the GECKO-A mechanism generator is the theoretical maximum yield y, we estimate an equivalent recombination yield using these:

$$\begin{array}{}\text{(2)}& y_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }\mathit{\beta }}=k_{\mathrm{rel}}{y}_{\mathit{\alpha }}{y}_{\mathit{\beta }},\end{array}$$

where y_α and y_β are the theoretical maximum yields of the RO₂ α and β. Since a yield must be between 0 and 1 by definition, the rate coefficient k_rel must also be expressed relative to some maximum, for which we use the RO₂ + RO₂ rate coefficient for the GECKO-A RO₂ class 8 (see Table 3): $k_{\mathrm{rel}}=\frac{k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}}}}{\mathrm{5.3}\cdot {\mathrm{10}}^{-\mathrm{12}}{\mathrm{cm}}^{\mathrm{3}}\mathrm{molec}{.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}}$. The RO₂ + RO₂ rate coefficient is determined using a slight simplification of the scheme described in the Supplement of Jenkin et al. (2019), where the individually calculated self-reaction rate coefficient is replaced by one of the nine GECKO-A RO₂ class rates (Table 1). This way, k_rel can efficiently be calculated for large numbers of RO₂ pairs without using up memory for self-reaction rates. As suggested by Jenkin et al. (2019), cross-reactions between RC(O)O₂ and other RO₂ are always treated as collision-limited, whereas other rates are determined using a geometric mean of the two self-reaction rates, with an additional factor of 2 for reactions between tertiary and primary or secondary RO₂ ($f_{\mathrm{t}+\mathrm{p},\mathrm{s}}$).

$$\begin{array}{}\text{(3a)}& {\displaystyle }{k}_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }\mathrm{9}}=\mathrm{1.1}\cdot {\mathrm{10}}^{-\mathrm{11}}{\mathrm{cm}}^{\mathrm{3}}\mathrm{molec}{.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}\text{(3b)}& {\displaystyle }{k}_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }\mathit{\beta }}=\mathrm{2}{f}_{\mathrm{t}+\mathrm{p},\mathrm{s}}\sqrt{k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }}\cdot k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\beta }}}\end{array}$$

Table 1 The nine RO₂ + RO₂ rate classes used in GECKO-A, adapted from Jenkin et al. (2019).

For reactions between RC(O)O₂ and other radicals, two additional correction factors are used to scale down the yields. Firstly, as GECKO-A lacks unimolecular H-shift (autoxidation) reactions for peroxy radicals, the recombination yields of RC(O)O₂ other than CH₃C(O)O₂ were scaled down based on a uniform autoxidation sink of 1 s⁻¹. Secondly, we must also consider that bimolecular reactions between RC(O)O₂ and common atmospheric inorganic radicals (OH, HO₂, NO_x) are generally faster than the corresponding reactions for alkyl RO₂, which means that the relationship between the faster recombination rates of RC(O)O₂ and the resulting recombination yields is not directly comparable. Thus, we apply a “rate-to-yield factor” of 0.56 to RO₂ + RO₂ reactions involving acyl peroxy radicals based on a quick derivation of the relationship between the rates and the yield. More details are given in Sect. S2. To summarize, we may rewrite Eq. (2) in the form used in the GECKO-AP code:

$$\begin{array}{}\text{(4)}& y_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }\mathit{\beta }}=f_{\mathrm{9}}{\displaystyle \frac{k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }\mathit{\beta }}}{k_{\mathrm{8}}}}{y}_{\mathit{\alpha }}{y}_{\mathit{\beta }},\end{array}$$

where k₈ is the RO₂ + RO₂ rate coefficient for rate class 8 and f₉ is the correction applied to RO₂+RC(O)O₂ reactions, which is 1 if neither α or β is RC(O)O₂, 0.56 if either is CH₃C(O)O₂, and 0.035 if either is some other RC(O)O₂ (see Supplement). To filter out less probable RO₂ pairs, a cutoff yield y_c is defined below which the RO₂ + RO₂ pair is not considered. The same value is used to filter out individual RO₂, as y_α<y_c directly implies y_αβ<y_c.

2.1.3 Filtering of RO₂ pairs with rapid dissociation

As we are primarily interested in the accretion-product-forming channels (R4) and (R5), it also makes sense to filter out RO₂ pairs for which the branching ratios of channels (R2) and (R3) can be presumed to be high. As experimental data on these branching ratios are still relatively scarce, we are not able to create reliable SAR calculators for the rates of channels (R2) and (R3), let alone branching ratios. However, the results from our previous computational studies (Franzon, 2023; Hasan, 2023) indicate that both of these rates are negatively correlated with the binding energy of the ³(RO…OR) complex. It has been suggested elsewhere (Peräkylä et al., 2023) that the ability of the RO to form intermolecular H-bonds is key to suppressing these two channels, especially channel (R2), and this might offer us a viable approach to filter out RO₂ pairs with weakly bound ³(RO…OR) complexes using only the information available to the mechanism generator. For this purpose, −OH, −OOH, −C(O)OH, and −C(O)OOH were treated as H-bond-donating groups, whereas −CHO, −C=O−, −C(O)OH, −C(O)OOH, −NO₂, −ONO₂, −OONO₂, −C(O)OONO₂, and the radical oxygen were treated as H-bond-accepting groups. In addition, every C–H bond (aliphatic or aromatic) was treated as a partial H-bond donor, as these may stabilize larger ³(RO…OR) complexes in the presence of H-bond acceptors, as noted in the Supplement of Peräkylä et al. (2023). Using these parameters, an effective H-bond number (HBN) was calculated for each pair of alkoxy radicals:

$$\begin{array}{}\text{(5)}& {\mathrm{HBN}}_{\mathit{\alpha },\mathit{\beta }}=n_{\mathrm{D},\mathit{\alpha }}\cdot n_{\mathrm{A},\mathit{\beta }}+n_{\mathrm{D},\mathit{\beta }}\cdot n_{\mathrm{A},\mathit{\alpha }},\end{array}$$

where D and A refer to donor and acceptor, respectively, and α and β refer to the two RO in the complex. Regarding the specific form of the equation, we emphasize that the purpose of the equation is to mimic the observed trends in ³(RO…OR) binding energies, which do not exclusively depend on the ability to form H-bonds but also on dipole–dipole bonds, dispersion interactions, and Pauli repulsion of the two radical oxygens. Out of these secondary interactions, the dipole–dipole bonding largely depends on the presence of the same functional groups as the H-bonding interactions, at least in the context of gas-phase organic chemistry. This means that we were able to obtain a good agreement (a correlation coefficient of ≈0.92) between the HBN_α,β value and the binding energies of ³(RO…OR) complexes presented by Hasan (2023) by adjusting the “partial H-bond donor” value assigned to each C–H bond. The optimal value chosen used in the code was 0.04. Based on the dissociation rates calculated using these binding energies (Franzon, 2023), an HBN cutoff of 1.75 was chosen, below which accretion products are not generated for that specific RO₂ pair. The full analysis of how this cutoff was chosen is described in Sect. S1.

2.1.4 In-complex RO reactions

For all RO₂ in the input list, a systematic search of decomposition reactions is performed for the corresponding RO. The approach for finding the reactions is very similar to that using the ordinary GECKO-A code (Aumont et al., 2005). As discussed in the Introduction, the following three reaction classes were judged to potentially be competitive in-complex:

1. β-scission, which turns the alkoxy moiety into a carbonyl and the site of the broken bond into an alkyl radical. The search is performed in a similar way to in the base GECKO-A code for free alkoxy radicals, relying mainly on the structure–activity relationship (SAR) of Vereecken and Peeters (Vereecken and Peeters, 2009; Novelli et al., 2021).

2. A unimolecular H-shift to the alkoxy oxygen resulting in the formation of an alkyl radical with one additional OH substituent. This relies mainly on the SAR of Vereecken and Peeters (Vereecken and Peeters, 2010).

3. α-NO₂ ejection, resulting in a carbonyl and an NO₂ radical. This reaction is set to an arbitrarily high ($k_{\mathit{\alpha }-{\mathrm{NO}}_{\mathrm{2}}}={\mathrm{10}}^{\mathrm{12}}{\mathrm{s}}^{-\mathrm{1}}$) rate in GECKO-A to conveniently get rid of these compounds. As this reaction happens to have interesting implications for accretion product formation (See Sect. 3.3), computational rate coefficients were calculated for a set of small representative compounds using the ORCA software (Neese, 2022). According to these calculations, the reaction will typically have rates closer to the $[{\mathrm{10}}^{\mathrm{9}},{\mathrm{10}}^{\mathrm{10}}{\mathrm{s}}^{-\mathrm{1}}]$ range, which is still highly competitive in-complex. Computational details are found in Sect. S3.

The rates of all reactions for each individual RO are compared, and all channels found to be competitive enough to at least be minor products (using a branching ratio cutoff of 0.05) next to an assumed universal ISC rate of 10⁹ s⁻¹ are considered for in-complex reaction branching ratio calculations.

For every reaction, the stability of the radical product is checked by running through a list of barrierless decomposition reactions. This was done utilizing a version of the code described in Sect. 3.1 of Aumont et al. (2005), with a shorter list of “immediate” reactions to account for what kind of reactions might actually occur inside the complex. The code starts by identifying if a radical is delocalized or not, and it implements the following list of reactions for either the non-delocalized radical or both Lewis structures of the delocalized radical. All three reactions are barrierless according to Vereecken et al. (2004) and Vereecken (2008).

• 1.

  $\mathrm{R}\mathrm{1}-\mathrm{C}\mathrm{•}\mathrm{OO}-\mathrm{R}\mathrm{2}\to \mathrm{R}\mathrm{1}-\mathrm{C}=\mathrm{O}+\mathrm{•}\mathrm{O}-\mathrm{R}\mathrm{2}$. Barrierless decomposition of peroxides at the radical centre.

• 2.

  $\mathrm{R}-\mathrm{C}\mathrm{•}\mathrm{OOH}\to \mathrm{R}-\mathrm{C}=\mathrm{O}+\mathrm{•}\mathrm{OH}$. Barrierless decomposition of α-hydroperoxy alkyl radicals into a carbonyl and an OH radical.

• 3.

  $\mathrm{R}-\mathrm{C}\mathrm{•}{\mathrm{ONO}}_{\mathrm{2}}\to \mathrm{R}-\mathrm{C}=\mathrm{O}+{\mathrm{NO}}_{\mathrm{2}}\mathrm{•}$. Barrierless decomposition of α-nitrate alkyl radicals into a carbonyl and a nitro radical.

These may not be the only further decomposition reactions that are possible for the product radicals of in-complex RO decomposition reactions. Low-barrier reactions, such as decomposition of acyl oxy radicals into alkyl radicals and carbon dioxide ($\mathrm{RC}\left(\mathrm{O}\right)\mathrm{O}\mathrm{•}\to \mathrm{R}\mathrm{•}+{\mathrm{CO}}_{\mathrm{2}}$; Vereecken and Peeters, 2009) and decomposition of diacyl radicals into an acyl radical and carbon monoxide ($\mathrm{R}-(\mathrm{C}=\mathrm{O})-\mathrm{C}\mathrm{•}=\mathrm{O}\to \mathrm{R}-\mathrm{C}\mathrm{•}=\mathrm{O}+\mathrm{CO}$; Méreau et al., 2001), were also considered but ultimately not included, as these reactions are not barrierless and may not occur after an endothermic (Orlando et al., 2003) RO decomposition. These downstream decomposition reactions must likely be barrierless to efficiently compete with the association of the radical product and the other RO in the ³(RO…OR) complex.

A separate output is written for all the RO reactions that are considered for in-complex branching to help keep track of the accretion products.

2.1.5 Filtering of accretion products

As discussed in Sect. 1.1, we currently assume that the RO decomposition reaction is generally followed by recombination of the two radicals into an ether or ester. In the Supplement of Peräkylä et al. (2023), this assumption was tested for a small model system, where it turned out that this recombination had a high-energy barrier in the triplet state and thus required an ISC. However, this ISC was faster than the ISC of the ³(RO…OR) complex, being on the order of 10¹¹ s⁻¹. While a fast dissociation of the two radicals post-RO decomposition cannot entirely be ruled out in reality, it is reasonable to assume that the dissociation of the product radical and the remaining RO is less competitive than the dissociation of the two RO in the ³(RO…OR) complex, especially as RO β-scission reactions are typically endothermic. The GECKO-AP code thus operates on the assumption that the RO decomposition always leads to recombination of the radical product with the second RO in the complex.

The final part of the code cycles through all pairs of RO₂ not filtered out by either the probability or the HBN criteria. Branching ratios for all available reaction routes are considered by comparing the reaction rates of both RO and the ISC rate, with the latter assumed to be 10⁹ s⁻¹ in all cases. Reaction routes are filtered by two criteria: (1) branching ratio and (2) final yield, which is a combination of recombination yield and branching ratio. Low branching ratios are filtered out using the branching ratio cutoff 0.05, with more tolerance for channels with higher rate uncertainty. The uncertainty factors f used were 1 for β-scissions, 5 for H-shifts, and 50 for spin-flips. The first two of these factors were chosen based on the reported uncertainties in the SARs for these reaction classes: a factor of 2 for the β-scissions (Vereecken and Peeters, 2009), and a factor of 10 for the fastest H-shifts (Vereecken and Peeters, 2010). The relative uncertainty of the ISC rates was determined from the variance in the available computational ISC rates for ³(RO…OR) rates (Hasan, 2023).

In other words, channels were filtered out if

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{k_r}{k_{\mathrm{ISC}}+{\sum }_i^{n_{\mathit{\alpha }}}{k}_i+{\sum }_j^{n_{\mathit{\beta }}}{k}_j}}<{\displaystyle \frac{\mathrm{0.05}}{f}},\end{array}$$

where n_X is the number of unimolecular reaction channels found for the RO X, whereas k_i and k_j are the rates of said channels. Note that the rates of channels (R2) and (R3) are neglected by necessity, as we lack a simple way to estimate them with the information available to the code. As a final criterion, Eqs. (2) and (6) are combined into a single inequality with an additional factor of 10:

$$\begin{array}{}\text{(7)}& y_{\mathrm{Prod}}={\displaystyle \frac{y_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}}}\times k_r}{k_{\mathrm{ISC}}+{\sum }_i^{n_{\mathrm{A}}}{k}_i+{\sum }_j^{n_{\mathrm{B}}}{k}_j}}<\mathrm{10}{y}_{\mathrm{c}}{\displaystyle \frac{\mathrm{0.05}}{f}},\end{array}$$

where y_c is the same cutoff used to filter RO₂ pairs by recombination probability. This value was adjusted between the three datasets, as seen in the next section. The role of the factor of 10 is to ensure that minor channels are more heavily filtered out for less likely pairs of RO₂. For the reaction channels that pass all filters, the molecular structure, the molecular mass, and the saturation vapour pressure are printed out in the output using two different group additivity methods, SIMPOL (Pankow and Asher, 2008) and Nannoolal (Nannoolal et al., 2004, 2008) (the latter with Compernolle's additional −OOH and −C(O)OOH parameters; Compernolle et al., 2010).

As an additional note on the Nannoolal vapour pressures, a previous computational study on the vapour pressures of large ROOR-type accretion products (Kurtén et al., 2016) suggested that the Nannoolal model produces strange results when applied to these molecules. A comparison was performed on the vapour pressures presented in that study with those predicted by the above implementation of the Nannoolal model (see Sect. S4). Based on this comparison, we conclude that the error is likely in the UManSysProp (Topping, 2015) implementation of Nannoolal utilized by Kurtén et al. (2016), not in the model itself.

2.2 Data generation and curation

2.2.1 Presentation of the datasets

Three datasets of accretion products with different precursor molecules were produced in order to analyse the most important trends in varying atmospheric conditions. For all runs, a critical vapour pressure value of $p_{\mathrm{c}}={\mathrm{10}}^{-\mathrm{13}}$ atm was used, meaning that further gas-phase chemistry was not generated for closed-shell molecules with p_Sat<p_c. The maximum generation of oxidation products and the cutoff value for $y_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}}}$ were adjusted for each run to ensure that the datasets were kept at a manageable size and that low-yield downstream products would not be overrepresented in the data. A sensitivity analysis of the y_c parameter is found in Sect. S5. These three datasets are presented below:

• 1.

  The DTA dataset, including the accretion products produced in the atmospheric oxidation of n-decane, toluene, and α-pinene. The oxidation products generated by GECKO-A for this set of precursor molecules have been studied in detail before (Isaacman-VanWertz and Aumont, 2021; Besel et al., 2023), so a dataset made out of oxidation products previously missing from GECKO-A is a good addition. Accretion products were generated up to the fourth generation, and the yield cutoff y_c=0.0045 was used.

• 2.

  The terpene dataset, including the accretion products produced in the atmospheric oxidation of isoprene, α-pinene, β-pinene, limonene, β-ocimene, sabinene, Δ-3-carene, and myrcene. These are the eight most common terpene molecules (Sindelarova et al., 2014). A dataset composed of all the RO₂ + RO₂ cross-products from these precursors should represent accretion product formation occurring in pristine low-NO_x forest environments reasonably well. Accretion products were generated up to the second generation, and the yield cutoff y_c=0.003 was used.

• 3.

  The caryophyllene dataset, including the accretion products from β-caryophyllene, a sesquiterpene for which aerosol particle formation has recently been studied (Dada et al., 2023). Here, products were only generated up to the first generation, as some of the second-generation accretion products proved unmanageably complex for the mechanism generator. The yield cutoff y_c=0.001 was used.

The isomer switching code presented by Valorso et al. (2011) was turned off during the runs to ensure the traceability of the RO₂ formation mechanisms. RO₂+OH reactions were also turned off when generating these datasets, as this leads to the formation of hydrotrioxides (ROOOH) in the current parametrization of GECKO-A. The chemistry of these molecules is not well-known, but, based on known decomposition and OH oxidation rate coefficients for CH₃OOOH and isoprene-derived ROOOH (Assaf et al., 2018; Anglada and Solé, 2018; Berndt et al., 2022), we are not able to completely neglect other OH or O₃ oxidation pathways of hydrotrioxides, both of which we lack systematic data for. Fortunately, with a typical atmospheric OH concentration of ${\mathrm{10}}^{\mathrm{6}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ (Wayne, 2000), the RO₂+OH channel will often be outcompeted by the other channels, so ignoring them is not a massive loss in chemical accuracy.

2.2.2 Dataset curation

Additional GECKO-A mechanisms without the GECKO-AP code were generated for each set of precursor molecules to supply the datasets with additional metadata. Six mechanisms were generated with a limited set of VOC oxidants (only OH, only O₃, only NO₃, OH + O₃, OH + NO₃, and O₃ + NO₃). Each RO₂ in the accretion product datasets was assigned a required combination of atmospheric oxidants based on the RO₂ list resulting from these mechanisms. Similarly, for the DTA and terpene datasets, a GECKO-A mechanism was generated for each product generation leading up to the final one to assign a generation to each of the RO₂ in the dataset. Finally, for each precursor molecule in the DTA and terpene datasets, a mechanism was generated with only one precursor in to label which of the precursors each of the RO₂ is derived from. Based on this RO₂ labelling, a final probability-based filtering criterion was applied to all datasets, as OH and NO₃ are known to rarely have simultaneously high concentrations: the former is produced by photolysis of O₃, while the latter is decomposed by photolysis (Seinfeld and Pandis, 2016). For this reason, the cross-reactions of OH-derived RO₂ and NO₃-derived RO₂, along with all their products, were removed from the data. Care was taken not to accidentally remove radicals produced from both oxidation mechanisms (for example, products of H-abstraction). By the same logic, RO₂ with formation mechanisms requiring OH oxidation of a VOC in one generation and NO₃ oxidation in the next (or vice versa) was also removed. Admittedly, these mechanisms are more plausible than cross-reactions of OH-derived RO₂ and NO₃-derived RO₂ if the lifetimes of the first-generation closed-shell products exceed the diurnal cycle; nevertheless, it is likely that the GECKO-A mechanism generator overestimates the yields of these radicals relative to all other RO₂.

For the purpose of data analysis, four versions of the final data were created for each dataset. The first contains all the reaction channels found by the code, including those removed by the OH + NO₃ criteria. These data are not analysed separately in this work, but they are distributed as a reference. In the second version of data, the OH + NO₃ products have been removed, but nothing else has. This version is analysed in Sect. 3.3. In the third version, all of the non-accretion products are removed (analysed in Sect. 3.4), and, in the fourth version, all the duplicate accretion products are removed. This last version is only used for the figures in Sects. 3.2 and S6, but the existence of such uniqueness-filtered datasets was regarded as useful for potential follow-up studies, such as the analysis performed by Besel et al. (2023) for the data presented by Isaacman-VanWertz and Aumont (2021).

2.3 Estimation of atmospheric concentrations

In order to explore the impact of accretion product formation from RO₂ + RO₂ reactions, RO₂ concentrations were calculated for representative conditions of biogenic environments where the RO₂ + RO₂ reactions are expected to be relatively important. RO₂ concentrations were calculated from the numerical solution of the kinetic steady-state equations (Eq. 8) based on the reactions in the GECKO-A mechanism. Furthermore, the mechanism was limited to isoprene oxidation and includes only the first- and second-generation radicals (7581 reactions). Firstly, however, a representative set of bimolecular reactant concentrations was chosen based on balancing a simpler set of steady-state equations, with only CH₄, CO, CH2_O, and CH₃OH present as organic precursors. The criteria used to find the ideal RO₂ + RO₂ conditions were based on the GEOS-Chem-modelled probability distributions presented by Kenagy et al. (2024), according to which a $\frac{k_{{\mathrm{RO}}_{\mathrm{2}}\mathrm{NO}}\left[\mathrm{NO}\right]}{k_{{\mathrm{RO}}_{\mathrm{2}}\mathrm{NO}}\left[\mathrm{NO}\right]+k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{HO}}_{\mathrm{2}}}\left[{\mathrm{HO}}_{\mathrm{2}}\right]}$ value of 0.2 corresponds to both an $\frac{\left[{\mathrm{RO}}_{\mathrm{2}}\right]}{\left[{\mathrm{HO}}_{\mathrm{2}}\right]}$ ratio well above 1 and a not-insignificant probability density. Assuming the RO₂+NO and RO₂+HO₂ rates are approximately similar for typical RO₂, we thus balanced the steady-state equations for OH, O₃, HO₂, NO, NO₂, and NO₃, aiming for a $\frac{\left[\mathrm{NO}\right]}{\left[\mathrm{NO}\right]+\left[{\mathrm{HO}}_{\mathrm{2}}\right]}$ ratio of 0.2.

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\mathrm{d}c}{\mathrm{d}t}}=\mathrm{sources}-\mathrm{sinks}\cdot c\approx \mathrm{0}\Rightarrow c\approx {\displaystyle \frac{\mathrm{sources}}{\mathrm{sinks}}}\end{array}$$

As the probability distribution of Kenagy et al. (2024) was weighted by isoprene + OH, it likely over-represents daytime conditions, as both isoprene and OH concentrations peak during the day (Wennberg et al., 2018). We thus re-balanced the steady-state equations with no photolysis reactions present, using the diurnal cycles presented by Bey et al. (1997) as reference. The resulting day- and nighttime concentrations of OH, O₃, HO₂, NO, NO₂, and NO₃ were treated as constants in the steady-state equations for the isoprene-RO₂. A (constant) isoprene concentration of ${\mathrm{10}}^{\mathrm{11}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ was used for daytime, and ${\mathrm{10}}^{\mathrm{10}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ was used for nighttime. The temperature T=298 K was used for both. Full details of how the steady-state equations were solved are found in Sect. S8.

3 Results and discussion

3.1 Competitive decomposition channels

Firstly, we use the β-scission and H-shift SARs (Vereecken and Peeters, 2009, 2010) to assess which of the reaction channels described in Sect. 2.1.4 are fast enough to occur in ³(RO…OR) complexes.

Assuming a constant ISC rate of 10⁹ s⁻¹, the β-scission rate must presumably be at least 10⁸ s⁻¹ in order for the product yield to be non-negligible. With Vereecken's suggested constant A-factor of $\mathrm{1.8}\cdot {\mathrm{10}}^{\mathrm{13}}{\mathrm{s}}^{-\mathrm{1}}$, an activation barrier below 30 kJ mol⁻¹ is needed to reach this rate at 298 K, which means 44.9 kJ mol⁻¹ worth of activating factors from the SAR's base value of 74.9 kJ mol⁻¹. The only activating factors to reach this barrier reduction single-handedly are the α-O group (present in all RC(O)O₂+RO₂ reactions), the β-NO group (not present in our data), and the opening of three- and four-membered rings (relevant for both pinenes, sabinene, and Δ-3-carene-derived RO₂). Other activating factors that are frequently present in our generated RO₂ are β$-\mathrm{C}=\mathrm{O}$ (leading to the formation of ester accretion products), β−OOH, β−OH, β$-\mathrm{C}=\mathrm{C}$, and the opening of five- and six-membered rings. In summary, there is no shortage of chemical structures present in atmospheric RO₂ that lead to competitive RO β-scission reactions. Interestingly, all of the most competitive β-scissions seem to be of the ring-opening type, which may partially explain why these reactions have eluded detection for so long. Exocyclic β-scissions have two products, whereas endocyclic scissions have one. Only the former is distinguishable from the ROOR in the mass spectrometric measurements which have thus far been the detection method of choice for highly oxidized organics in atmospheric chemistry (Ehn et al., 2014; Rissanen et al., 2014; Bianchi et al., 2019).

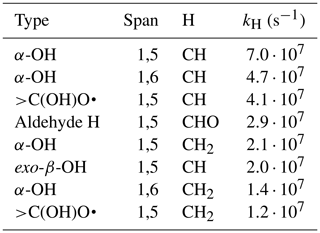
For the unimolecular H-shifts, the list of potentially competitive reactions is considerably shorter, as no H-shift has rates above 10⁸ s⁻¹ in the SAR. However, as these rates are uncertain by a factor of 10 (Vereecken and Peeters, 2010), the reactions with rates above 10⁷ s⁻¹ are still worth considering, especially as rates above 10⁸ s⁻¹ have been reported (Orlando et al., 2003). The unimolecular H-shift reactions above this rate threshold are listed in Table 2.

Table 2 A list of the RO unimolecular H-shifts which might be fast enough to occur in ³(RO…OR) complexes according to Vereecken's SAR (Vereecken and Peeters, 2010).

Overall, it is notable that the in-complex decomposition channels outnumber the ISC channels in the data: 142 009 to 79 833 in the DTA dataset and 161 784 to 129 585 in the terpene dataset. The ISC channels also have lower yields on average, accounting for only 22.1 % of the total yield of products from first-generation radicals in the DTA dataset and 35.4 % in the terpene dataset. These yields should be taken with a grain of salt, considering the large number of simplifications done when applying the filtering criteria, but they do offer some indication that these in-complex RO decomposition channels are common and become increasingly competitive with more complex RO intermediates.

3.2 Statistics on molecular properties

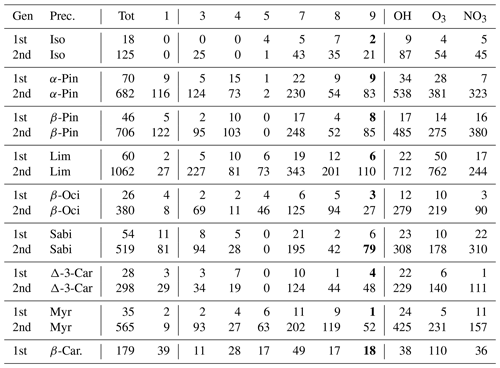
The distribution of RO₂ by rate classes are presented in Table 3 for the DTA dataset and in Table 4 for the terpene and β-caryophyllene datasets. One detail of note in the latter is that isoprene seems to almost exclusively generate RO₂ with fast RO₂ + RO₂ rates. This implies that isoprene-derived RO₂ contributes more than expected from its concentration when it comes to RO₂ recombination yields. Out of the seven monoterpenes treated in the data, limonene clearly produces the largest diversity of RO₂, owing to having both an endocyclic and an exocyclic C=C bond. We also see from both tables that the production of tert-RO₂ molecules is mostly dependent on the existence of tertiary double-bonded carbons, which is largely unsurprising.

Table 3 The number of peroxy radicals per generation, recombination rate class, and oxidant for each precursor molecule in the DTA dataset. For an explanation of the classes, refer to Table 1. The oxidant labels are defined inclusively (H-abstraction RO₂ with the label “OH, NO₃” is included in both columns). The class-9 number is bolded if it includes CH₃C(O)O₂.

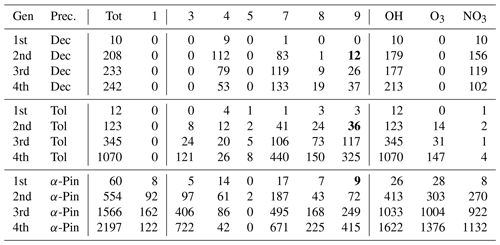
Table 4 The number of peroxy radicals per generation, recombination rate class, and oxidant for each precursor molecule in the terpene and β-caryophyllene datasets. For an explanation of the classes, refer to Table 1. The class-9 number is bolded if it includes CH₃C(O)O₂.

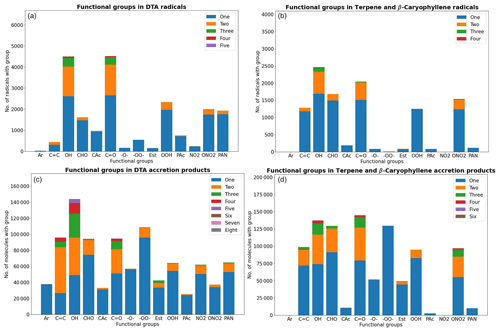
As atmospheric oxidation proceeds, the reactant RO₂ gets increasingly fragmented and oxidized. This is showcased for the radicals in the DTA dataset in Fig. 2 and for the terpene and β-caryophyllene datasets in Fig. 3. For the formed accretion products, the distribution of the same properties is presented in Figs. 4 and 5. As our methodology might be overemphasizing accretion products in later generations (see Sect. S5), all RO₂ are grouped by the generation where they first form, and all accretion products are labelled “Gen n+m”, where n and m are the generations of the two reacting RO₂. We also present histograms where each accretion product is weighted by our best proxy for the formation rate, which is the product of the RO₂ + RO₂ recombination rate (Eq. 3) and the in-complex branching ratio (Eq. 6). With this weighting, we neglect the relative importance of individual RO₂ radicals, as the theoretical maximum yields are not fully comparable. Comparing the branching-ratio-weighted carbon number distributions of accretion product and RO₂ in Fig. 5 to the corresponding radicals in Fig. 3, we notice an interesting trend in both the monoterpene and sesquiterpene results: the largest peak of accretion products occurs at C atom numbers only slightly larger than the bulk of the RO₂. In the terpene dataset, all of the major first-generation RO₂ have 10 C atoms, but the largest peak in accretion product yield is at 11 and 12 C atoms rather than 20. The same is seen in the β-caryophyllene dataset, where the RO₂ yield peaks at 13–15 C atoms, whereas the accretion product yield peaks at 14–17. However, the explanations for this phenomenon seem to differ between the two datasets. In the β-caryophyllene data, 73 % of this yield peak comes from cross-reactions of CH₃C(O)O₂ with the C_13–15 radicals; in the terpene dataset, this number is only 30 %. On the other hand, 38 % of this yield comes from fragmentations of larger RO₂ + RO₂ pairs, and the rest simply comes from recombinations of RO₂ with smaller C atom numbers. This underlines the importance of the RC(O)O₂ for accretion product formation, as they, at least in the Jenkin et al. (2019) parametrization, react rapidly even with the largest and most sterically hindered tert-RO₂.

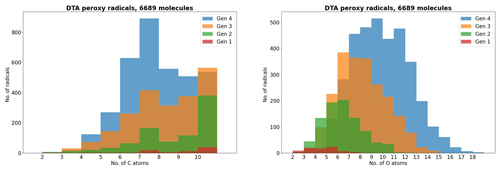
Figure 2 The peroxy radicals in the DTA dataset by number of C and O atoms, the latter including the two O atoms in the RO₂ functional group.

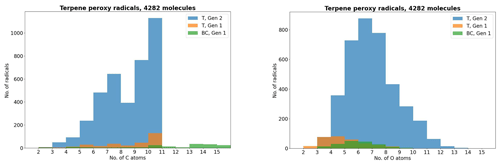
Figure 3 The peroxy radicals in the terpene (T) and β-caryophyllene (BC) datasets by number of C and O atoms, the latter including the two O atoms in the RO₂ functional group.

The distribution of functional groups in the RO₂ and (unique) accretion products is shown in Fig. 6. When comparing the two figures, we see that the number of accretion products with either ether or ester functionalities is less than those with a peroxide functionality, and this is only partially explained by the presence of peroxides in the DTA RO₂. This is likely due to the fact that there are more duplicates among the ether and ester products. The average in-complex branching ratio of all the ISC products remaining after filtering is 33.5 % in the DTA dataset and 36.6 % in the terpene dataset, again implying that the total yield of ether and ester products is typically higher. Interestingly, aromatic rings are highly represented in the DTA accretion products. The reason for this seems to be instrumental: the aromatic RO₂ in the data all have high yields due to being directly derived from the first H-abstraction product Ar–CH₂O₂, which has a yield of 100 % from NO₃ oxidation of toluene. Of course, H-abstraction from a methyl group by NO₃ is a slow reaction (Kerdouci et al., 2010), meaning that toluene + NO₃ might in reality not effectively be the dominant reaction even in favourable conditions. This detail is another example of why our results ought to be treated as qualitative rather than quantitative.

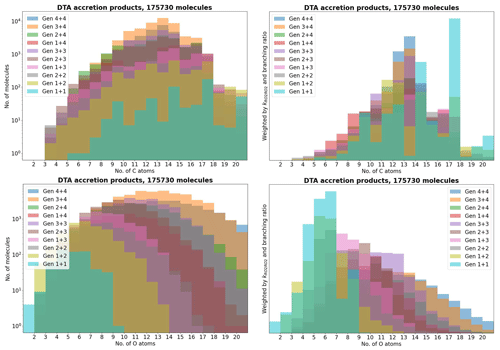
Figure 4 The accretion products in the decane, toluene, and α-pinene (DTA) dataset by number of C and O atoms.

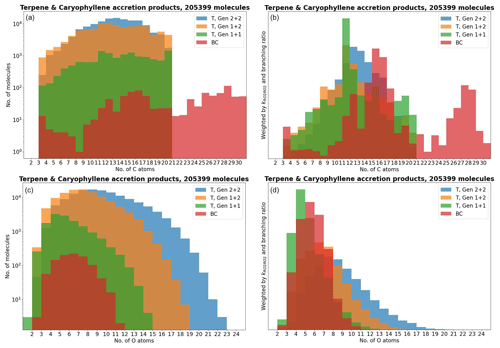
Figure 5 The accretion products in the terpene (T) and β-caryophyllene (BC) datasets by number of C and O atoms.

Figure 6 The distribution of functional groups in the DTA and terpene datasets for the RO₂ (a, b) and for the (unique) accretion products (c, d). CAc: carboxylic acid, C(O)OH. Est: ester, C(O)OC. PAc: peroxy acid, C(O)OOH. PAN: peroxy acyl nitrate, C(O)OONO₂.

3.3 Accretion-product-inhibiting reactions

Since we have presented a new channel for accretion product inhibition, namely the alkoxy radical decomposition reaction leading to ejection of either an OH or NO₂ radical, we should analyse the extent to which these inhibiting reactions occur in the data. This was done exclusively on the DTA dataset, due to the generally higher oxidation states of its RO₂ resulting in more competitive RO decompositions. The simplest type of inhibition reaction is the α-nitro ejection, which in the code ensures that peroxy radicals with an NO₂ group in the geminal position never form accretion products. As shown by our computational reaction rates in Sect. S3, this will not necessarily always be the case in reality, but the α-NO₂ ejection still ought to be among the most competitive channels. This is our first accretion-product-inhibiting reaction, and it can be treated as a given rule. The reaction is presented in the following scheme:

$$\begin{array}{}\text{(R6)}& \begin{array}{rl}& {\mathrm{R}}_{\mathrm{1}}\left({\mathrm{NO}}_{\mathrm{2}}\right){\mathrm{O}}_{\mathrm{2}}\mathrm{•}+{\mathrm{R}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\mathrm{•}\to \left({\mathrm{R}}_{\mathrm{1}}\right({\mathrm{NO}}_{\mathrm{2}}\left)\mathrm{O}\mathrm{•}\mathrm{\dots }\mathrm{•}{\mathrm{OR}}_{\mathrm{2}}\right)+{\mathrm{O}}_{\mathrm{2}}\\ & {\mathrm{R}}_{\mathrm{1}}\left({\mathrm{NO}}_{\mathrm{2}}\right)\mathrm{O}\mathrm{•}\to {\mathrm{R}}_{\mathrm{1}}=\mathrm{O}+\mathrm{•}{\mathrm{NO}}_{\mathrm{2}}\\ & ({\mathrm{R}}_{\mathrm{1}}=\mathrm{O}\mathrm{\dots }\mathrm{•}{\mathrm{NO}}_{\mathrm{2}}\mathrm{\dots }\mathrm{•}{\mathrm{OR}}_{\mathrm{2}})\to {\mathrm{R}}_{\mathrm{1}}=\mathrm{O}+{\mathrm{R}}_{\mathrm{2}}{\mathrm{ONO}}_{\mathrm{2}}.\end{array}\end{array}$$

These α-NO₂ radicals all form downstream from toluene oxidation pathways in the DTA dataset. The reaction channel responsible for these is NO₂ addition to aryloxy radicals ($\mathrm{Ar}-\mathrm{O}\mathrm{•}+{\mathrm{NO}}_{\mathrm{2}}\to \mathrm{Ar}(\mathrm{ortho}-{\mathrm{NO}}_{\mathrm{2}})\mathrm{OH}$; Platz et al., 1998); thus these peroxy radicals and the associated (RO…OR) complexes were left out from the following analysis.

The second reaction inhibiting the accretion product formation is the barrierless decomposition of α-hydroperoxy alkyl radicals, a reaction channel that is possible for all peroxy radicals with −OOH substituents. The inhibition is presented in the following scheme, in which R_OOH is a OOH-substituted carbon chain:

$$\begin{array}{}\text{(R7)}& \begin{array}{rl}& {\mathrm{R}}_{\mathrm{1}}{\mathrm{O}}_{\mathrm{2}}\mathrm{•}+{\mathrm{R}}_{\mathrm{OOH}}{\mathrm{O}}_{\mathrm{2}}\mathrm{•}\to \left({\mathrm{R}}_{\mathrm{1}}\mathrm{O}\mathrm{•}\mathrm{\dots }\mathrm{•}{\mathrm{OR}}_{\mathrm{OOH}}\right)+{\mathrm{O}}_{\mathrm{2}}\\ & {\mathrm{R}}_{\mathrm{OOH}}\mathrm{O}\mathrm{•}\to {\mathrm{R}}_{\mathrm{2}}\mathrm{•}\mathrm{OOH}\to {\mathrm{R}}_{\mathrm{2}}=\mathrm{O}+\mathrm{•}\mathrm{OH}\\ & ({\mathrm{R}}_{\mathrm{1}}\mathrm{O}\mathrm{•}\mathrm{\dots }\mathrm{•}\mathrm{OH}\mathrm{\dots }{\mathrm{R}}_{\mathrm{2}}=\mathrm{O})\to {\mathrm{R}}_{\mathrm{1}}\mathrm{OOH}+{\mathrm{R}}_{\mathrm{2}}=\mathrm{O},\end{array}\end{array}$$

where the reaction step R_OOHO•→R₂•OOH may be either a β-scission or a unimolecular H-shift. As a measure of the competitiveness of RO reactions leading to this inhibition channel, the average branching ratio as a function of the combined number of OOH groups in the RO₂ pair is shown in Fig. 7, both weighted and unweighted by the pair's recombination yield. As we see, the inhibition of accretion product formation increases significantly with the number of hydroperoxide groups.

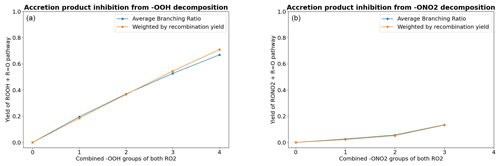
Figure 7 The impact of barrierless C•OOH and C•ONO₂ decomposition on the formation of accretion products. (a) The average branching ratio of RO reactions leading to C•OOH decomposition by the combined number of −OOH groups in the complex. (b) The same for RO reactions leading to C•ONO₂ decomposition. The results for n=4 are excluded because there was only one such RO₂ pair in the data.

Our third and final inhibition reaction is the barrierless decomposition of α-nitrate alkyl radicals, a very similar reaction to the corresponding −OOH reaction.

$$\begin{array}{}\text{(R8)}& \begin{array}{rl}& {\mathrm{R}}_{\mathrm{1}}{\mathrm{O}}_{\mathrm{2}}\mathrm{•}+{\mathrm{R}}_{{\mathrm{ONO}}_{\mathrm{2}}}{\mathrm{O}}_{\mathrm{2}}\mathrm{•}\to \left({\mathrm{R}}_{\mathrm{1}}\mathrm{O}\mathrm{•}\mathrm{\dots }\mathrm{•}{\mathrm{OR}}_{{\mathrm{ONO}}_{\mathrm{2}}}\right)+{\mathrm{O}}_{\mathrm{2}}\\ & -{\mathrm{R}}_{{\mathrm{ONO}}_{\mathrm{2}}}\mathrm{O}\mathrm{•}\to {\mathrm{R}}_{\mathrm{2}}\mathrm{•}{\mathrm{ONO}}_{\mathrm{2}}\to {\mathrm{R}}_{\mathrm{2}}=\mathrm{O}+\mathrm{•}{\mathrm{NO}}_{\mathrm{2}}\\ & ({\mathrm{R}}_{\mathrm{1}}\mathrm{O}\mathrm{•}\mathrm{\dots }\mathrm{•}{\mathrm{NO}}_{\mathrm{2}}\mathrm{\dots }{\mathrm{R}}_{\mathrm{2}}=\mathrm{O})\to {\mathrm{R}}_{\mathrm{1}}{\mathrm{ONO}}_{\mathrm{2}}+{\mathrm{R}}_{\mathrm{2}}=\mathrm{O}\end{array}\end{array}$$

The average branching ratio of these reactions is presented in Fig. 7.

As seen in Fig. 7, the hydroperoxide decomposition channel has a significantly higher inhibition yield compared to the nitrate decomposition channel. As most of the competitive alkoxy radical decomposition channels are β-scissions, the explanation for this observation can be found in the group contribution parameters in the β-scission SAR of Vereecken and Peeters (Vereecken and Peeters, 2009): if the alkoxy radical has a hydroperoxide group in the β-carbon, the activation energy is lowered by 38.9 kJ mol⁻¹. On the other hand, a nitrate group in the β-carbon only lowers the activation energy by 11.7 kJ mol⁻¹. Plugging this difference into an Arrhenius expression ($\exp \frac{\mathrm{27.2}\frac{\mathrm{kJ}}{\mathrm{mol}}}{RT}$) tells us that β-scission reactions leading to the formation of α-OOH alkyl radicals and to the ejection of an OH radical will typically be 10⁴ times faster than those leading to the ejection of an NO₂ radical; thus, they are more likely to be competitive. What this means in terms of atmospheric conditions is that highly ONO₂-substituted peroxy radicals forming in high-NO_x conditions have a slightly lower chance of forming organic accretion products from RO₂ recombination reactions compared to other sufficiently oxidized RO₂, while highly OOH-substituted peroxy radicals (for example, those forming in high HO₂ conditions) have an even lower chance. Even more importantly, peroxy radical autoxidation is also known to form products with multiple −OOH groups (Bianchi et al., 2019). Autoxidation reactions are currently missing from GECKO-A, so it is unclear how well the highly −OOH-substituted RO₂ in the data corresponds to those formed from autoxidation reactions. Considering the fact that the inhibition is primarily driven by fast β-scissions in the data, it is particularly notable that the optimal RO₂ H-shift span is 1,5 or 1,6 rather than 1,4 (Vereecken and Nozière, 2020). This suggest that −OOH groups originating from autoxidation may be less likely to be in β-position relative to the alkoxy carbon. For autoxidation-derived RO₂, the inhibition yield may thus increase less steeply compared to Fig. 7.

3.4 Analysis of vapour pressure distributions

As our main interest for accretion products comes from the formation of large low-volatility organic molecules, it is a worthwhile exercise to analyse the vapour pressure distribution of the predicted products. However, as the amount of data produced is rather large, this section will only discuss and visualize the observed main trends. Sections S6 and S7 feature more figures and tables on the vapour pressure distribution of the products. In addition to grouping the products by generation of radicals, they are also grouped by reaction channel, precursor molecule, and required VOC oxidants (OH, O₃, and NO₃) to better identify which reaction channels lead to the lowest-volatility products.

3.4.1 Distribution by reaction channel

The vapour pressure distribution of all the accretion products in the DTA and terpene datasets categorized by reaction channel is presented in Fig. 8. A few interesting trends pop up when viewing the data this way. Firstly, the vapour pressure distribution of the exocyclic β-scission products is shifted towards higher p_Sat values relative to the ISC products. This makes sense, as these products are more fragmented than their ROOR counterparts. This adds an interesting element to the suggestion by Peräkylä et al. (2023) that the ether and ester accretion products contribute more to aerosol particle growth thanks to their higher (thermal) stability. This increased stability often comes at the price of increased volatility, especially if the radical product of the β-scission is relatively small. In other words, these reactions may not always contribute more to aerosol particle growth compared to the ROOR product. On the other hand, the vapour pressure distribution of the endocyclic β-scission products is shifted towards lower p_Sat values, meaning that the same trade-off between stability and (low) volatility is not present. The reason for this is somewhat obvious: endocyclic β-scissions do not fragment the molecule. The same is true of the unimolecular H-shift products (which in theory ought to be even less volatile, as the reaction gives the product an additional OH group), but these products are less common due to the lower reaction rates (at least in the SAR). As seen when comparing the results between the three datasets, the different molecular structures present do not have a massive impact on the noted differences between the reaction types, but the ratio of exocyclic and endocyclic β-scissions obviously depends on the ring structures and positions of C=C bonds in the precursor VOC.

Figure 8 A bubble plot of the p_Sat distribution of all accretion products categorized by reaction channel for (a) the DTA dataset and (b) the terpene dataset. p_Sat is expressed in atm.

3.4.2 Distribution by precursor molecule

If endocyclic β-scissions are indeed the key to forming low-volatility ether and ester products, then the next question is which chemical structures present in the data are especially efficient at forming endocyclic RO₂ in high yields. This is, however, not the only important factor when it comes to the formation of accretion products, as endocyclic RO₂ tends to be on the lower end of the scale in terms of self-reaction rates, as it is by definition either secondary or tertiary RO₂ (see Table 1). Thus, simultaneously producing large amounts of rapidly reacting RC(O)O₂ or primary RO₂ with activating groups may also enhance accretion product formation from the endocyclic RO₂, as the cross-reactions between these will be faster than the self-reactions of the endocyclic RO₂.

Figure 9 shows the early-generation accretion products from the DTA and terpene datasets categorized by precursor molecule, including only RO₂ + RO₂ pairs where both radicals are produced by the same precursor molecule. From the DTA data, we see rather unsurprisingly that α-pinene and toluene are large sources of low-volatility accretion products, whereas n-decane is not. In the terpene results, we see that the lowest-volatility bins ($p_{\mathrm{Sat}}<{\mathrm{10}}^{-\mathrm{13}}$ atm) are dominated by β-pinene and sabinene, for less obvious reasons. Out of the 132 β-pinene-derived first-generation accretion products in these volatility bins, over half (68) were endocyclic β-scission channels. In all of these channels, the radical undergoing the decomposition is one of seven individual endocyclic RO combined with different pairs in the ³(RO…OR) complex. Recognizable from these seven were three OH- and ONO₂-addition-derived radicals each: one with both rings intact and two with only the four-ring intact. The seventh endocyclic RO is the VHP dissociation product of the C₉ Criegee intermediate from β-pinene ozonolysis. That these 7 (out of 52 non-filtered first-generation RO₂ radicals) dominate the low-volatility accretion products is another example of the key role endocyclic β-scissions play in low-volatility accretion product formation. For sabinene, another interesting trend emerges: only 40 out of the 100 $p_{\mathrm{Sat}}<{\mathrm{10}}^{-\mathrm{13}}$ atm accretion products are endocyclic β-scission products. There are 46 ISC products and 10 H-shift products. Upon closer examination, all four of the radicals undergoing the H-shift are primary RO in which sabinene's five-carbon ring has already been broken. In the H-shift classification of Vereecken and Peeters (2010), these reactions are either secondary α-OH or tertiary β-exo-oxo shifts. None of these are major products, as the SAR never predicts H-shift rates above 10⁸ s⁻¹, but these are nevertheless good examples of systems where the unimolecular H-shifts could be a competitive route to accretion product formation.

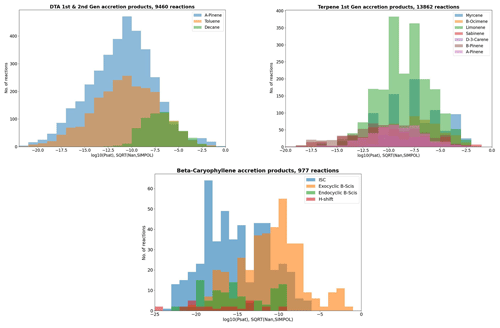
Figure 9 p_Sat distributions of the early-generation accretion products in each dataset categorized by precursor molecule.

Another point worthy of discussion is the detail raised in Sect. 3.2 that isoprene-derived RO₂ (iso-RO₂) typically has high RO₂ + RO₂ reaction rates. This implies that cross-reactions between iso-RO₂ with the larger but less abundant monoterpene-derived RO₂ (mono-RO₂) might be atmospherically significant. In Fig. 10, we see that the p_Sat values of these iso-RO₂ + mono-RO₂ products are not quite as low as those of mono-RO₂ + mono-RO₂, but a significant number of them stretch below the 10⁻¹³ atm threshold nevertheless. We should also note that, as our filtering method is based on relative product yields rather than product concentrations, we are likely underestimating the atmospheric occurrence of iso-RO₂ + mono-RO₂ pairs relative to mono-RO₂ + mono-RO₂ pairs, as global isoprene emissions outnumber total monoterpene emissions 3-fold in terms of concentration according to Sindelarova et al. (2014) (6-fold in terms of mass in the original source), which, roughly estimated, means a 20-fold higher formation rate on average relative to the individual monoterpenes in the dataset. We thus suspect that iso-RO₂ + mono-RO₂ reactions are an atmospherically significant but understudied pathway to the formation of $p_{\mathrm{Sat}}<{\mathrm{10}}^{-\mathrm{9}}$ atm contributing to aerosol particle growth, despite being experimentally less important than mono-RO₂ + mono-RO₂ for new particle formation according to Dada et al. (2023).

The results for β-caryophyllene are comparable to those of monoterpenes, as seen in Fig. 9c. However, we do see that the vapour pressure gap between the RO-fragmenting exocyclic β-scissions and the non-fragmenting endocyclic β-scission, H-shift, and ISC products is even wider, a fact which is largely explained by the closed-shell products of the exocyclic β-scissions also being larger. What this tells us is that formation of ELVOCs from sesquiterpenes is likely not qualitatively different from ELVOC formation from monoterpenes. Even with larger molecular sizes, the ELVOC formation is probably still dominated by the handful of reaction channels that produce the fastest oxidation without too much fragmentation.

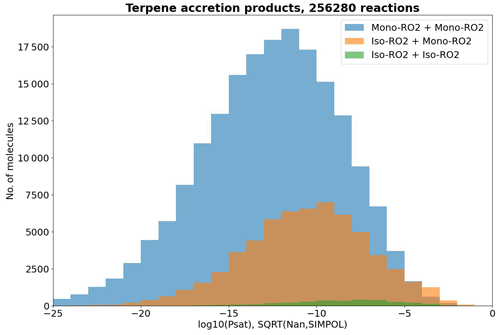
Figure 10 p_Sat distributions of the accretion products in the terpene dataset categorized by type of RO₂ pair. CH₃C(O)O₂-including pairs were separated from the rest due to their abundance and relatively high volatilities and due to CH₃C(O)O₂ being formed from all precursors in the dataset.

One interesting detail to consider is to which extent the use of SAR reaction rates and lack of RO₂ autoxidation misrepresents these trends. For the former, a recent computational study of β-scission rates in NO₃-derived monoterpene (Draper et al., 2024) RO provides an interesting point of comparison. For β-pinene in particular, the computational ring-opening activation energies are considerably higher than in the SAR, partially due to stereoelectronic effects arising from the orientation of the exocyclic ONO₂ group and partially due to steric repulsion from the four-carbon ring preventing the scission of the C–C bond connected to it. In terms of reaction rates, it seems that none of the SAR-predicted competitive ($k_{\mathit{\beta }}>{\mathrm{10}}^{\mathrm{8}}{\mathrm{s}}^{-\mathrm{1}}$) endocyclic β-scissions of limonene, β-pinene, and Δ-3-carene are competitive anymore once one accounts for these new stereochemical effects. This underlines the limitations of the SAR models when dealing with especially complex molecules. On the impact of the missing autoxidation reactions, the importance of endocyclic RO₂ makes it especially notable that GECKO-A lacks most unimolecular RO₂ ring closure reactions, which adds competitive routes for forming endocyclic RO₂. The only such reaction included in the current version is the bicyclic RO₂ formation known from OH oxidation of aromatics (first reaction in Table 14 of Jenkin et al., 2019). However, the work of Vereecken et al. (2021) shows that these reactions produce both endocyclic and exocyclic RO₂, of which the latter channel is more competitive in most cases. Nevertheless, the net increase in ring structures likely leads to the formation of endocyclic RO₂ in the next generation with some probability. We might also compare our emphasis on endocyclic RO₂ formation to the established consensus on monoterpene oxidation. According to Lee et al. (2023), it is the exocyclic RO₂ formed after the opening of the four-carbon ring in α- and β-pinene that contributes the most to the formation of low-volatility organics, at least among the OH-oxidation products. While this seems to be in conflict with our findings at first glance, we note that this contribution is due to a rapid H-shift reaction which leads to the formation of a (delocalized) endocyclic alkyl radical that may form two RO₂ (Fig. 11) (Møller et al., 2020). Furthermore, applying the SAR to the corresponding RO leads to an endocyclic β-scission rate of $\mathrm{2}\cdot {\mathrm{10}}^{\mathrm{10}}{\mathrm{s}}^{-\mathrm{1}}$ in both cases. In other words, the formation of low-volatility organics from this reaction channel is also likely driven by in-complex endocyclic β-scissions, and the lack of RO₂ autoxidation in GECKO-A only means that we are missing some of the reactions forming the most oxidized endocyclic RO₂.

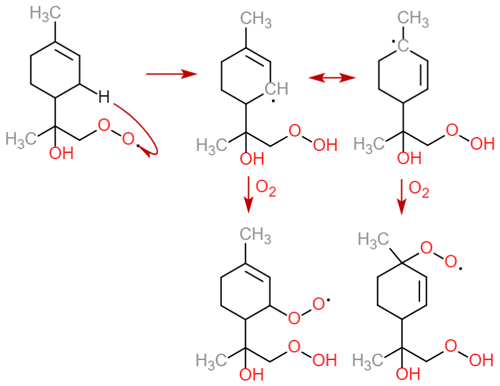
Figure 11 An autoxidation scheme for α-pinene-derived endocyclic RO₂ with rapid RO β-scission rates, adapted from Møller et al. (2020).

3.5 Atmospheric concentrations

The steady-state equations resulted in a total RO₂ concentration of $\mathrm{3.70}\cdot {\mathrm{10}}^{\mathrm{9}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ in the daytime and $\mathrm{1.26}\cdot {\mathrm{10}}^{\mathrm{9}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ in the nighttime. The daytime HO₂ concentration was $\mathrm{6.7}\cdot {\mathrm{10}}^{\mathrm{8}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$, which means that our $\frac{{\mathrm{RO}}_{\mathrm{2}}}{\left[{\mathrm{HO}}_{\mathrm{2}}\right]}$ ratio is within the Kenagy et al. (2024) probability distribution we were aiming for. In Table 5, we see how the high RO₂ concentration translated to reactivities (Eq. 9a, i.e. the fraction of RO₂ reacting with other RO₂) for different kinds of RO₂. CH₃O₂ reactivities are also presented, as all of these reactions were neglected in the GECKO-AP code. In Eq. (9a), α is the Jenkin rate class of the RO₂ the quantity is calculated for. Once again, we see a strong contrast between the classes of RO₂ with fast RO₂ + RO₂ rates and classes with slow RO₂ + RO₂ rates in the Jenkin et al. (2019) parametrization. RC(O)O₂ and β-substituted primary RO₂ react primarily with other RO₂ in sufficiently low-NO_x conditions, whereas secondary and especially tertiary RO₂ reacts primarily with inorganic radicals. We also see greatly elevated RO₂ reactivities at night due to lower concentrations of RO₂ scavengers NO, HO₂, and (to a lesser extent) OH. This suggests that accretion product formation from RO₂ + RO₂ reactions might be more important in the nighttime, all else being equal. The important caveat here is that all else is not equal in real diurnal cycles, in part due to generally lower RO₂ production with lower biogenic emission rates. Box-modelling studies will have to be performed to determine which effect is dominant. Another interesting detail is that CH₃O₂ was only responsible for a small fraction of the RO₂ reactivity, despite CH₃O₂ being known as the major atmospheric peroxy radical (Wayne, 2000). This may be explained by the fact that CH₃O₂ has no primary source besides CH₄+OH, for which the rate coefficient is over 4 orders of magnitude slower than that of isoprene + OH (Seinfeld and Pandis, 2016), which makes isoprene oxidation the far bigger source of RO₂ in these relative concentrations. This is a very promising result for the importance of the accretion product formation studied in this work, but it should be noted that the isoprene concentrations used here are only representative of environments close to emission sources, due to the short atmospheric lifetime (Wennberg et al., 2018). CH₃O₂ is thus more likely to dominate RO₂ + RO₂ reactions in environments far away from both alkene emission sources.

$$\begin{array}{}\text{(9a)}& {\displaystyle }\begin{array}{rl}& {\mathrm{RO}}_{\mathrm{2}}\mathrm{R}.\left(\mathit{\alpha }\right)\equiv \\ & {\displaystyle \frac{{\sum }_{\mathit{\beta }}^{\mathrm{9}}{k}_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }+\mathit{\beta }}\left[{{\mathrm{RO}}_{\mathrm{2}}}_{\mathit{\beta }}\right]}{{\sum }_j^{\mathrm{5}}{k}_{{{\mathrm{RO}}_{\mathrm{2}}\mathrm{Ox}}_j}\left[{\mathrm{Ox}}_j\right]+{\sum }_{\mathit{\beta }}^{\mathrm{9}}{k}_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }+\mathit{\beta }}\left[{{\mathrm{RO}}_{\mathrm{2}}}_{\mathit{\beta }}\right]}}\end{array}\text{(9b)}& {\displaystyle }\begin{array}{rl}& {\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\mathrm{R}.\left(\mathit{\alpha }\right)\equiv \\ & {\displaystyle \frac{k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }+\mathrm{6}}\left[{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\right]}{{\sum }_j^{\mathrm{5}}{k}_{{{\mathrm{RO}}_{\mathrm{2}}\mathrm{Ox}}_j}\left[{\mathrm{Ox}}_j\right]+{\sum }_{\mathit{\beta }}^{\mathrm{9}}{k}_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }+\mathit{\beta }}\left[{{\mathrm{RO}}_{\mathrm{2}}}_{\mathit{\beta }}\right]}}\end{array}\end{array}$$

Table 5 Concentrations and RO₂ and CH₃O₂ reactivities by RO₂ type in the steady-state solution.

The estimated RO₂ concentrations can further be used to estimate accretion product formation rates for the isoprene-derived products in the terpene dataset, through $k_{{\mathrm{RO}}_{\mathrm{2}}{\mathrm{RO}}_{\mathrm{2}},\mathit{\alpha }\mathit{\beta }}\left[\mathit{\alpha }\right]\left[\mathit{\beta }\right]\cdot \frac{k_r}{k_{\mathrm{ISC}}+{\sum }_i^{n_{\mathit{\alpha }}}{k}_i+{\sum }_j^{n_{\mathit{\beta }}}{k}_j}$, by combining the concentrations with Eqs. (4) and (6). This results in a total daytime formation rate of $\mathrm{3.84}\cdot {\mathrm{10}}^{\mathrm{6}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$ and a nighttime formation rate of $\mathrm{1.24}\cdot {\mathrm{10}}^{\mathrm{4}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$ for ROOR-type accretion products, whereas, for our RO-decomposition-derived ether- and ester-type accretion products, the daytime formation rate is $\mathrm{9.47}\cdot {\mathrm{10}}^{\mathrm{6}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$ and the nighttime rate is $\mathrm{1.96}\cdot {\mathrm{10}}^{\mathrm{4}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$. Since the latter reactions include an additional fragmentation step, it is worth noting that a majority of the formed ethers and esters (5.37⋅10⁶ and $\mathrm{1.78}\cdot {\mathrm{10}}^{\mathrm{4}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$ in the day and night, respectively) have more than isoprene's five carbon atoms. We expect the observed difference between daytime and nighttime rates to be mostly isoprene-specific, due to the exceptionally fast OH addition rate and due to the faster recombination rates of the most important daytime isoprene-RO₂. The fact that Jenkin's SAR for RO₂ self-reactions lacks activation parameters for nitrate groups (Jenkin et al., 2019) may also play a role in the underestimation of important nighttime radicals. The latter daytime value is almost 20 % of the product formation rate from RO₂+HO₂, assuming an upper-limit rate coefficient of $\mathrm{2}\cdot {\mathrm{10}}^{-\mathrm{11}}{\mathrm{cm}}^{\mathrm{3}}\mathrm{molec}{.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ and the daytime concentrations mentioned above, suggesting that these ether and ester accretion products are an important part of RO₂ chemistry in low-NO_x, high-VOC environments. More analysis of the results can be found in Sect. S8.

4 Conclusions

In our previous work (Peräkylä et al., 2023), we observed that rapid decomposition of alkoxy radicals in the ³(RO…OR) intermediates of peroxy radical recombination reactions may form ether and ester accretion products in addition to the already-known peroxides. In this work, we looked at a wider range of rapid alkoxy radical decomposition reactions to explore the full atmospheric implications of this new observed channel. While our quantitative data rest on a mountain of assumptions concerning the rates of the competing channels, we can already discern several qualitatively reliable trends:

• Our previously observed in-complex alkoxy radical decomposition was a β-scission reaction. By systematically looking at all the known reactions of free alkoxy radicals, we have concluded that the β-scission is often the most important in-complex RO decomposition channel.

• Furthermore, the most competitive β-scission reactions are endocyclic β-scissions, which produce products of the same mass as the known ROOR peroxide product. These were likely produced in many previous experiments but eluded identification due to the use of mass spectrometric detection methods.

• The products of exocyclic β-scission reactions typically have higher vapour pressures than the corresponding ROOR, which is to be expected, as they are smaller molecules. However, as these are ethers or esters rather than peroxides, they will be more stable towards both photochemical and thermal decomposition, as well as fragmenting oxidation, and thus more likely to contribute to SOA formation and growth.

• Unimolecular alkoxy radical H-shift reactions are rarely competitive with the β-scissions, but their products typically have lower vapour pressures than any other peroxy radical recombination products. These reactions might be very important for SOA formation from a small specific subset of peroxy radical recombinations.

• Acyl peroxy radicals are especially interesting for accretion product formation from peroxy radial recombination due to their ability to readily react with large tert-RO₂ with otherwise slow RO₂ + RO₂ rates.

• It has recently been postulated that the branching ratio of accretion-product-forming channels of peroxy radical recombination will progressively increase with RO₂ size and oxidation state (Hasan, 2023). This may not always be the case thanks to alkoxy decomposition reactions, where the products are a closed-shell organic molecule and a small inorganic radical. These reactions grow increasingly likely as the number of hydroperoxide, nitrate, and nitro groups in the reactant peroxy radicals increases.