Single-scattering properties of ellipsoidal dust aerosols constrained by measured dust shape distributions

Most global aerosol models approximate dust as spherical particles, whereas most remote sensing retrieval algorithms approximate dust as spheroidal particles with a shape distribution that conflicts with measurements. These inconsistent and inaccurate shape assumptions generate biases in dust single-scattering properties. Here, we obtain dust single-scattering properties by approximating dust as triaxial ellipsoidal particles with observationally constrained shape distributions. We find that, relative to the ellipsoidal dust optics obtained here, the spherical dust optics used in most aerosol models underestimate dust single-scattering albedo, mass extinction efficiency, and asymmetry parameter for almost all dust sizes in both the shortwave and longwave spectra. We further find that the ellipsoidal dust optics are in substantially better agreement with observations of the scattering matrix and linear depolarization ratio than the spheroidal dust optics used in most retrieval algorithms. However, relative to observations, the ellipsoidal dust optics overestimate the lidar ratio by underestimating the backscattering intensity by a factor of ∼2. This occurs largely because the computational method used to simulate ellipsoidal dust optics (i.e., the improved geometric optics method) underestimates the backscattering intensity by a factor of ∼2 relative to other computational methods (e.g., the physical geometric optics method). We conclude that the ellipsoidal dust optics with observationally constrained shape distributions can help improve global aerosol models and possibly remote sensing retrieval algorithms that do not use the backscattering signal.

1 Introduction

Desert dust aerosols are a key atmospheric component (Mahowald et al., 2014; Kok et al., 2021a, b; Adebiyi et al., 2023). Dust impacts the Earth system by modifying the radiation budget (Ito et al., 2021; Kok et al., 2023), hydrological cycle (Miller et al., 2004, 2006), cloud microphysics (Kiselev et al., 2017), and ocean biogeochemistry (Yu et al., 2015; Ito et al., 2019). Furthermore, dust impacts anthropogenic activities by degrading air quality and visibility (Mahowald et al., 2007; Huang et al., 2019) and harming human health (Giannadaki et al., 2014). To accurately estimate these dust impacts, global aerosol models and retrieval algorithms of passive and active remote sensing products need accurate dust single-scattering properties (Dubovik et al., 2006; Winker et al., 2007; Ansmann et al., 2012; Gliß et al., 2021).

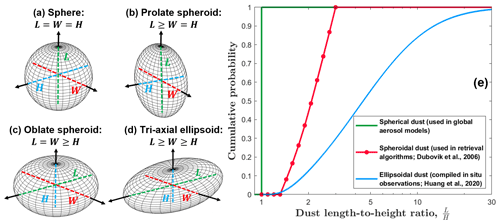
Figure 1 Global aerosol models and remote sensing retrieval algorithms use inconsistent and inaccurate dust shape quantifications. Most aerosol models approximate dust as (a) spherical particles, whose three perpendicular axes (i.e., dust length L, width W, and height H) are equal (Gliß et al., 2021). Most retrieval algorithms approximate dust as spheroidal particles with an equal presence of (b) prolate spheroid and (c) oblate spheroid at the same length-to-height ratio (Dubovik et al., 2006). A compilation of dust shape measurements found that the three perpendicular axes differ substantially for most dust particles and thus that approximating dust as triaxial ellipsoids (d) is more realistic (Huang et al., 2020). Panel (e) compares the cumulative probability distributions of the dust length-to-height ratio used in most aerosol models (in green) and retrieval algorithms (in red) and those obtained from a measurement compilation (in blue; see Sect. 2.2). The red dots in panel (e) denote the 13 shape bins used in the AERONET retrieval algorithm (Dubovik et al., 2006; Giles et al., 2019). AERONET chose its dust shape distribution as the one that resulted in the best fit between the simulated scattering matrix and laboratory-measured scattering matrix of a sample of crushed feldspar rocks (see Sect. 2.3). However, this shape distribution conflicts with measurements of dust shape and is substantially less aspherical than natural dust aerosols. This optimized dust shape distribution is widely adopted in most other retrieval algorithms (e.g., MODIS Deep Blue; Hsu et al., 2019). As such, aerosol models and retrieval algorithms substantially underestimate the dust length-to-height ratio relative to observations.

Dust single-scattering properties highly depend on dust shape (Bi et al., 2009, 2010; Lindqvist et al., 2014; Nousianien and Kandler, 2015; Saito et al., 2021; Saito and Yang, 2021; Kong et al., 2022), but global aerosol models and remote sensing retrieval algorithms use inconsistent and inaccurate dust shape quantifications (Fig. 1). Specifically, almost all global aerosol models approximate dust as spherical particles (Fig. 1a; Gliß et al., 2021), whereas most retrieval algorithms approximate dust as spheroidal particles (Fig. 1b and c) and use the length-to-height ratio to quantify dust asphericity (Dubovik et al., 2006; Hsu et al., 2019). By assuming a spherical or spheroidal dust shape, aerosol models and retrieval algorithms equate at least two of three dust perpendicular axes. However, a recent study that compiled dozens of in situ measurements of dust shape worldwide found that the three perpendicular axes differ substantially for most dust particles and thus that the triaxial ellipsoidal shape assumption (Fig. 1d) is more realistic for dust aerosols (Huang et al., 2020). In addition, relative to the compiled observations, aerosol models and retrieval algorithms substantially underestimate dust asphericity (Fig. 1e). These problematic dust shape assumptions of aerosol models and retrieval algorithms generate biases in dust single-scattering properties that further propagate into the estimated dust impacts.

To facilitate accounting for more realistic dust shape in aerosol models and retrieval algorithms, here we obtain dust single-scattering properties by approximating dust as triaxial ellipsoidal particles with observationally constrained shape distributions (Sect. 2). In Sect. 2, we then compare the obtained ellipsoidal dust optics with the spherical dust optics used in most aerosol models and the spheroidal dust optics used in most retrieval algorithms; these three optics simulations are validated against laboratory and field observations of dust optics. In Sect. 3, our results show that the ellipsoidal dust optics agree with observations substantially better than the spherical and spheroidal dust optics. Thus, the ellipsoidal dust optics with observationally constrained shape distributions can help improve aerosol models and retrieval algorithms.

2 Methods

This section presents our methodology for obtaining and evaluating the single-scattering properties of triaxial ellipsoidal dust aerosols constrained by measured dust shape distributions. In Sect. 2.1, we first introduce the definitions of single-scattering properties used in global aerosol models and remote sensing retrieval algorithms. Then, in Sect. 2.2, we obtain the single-scattering properties of ellipsoidal dust ensembles accounting for observational constraints on dust shape. In Sect. 2.3, we introduce the laboratory and field observations used as the ground truth to evaluate our obtained ellipsoidal dust optics. This section also introduces the spherical and spheroidal dust optics used in most aerosol models and retrieval algorithms. By comparing the spherical, spheroidal, and ellipsoidal dust optics against observations, we can test our hypothesis that ellipsoidal dust optics constrained by measured dust shape distributions are more realistic than the spherical and spheroidal dust optics.

2.1 Definitions of single-scattering properties

Single-scattering properties quantify how aerosols modify incident light after one instance of elastic scattering (Liou, 2002). Remote sensing retrieval algorithms and global aerosol models retrieve dust distributions and estimate dust impacts using seven key single-scattering properties, namely phase function, asymmetry factor, extinction efficiency, mass extinction efficiency, single-scattering albedo, linear depolarization ratio, and lidar ratio. We present the definitions of these single-scattering properties in detail below.

The modification of the incident light by aerosol scattering is quantified by the scattering cross section and the scattering matrix. The scattering cross section C_sca (m²) quantifies the total amount of light scattered by the aerosol particle. The 4×4 scattering matrix P_4×4 (unitless; also referred to as the Mueller matrix or the phase matrix) quantifies the angular modification of light by aerosol scattering (Liou, 2002; Mishchenko and Yurkin, 2017). Specifically, for an incident light beam (with intensity I_i, linear polarization components Q_i and U_i, and circular polarization component V_i), the scattered light beam (with intensity I_s, linear polarization components Q_s and U_s, and circular polarization component V_s) after one single-scattering event with a randomly oriented aerosol particle is as follows (Liou, 2002):

$$\begin{array}{}\text{(1)}& \left[\begin{array}{l}{I}_{\mathrm{s}}\\ Q_{\mathrm{s}}\\ U_{\mathrm{s}}\\ V_{\mathrm{s}}\end{array}\right]={\displaystyle \frac{C_{\mathrm{sca}}}{\mathrm{4}\mathit{\pi }{s}^{\mathrm{2}}}}\left[\begin{array}{llll}{P}_{\mathrm{11}}& P_{\mathrm{12}}& \mathrm{0}& \mathrm{0}\\ P_{\mathrm{12}}& P_{\mathrm{22}}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& P_{\mathrm{33}}& P_{\mathrm{34}}\\ \mathrm{0}& \mathrm{0}& -P_{\mathrm{34}}& P_{\mathrm{44}}\end{array}\right]\left[\begin{array}{l}{I}_{\mathrm{i}}\\ Q_{\mathrm{i}}\\ U_{\mathrm{i}}\\ V_{\mathrm{i}}\end{array}\right],\end{array}$$

where s (m) is the distance between the light detector and the scatterer (i.e., the aerosol particle), and the 4×4 scattering matrix P_4×4 has six non-zero independent elements for randomly oriented aerosols (Mishchenko et al., 2002; Hovenier et al., 2004; Mishchenko and Yurkin, 2017). Among the six independent elements, the so-called phase function P₁₁(θ) describes the angular change in light intensity, and the other five elements describe the angular change in light polarization. The phase function is normalized such that P₁₁ integrated against the scattering angle θ, and the azimuth angle ϕ yields 4π, as follows (Liou, 2002):

$$\begin{array}{}\text{(2)}& \underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}{P}_{\mathrm{11}}\left(\mathit{\theta }\right)\sin \left(\mathit{\theta }\right)\mathrm{d}\mathit{\theta }\mathrm{d}\mathit{\varphi }=\mathrm{4}\mathit{\pi }.\end{array}$$

The phase function is used in remote sensing retrieval algorithms to account for the angular distribution of aerosol-scattered radiation, whereas global aerosol models instead use the asymmetry factor to minimize computational costs. The asymmetry factor g (unitless) is as follows:

$$\begin{array}{}\text{(3)}& g={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}{P}_{\mathrm{11}}\sin \left(\mathit{\theta }\right)\cos \left(\mathit{\theta }\right)\mathrm{d}\mathit{\theta },\end{array}$$

where g is in between −1 and 1, g=0 when the radiation is scattered isotropically, and g increases (decreases) with the increasing amount of light scattered into the forward (backward) hemisphere within 0^∘ $<\mathit{\theta }<\mathrm{90}$^∘ (90^∘ $<\mathit{\theta }<\mathrm{180}$^∘; Liou, 2002). The other five elements of the scattering matrix quantify how the intensity and polarization of the outgoing light beam depends on the scattering angle and the polarization of the incoming light beam. Specifically, $-\frac{P_{\mathrm{12}}\left(\mathit{\theta }\right)}{P_{\mathrm{11}}\left(\mathit{\theta }\right)}$ quantifies the degree of linear polarization of the scattered light for the unpolarized component of the incident light, $\mathrm{1}-\frac{P_{\mathrm{22}}\left(\mathit{\theta }\right)}{P_{\mathrm{11}}\left(\mathit{\theta }\right)}$ quantifies the depolarization of the scattered light for the linear polarized component of the incident light, and P₃₃(θ), P₃₄(θ), and P₄₄(θ) quantify the modification on the circular polarization components by aerosol scattering (Liou, 2002; Nousiainen and Kandler, 2015; Mishchenko and Yurkin, 2017). These circular polarization components are rarely used in the current generation of remote sensing products. Active remote sensing products (e.g., airborne and ground-based lidars) widely use the linear depolarization ratio δ (unitless) to distinguish dust aerosols from the other aerosol types. δ quantifies the depolarization of the backscattered light for the linear polarized component of the incident light as follows (Mishchenko and Hovenier, 1995; Winker et al., 2007; Ansmann et al., 2012; Nousiainen and Kandler, 2015):

$$\begin{array}{}\text{(4)}& \mathit{\delta }={\displaystyle \frac{P_{\mathrm{11}}\left(\mathit{\pi }\right)-P_{\mathrm{22}}\left(\mathit{\pi }\right)}{P_{\mathrm{11}}\left(\mathit{\pi }\right)+P_{\mathrm{22}}\left(\mathit{\pi }\right)}}.\end{array}$$

In addition to aerosol scattering, aerosols can also modify the incident light by aerosol absorption, with the sum of scattering and absorption equalling the light extinction by aerosols. In analogy to the scattering cross section, the absorption and extinction cross sections C_abs (m²) and C_ext (m²), respectively, quantify the total amount of light absorbed and extinguished by the aerosol particle. These three cross sections depend on the physical size of the aerosol particle as follows:

$$\begin{array}{}\text{(5)}& C_{\mathrm{sca}/\mathrm{abs}/\mathrm{ext}}=Q_{\mathrm{sca}/\mathrm{abs}/\mathrm{ext}}\cdot A,\end{array}$$

where Q_sca, Q_abs, and Q_ext (unitless) are, respectively, the scattering, absorption, and extinction efficiencies that quantify a particle's ability to scatter, absorb, and extinguish light relative to its projected surface area A (m²; Liou, 2002). In addition to the extinction efficiency, global aerosol models use the mass extinction efficiency MEE (m² kg⁻¹) to quantify the light extinguished by aerosols per unit mass loading as follows (Kok et al., 2017):

$$\begin{array}{}\text{(6)}& \text{MEE}=Q_{\mathrm{ext}}\cdot {\displaystyle \frac{A}{M}},\end{array}$$

where M is the mass of the aerosol particle (kg). To quantify the contribution of light scattering to light extinction by aerosols, global aerosol models use the single-scattering albedo SSA (unitless) as follows:

$$\begin{array}{}\text{(7)}& \text{SSA}={\displaystyle \frac{C_{\mathrm{sca}}}{C_{\mathrm{ext}}}},\end{array}$$

which is in between 0 and 1 (Liou, 2002). Finally, remote sensing products widely use the lidar ratio S (sr) to quantify the ratio of extinct light to backscattered light (Liou, 2002; Dubovik et al., 2006; Nousiainen and Kandler, 2015), which is defined as follows:

$$\begin{array}{}\text{(8)}& S={\displaystyle \frac{\mathrm{4}\mathit{\pi }}{\text{SSA}\cdot P_{\mathrm{11}}\left(\mathit{\pi }\right)}}.\end{array}$$

These seven key single-scattering properties depend on dust microphysical properties, including dust shape, size, and mineralogy composition. A range of studies have investigated the impacts of biases in dust size and refractive index on dust single-scattering properties (e.g., Formenti et al., 2011; Kok et al., 2017; Di Biagio et al., 2017, 2019, 2020; Swet et al., 2020; Klose et al., 2021; Li et al., 2021, 2022; Meng et al., 2022; González-Flórez et al., 2022), but fewer studies have focused on the impact of bias in dust shape. The studies that did consider dust asphericity (e.g., Dubovik et al., 2006; Colarco et al., 2014) used dust shape approximations that deviate from observations (Fig. 1) to obtain dust single-scattering properties. To help quantify the biases in dust single-scattering properties due to dust shape, we account for the observational constraints on dust shape in obtaining dust single-scattering properties (Sect. 2.2).

2.2 Ellipsoidal dust optics with observationally constrained shape distributions

In this section, we first introduce two shape descriptors and their probability distributions from measurement compilation. We use these two probability distributions to quantify the asphericity of dust aerosols, approximating dust as triaxial ellipsoidal particles. Second, we introduce an extensive database containing shape-resolved single-scattering properties of ellipsoidal dust aerosols. Finally, we obtain the single-scattering properties of ellipsoidal dust ensembles by combining the shape-resolved single-scattering properties database with the two probability distributions of dust shape.

Dozens of in situ measurements across the world have used the length-to-width ratio ($\text{LWR}=\frac{L}{W}$; see Fig. 1) and the height-to-width ratio ($\text{HWR}=\frac{H}{W}$; see Fig. 1) to determine the shape of hundreds of thousands of individual dust particles. These measurements were compiled by Huang et al. (2020) and showed that both HWR and the deviation of LWR from unity (i.e., LWR−1) follow a lognormal distribution, as follows (e.g., Okada et al., 2001; Reid et al., 2003; Kandler et al., 2007, 2009, 2011; Sakai et al., 2010):

$$\begin{array}{}\text{(9)}& {\displaystyle }\begin{array}{rl}f\left(\text{LWR}\right)& ={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}\mathit{\pi }}\cdot \left(\text{LWR}-\mathrm{1}\right)\cdot {\mathit{\sigma }}_{\mathrm{L}}}}\\ & \exp \left[-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\displaystyle \frac{\ln \left(\text{LWR}-\mathrm{1}\right)-\ln \left(\stackrel{\mathrm{‾}}{{\mathit{\epsilon }}_{\mathrm{L}}}-\mathrm{1}\right)}{{\mathit{\sigma }}_{\mathrm{L}}}}\right)}^{\mathrm{2}}\right],\end{array}\text{(10)}& {\displaystyle }f\left(\text{HWR}\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}\mathit{\pi }}\cdot \text{HWR}\cdot {\mathit{\sigma }}_{\mathrm{H}}}}\exp \left[-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\displaystyle \frac{\ln \left(\text{HWR}\right)-\ln \left(\stackrel{\mathrm{‾}}{{\mathit{\epsilon }}_{\mathrm{H}}}\right)}{{\mathit{\sigma }}_{\mathrm{H}}}}\right)}^{\mathrm{2}}\right],\end{array}$$

where $\stackrel{\mathrm{‾}}{{\mathit{\epsilon }}_{\mathrm{L}}}$ and $\stackrel{\mathrm{‾}}{{\mathit{\epsilon }}_{\mathrm{H}}}$ are, respectively, the medians of LWR and HWR, and σ_L and σ_H are, respectively, the geometric standard deviations of LWR−1 and HWR. In addition, Huang et al. (2020) found that both LWR and HWR are insensitive to dust particle diameter and that the regional differences in LWR and HWR are modest. In the present study, we thus take $\stackrel{\mathrm{‾}}{{\mathit{\epsilon }}_{\mathrm{L}}}=\mathrm{1.70}\pm \mathrm{0.03}$, $\stackrel{\mathrm{‾}}{{\mathit{\epsilon }}_{\mathrm{H}}}=\mathrm{0.40}\pm \mathrm{0.07}$, ${\mathit{\sigma }}_{\mathrm{L}}=\mathrm{0.70}\pm \mathrm{0.02}$, and ${\mathit{\sigma }}_{\mathrm{H}}=\mathrm{0.73}\pm \mathrm{0.09}$, after the global averages compiled by Huang et al. (2020). Using these two globally representative shape distributions, we approximate dust as triaxial ellipsoidal particles with smooth surfaces and neglect the smaller-scale surface texture (such as sharp corners and surface roughness; Kalashnikova and Sokolik, 2004; Kemppinen et al., 2015; Saito et al., 2021; Saito and Yang, 2021; see Sect. 4.3 for a discussion of the impacts of these simplifications).

We seek to combine the two globally representative dust shape distributions (Eqs. 9 and 10) with an extensive database containing single-scattering properties of ellipsoidal dust aerosols (Meng et al., 2010). This database combined four computational methods to compute the single-scattering properties. The Lorenz–Mie theory was used for spherical particles with a size parameter x of 0.025–1000, the T matrix method was used for particles with x of 0.025–40, the discrete dipole approximation was used for x of 0.025–40, and the improved geometric optics method was used for x of 10–1000 (see Table 2 of Meng et al., 2010). At overlapping size parameters, results from different methods were averaged. These four methods together cover the size parameter range from Rayleigh to the geometric optics regimes. This extensive database contains the extinction efficiency $Q_{\mathrm{ext}}\left(n,k,x,\text{LWR},\text{HWR}\right)$, the single-scattering albedo $\text{SSA}\left(n,k,x,\text{LWR},\text{HWR}\right)$, the asymmetry factor $g\left(n,k,x,\text{LWR},\text{HWR}\right)$, and the six independent elements of the 4×4 scattering matrix $P_{\mathrm{4}\times \mathrm{4}}\left(n,k,x,\text{LWR},\text{HWR},\mathit{\theta }\right)$. These precalculated optics are resolved by the real (n) and imaginary (k) parts of dust refractive index, the size parameter (x), the length-to-width ratio and height-to-width ratio of the ellipsoidal dust particle (LWR and HWR), and the scattering angle (θ). We direct interested readers to Tables 1 and 2 of Meng et al. (2010) for the ranges of n, k, x, LWR, and HWR of the database.

We combined the shape-resolved optics database (Meng et al., 2010) with the two globally representative probability distributions of dust shape (Eqs. 9 and 10) to obtain the single-scattering properties of ensembles of ellipsoidal dust particles. That is, at a given dust volume-equivalent diameter, the obtained optics are ensemble averages of the single-scattering properties of 121 particle shapes (i.e., 11 values of LWR and 11 values of HWR; Meng et al., 2010); the weighting factor assigned to each particle shape, f_w(LWR,HWR), was determined by the two lognormal distributions of LWR and HWR (Eqs. 9 and 10). As such, at a given dust refractive index (n and k), light wavelength (λ), and dust volume-equivalent diameter (D), we obtain the extinction efficiency, mass extinction efficiency, single-scattering albedo, asymmetry factor, scattering matrix, linear depolarization ratio, and lidar ratio of ellipsoidal dust ensembles as follows (Liou, 2002; Grainger, 2022):

$$\begin{array}{}\text{(11)}& {\displaystyle }{\widehat{Q}}_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D\right)={\displaystyle \frac{\mathrm{4}}{\mathit{\pi }{D}^{\mathrm{2}}}}{\widehat{\mathit{\beta }}}_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D\right),\text{(12)}& {\displaystyle }\widehat{\text{MEE}}\left(n,k,\mathit{\lambda },D\right)={\widehat{Q}}_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D\right)\cdot {\displaystyle \frac{\mathrm{3}}{\mathrm{2}\mathit{\rho }D}},\text{(13)}& {\displaystyle }\widehat{\text{SSA}}\left(n,k,\mathit{\lambda },D\right)={\displaystyle \frac{{\widehat{\mathit{\beta }}}_{\mathrm{sca}}\left(n,k,\mathit{\lambda },D\right)}{{\widehat{\mathit{\beta }}}_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D\right)}},\text{(14)}& {\displaystyle }\begin{array}{rl}\widehat{g}\left(n,k,\mathit{\lambda },D\right)& ={\displaystyle \frac{\mathrm{1}}{{\widehat{\mathit{\beta }}}_{\mathrm{sca}}\left(n,k,\mathit{\lambda },D\right)}}\sum _{w=\mathrm{1}}^{\mathrm{121}}\\ & \cdot \left[{\displaystyle \frac{\mathit{\pi }{D}^{\mathrm{2}}}{\mathrm{4}}}\cdot {\text{SA}}_{\mathrm{w}}\left(\text{LWR},\text{HWR}\right)\right.\\ & \cdot Q_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR}\right)\\ & \cdot \text{SSA}\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR}\right)\\ & \cdot g\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR}\right)\\ & \left.\cdot f_{\mathrm{w}}\left(\text{LWR},\text{HWR}\right)\right],\end{array}\text{(15)}& {\displaystyle }\begin{array}{rl}\widehat{P_{ij}}\left(n,k,\mathit{\lambda },D,\mathit{\theta }\right)& ={\displaystyle \frac{\mathrm{1}}{{\widehat{\mathit{\beta }}}_{\mathrm{sca}}\left(n,k,\mathit{\lambda },D\right)}}\sum _{w=\mathrm{1}}^{\mathrm{121}}\\ & \cdot \left[{\displaystyle \frac{\mathit{\pi }{D}^{\mathrm{2}}}{\mathrm{4}}}\cdot {\text{SA}}_{\mathrm{w}}\left(\text{LWR},\text{HWR}\right)\right.\\ & \cdot Q_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR}\right)\\ & \cdot \text{SSA}\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR}\right)\\ & \cdot P_{ij}\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR},\mathit{\theta }\right)\\ & \left.\cdot f_{\mathrm{w}}\left(\text{LWR},\text{HWR}\right)\right],\end{array}\text{(16)}& {\displaystyle }\widehat{\mathit{\delta }}\left(n,k,\mathit{\lambda },D\right)={\displaystyle \frac{\widehat{P_{\mathrm{11}}}\left(n,k,\mathit{\lambda },D,\mathrm{180}{}^{\circ }\right)-\widehat{P_{\mathrm{22}}}\left(n,k,\mathit{\lambda },D,\mathrm{180}{}^{\circ }\right)}{\widehat{P_{\mathrm{11}}}\left(n,k,\mathit{\lambda },D,\mathrm{180}{}^{\circ }\right)+\widehat{P_{\mathrm{22}}}\left(n,k,\mathit{\lambda },D,\mathrm{180}{}^{\circ }\right)}},\text{(17)}& {\displaystyle }\widehat{S}\left(n,k,\mathit{\lambda },D\right)={\displaystyle \frac{\mathrm{4}\mathit{\pi }}{\widehat{\text{SSA}}\left(n,k,\mathit{\lambda },D\right)\cdot \widehat{P_{\mathrm{11}}}\left(n,k,\mathit{\lambda },D,\mathrm{180}{}^{\circ }\right)}},\text{(18)}& {\displaystyle }\begin{array}{rl}{\widehat{\mathit{\beta }}}_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D\right)& =\sum _{w=\mathrm{1}}^{\mathrm{121}}\left[{\displaystyle \frac{\mathit{\pi }{D}^{\mathrm{2}}}{\mathrm{4}}}\cdot {\text{SA}}_{\mathrm{w}}\left(\text{LWR},\text{HWR}\right)\right.\\ & \cdot Q_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR}\right)\\ & \left.\cdot f_{\mathrm{w}}\left(\text{LWR},\text{HWR}\right)\right],\end{array}\text{(19)}& {\displaystyle }\begin{array}{rl}{\widehat{\mathit{\beta }}}_{\mathrm{sca}}\left(n,k,\mathit{\lambda },D\right)& =\sum _{w=\mathrm{1}}^{\mathrm{121}}\left[{\displaystyle \frac{\mathit{\pi }{D}^{\mathrm{2}}}{\mathrm{4}}}\cdot {\text{SA}}_{\mathrm{w}}\left(\text{LWR},\text{HWR}\right)\right.\\ & \cdot Q_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR}\right)\\ & \cdot \text{SSA}\left(n,k,\mathit{\lambda },D,\text{LWR},\text{HWR}\right)\\ & \left.\cdot f_{\mathrm{w}}\left(\text{LWR},\text{HWR}\right)\right],\end{array}\end{array}$$

where ij=11, 12, 22, 33, 34, and 44 denote the six independent elements of the 4×4 scattering matrix, ${\widehat{\mathit{\beta }}}_{\mathrm{ext}}$ and ${\widehat{\mathit{\beta }}}_{\mathrm{sca}}$ are, respectively, the bulk volume extinction and scattering coefficients, and f_w(LWR,HWR) is the normalized weighting factor of the wth particle shape among the total 121 particle shapes, such that the sum of the 121 weighting factors yields unity. These weighting factors were calculated from the two lognormal distributions of LWR and HWR (Eqs. 9 and 10). Note that the upper limits of LWR and HWR are both 3.3 in the Meng et al. (2010) database, whereas observations find that dust particles can be more aspherical (Huang et al., 2020). For a dust particle with a LWR (or HWR) larger than 3.3, we assume its LWR (or HWR) is 3.3. Future database development to include these highly aspherical shapes is highly recommended. SA_w(LWR,HWR) is the ratio between the projected surface area of an ellipsoidal dust particle and the projected surface area of the volume-equivalent spherical dust particle, with the ellipsoidal dust particle having the wth particle shape among the total 121 particle shapes. We use this conversion factor to bridge the gap between two different definitions of extinction efficiency. The Meng et al. (2010) database calculated the extinction efficiency with regards to the projected surface area of the ellipsoidal particle, whereas global aerosol models use the extinction efficiency with regards to the projected surface area of the volume-equivalent sphere (Kok et al., 2017). Since an ellipsoidal particle has a larger surface area than its volume-equivalent spherical particle, SA_w(LWR,HWR) always exceeds unity. That is, although the 121 extinction efficiencies of the 121 shapes in Meng et al. (2010) approach an asymptotic value of 2 at large particle sizes (based on optical theorem of extinction; see Eq. (3.3.27) of Liou, 2002), the output extinction efficiency, ${\widehat{Q}}_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D\right)$, can be larger than 2 at large particle sizes (see Fig. 2), since they are corrected to account for SA_w(LWR,HWR).

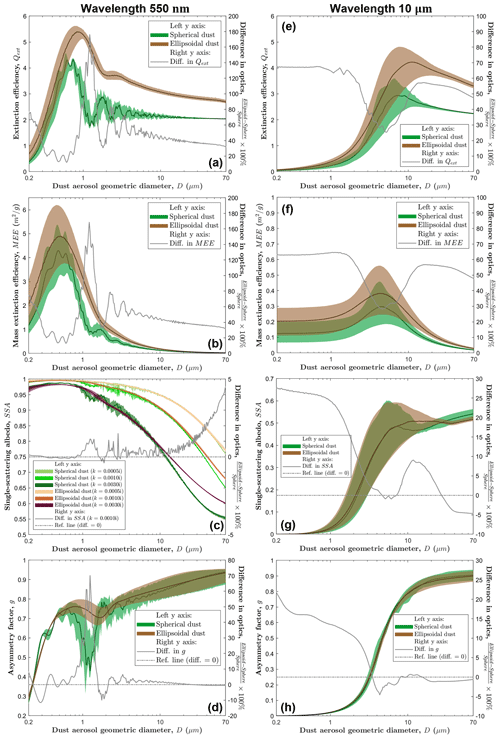
Figure 2 Single-scattering properties of spherical and triaxial ellipsoidal dust aerosols in the shortwave and longwave spectra. The left column includes (a) extinction efficiency Q_ext, (b) mass extinction efficiency MEE, (c) single-scattering albedo SSA, and (d) asymmetry factor g as a function of dust geometric diameter D at the wavelength of 550 nm. The right column includes (e) Q_ext, (f) MEE, (g) SSA, and (h) g as a function of D at the wavelength of 10 µm. In each plot, the left y axis corresponds to the single-scattering properties of spherical (in green) and ellipsoidal dust aerosols (in brown); the central lines denote the medians, and the shaded ranges represent the 95 % confidence intervals. The right y axis corresponds to the difference in the median single-scattering properties of the two shape approximations (in gray). The uncertainties in spherical dust optics are due to uncertainties in the dust refractive index (see Sect. 2.3), and the uncertainties in ellipsoidal dust optics are due to uncertainties in the dust refractive index and dust shape distributions (see Sect. 2.2 and 2.3). Panel (c) shows SSA at three different imaginary dust refractive indices (i.e., k=0.0005i, 0.001i, and 0.003i) with the confidence intervals arising from uncertainties in the real dust refractive index and dust shape distributions. The gray line in panel (c) denotes the difference in the median SSA of the two shape approximations at k=0.001i.

Using the equations above, we obtain the single-scattering properties of ellipsoidal dust ensembles constrained by measured dust shape distributions. The obtained ellipsoidal dust optics for use in global aerosol models ($\widehat{\text{MEE}}$, $\widehat{\text{SSA}}$, and $\widehat{g}$) are in a 4-dimensional (4-D) space, resolved by the real and imaginary parts of the dust refractive index, light wavelength, and dust volume-equivalent diameter. The obtained ellipsoidal dust optics for use by remote sensing retrievals are either in a 4-D space (for $\widehat{\mathit{\delta }}$ and $\widehat{S}$) or in a 5-D space (for $\widehat{P_{ij}}$), with an extra dimension as the scattering angle. We provided a publicly accessible repository with the lookup tables containing the ellipsoidal dust optics in these 4-D and 5-D spaces (see the code and data availability section at the end of the paper).

2.3 Observations to evaluate the simulated dust optics

We treat the observations of dust optics as the ground truth to evaluate our obtained ellipsoidal dust optics (Sect. 2.2) and the spherical and spheroidal dust optics used in previous studies. In this section, we first introduce laboratory observations of the scattering matrix and field observations of the linear depolarization ratio and lidar ratio. Second, we introduce the spherical and spheroidal dust optics used in most global aerosol models and remote sensing retrieval algorithms. Third, we integrate the size-resolved spherical, spheroidal, and ellipsoidal dust optics simulations over the dust particle size distributions observed for the laboratory and field observations. This integration enables comparisons on an equal footing, since the three optics simulations are size-resolved, whereas the observations were obtained for a mixture of dust aerosols with various particle sizes. Finally, we calculate the root mean square errors between the optics simulations and observations to quantify the performance of the three optics simulations.

The Amsterdam–Granada Light Scattering Database (AGLSD; Muñoz et al., 2012) is publicly accessible (see code and data availability section) and has been widely regarded as the standard to evaluate dust optical models (e.g., Nousiainen and Vermeulen, 2003; Dubovik et al., 2006; Merikallio et al., 2011; Lindqvist et al., 2014; Saito and Yang, 2021). The AGLSD contains laboratory measurements of the scattering matrices at two visible wavelengths of tens of samples with simultaneous measurements of the particle size distributions of these samples. Among these samples, we select two dust samples (i.e., newGobi and newSaharaOSN) and one mineral sample (i.e., feldspar) to evaluate the simulated dust optics for the following reasons. The two dust samples were collected, respectively, during an intense Gobi dust event reaching Beijing (China) in 2006 and an intense Saharan dust event reaching the Observatory of Sierra Nevada in Granada (Spain) in 2004 (Gómez Martín et al., 2021). These two samples are deposited dust aerosols, which are different from the other mineral samples included in AGLSD that were either purchased from commercial sources or generated in the lab by grinding mineral rocks and are thus less accurate representations of dust aerosols (Muñoz et al., 2012; Gómez Martín et al., 2021). In addition to the two dust samples, we also select the mineral sample feldspar. Although the sample feldspar was generated from ground feldspar rocks (Volten et al., 2001), and its representativeness for natural dust aerosols remains uncertain, we still select it because it is the only sample used to constrain the retrieval algorithm of AERONET (AErosol RObotic NETwork; Dubovik et al., 2006), as the newGobi and newSaharaOSN samples have only recently become available (Gómez Martín et al., 2021).

A range of field campaigns has measured the linear depolarization ratio and lidar ratio for Saharan and Asian dust aerosols. During these field campaigns, ground-based or aircraft-carried lidars measured the linear depolarization ratio and lidar ratio of dust plumes at the three common lidar wavelengths of 355, 532, and 1064 nm. We combine the measurement compilations of Tesche et al. (2019) and Saito and Yang (2021) and a new measurement study published after 2021 (i.e., Haarig et al., 2022). This yields a total of six datasets of the linear depolarization ratio and eight datasets of lidar ratio at three wavelengths (Tesche et al., 2009, 2011; Groß et al., 2011, 2015; Burton et al., 2015; Haarig et al., 2017, 2022; Hofer et al., 2020; Hu et al., 2020). We neglect the minor effects of dust multiple scattering and dust mixing with other aerosols on the observation results, as Tesche et al. (2019) and Saito and Yang (2021) did.

Regarding the optics simulations, most global aerosol models use spherical dust optics (Fig. 1a), and most remote sensing retrieval algorithms use spheroidal dust optics (Fig. 1b and c) with a shape distribution that conflicts with observations. Aerosol models and retrieval algorithms use lookup tables containing precalculated dust optics to reduce the computational costs. The lookup table of most aerosol models was calculated by the Lorenz–Mie theory (Liou, 2002). The most widely used lookup table of retrieval algorithms was calculated by Dubovik et al. (2006), using the following three steps. First, Dubovik et al. (2006) combined two computational methods (T matrix method and geometric-optics–integral-equation method) to calculate the spheroidal dust optics resolved in a 5-D space (i.e., n, k, λ, D, and length-to-height ratio). Second, they used these 5-D optics to retrieve the probability distribution of length-to-height ratio that enables the best agreement with the observed scattering matrix of AGLSD sample feldspar (see Fig. 13 of Dubovik et al., 2006). Finally, Dubovik et al. (2006) integrated the 5-D optics over the retrieved distribution of length-to-height ratio to obtain the spheroidal dust optics in a 4-D space (i.e., n, k, λ, and D). Dubovik et al. (2006)'s lookup table containing these spheroidal dust optics in the 4-D space has been used in many retrieval algorithms (for example, AERONET and Deep Blue of MODIS; Hsu et al., 2019). That is, these remote sensing retrievals chose their dust shape distribution as being the one that resulted in the best fit between the simulated scattering matrix and the observed scattering matrix of the AGLSD sample feldspar; however, this shape distribution conflicts with measurements of dust shape and is substantially less aspherical than natural dust aerosols (Fig. 1e; Kandler et al., 2007, 2009, 2011; Huang et al., 2020).

We use the observations of dust optics as the ground truth to evaluate the spherical, spheroidal, and ellipsoidal dust optics simulations. However, the three optics simulations are resolved by dust particle size and refractive index, whereas the observations were obtained for a mixture of dust aerosols with various sizes and mineral compositions. The AGLSD laboratory observations measured the particle size distributions (PSDs) of the samples but did not measure their refractive indices, whereas the field lidar observations did not measure the PSDs or the refractive index of dust plumes. To enable comparisons between the optics simulations and observations on an equal footing, we make the following three assumptions about PSDs and the refractive index. First, for the three AGLSD samples (i.e., newGobi, newSaharaOSN, and feldspar), we assume that the PSDs measured by AGLSD are accurate; for the dust plumes observed by field lidar observations across the world, we use the dust PSDs obtained by Adebiyi and Kok (2020), who presented a globally representative PSD of atmospheric dust by leveraging aircraft observations and model simulations. Second, we set the cutoff diameter of all three optics simulations at 63 µm because the PSDs of the two AGLSD samples (i.e., newGobi and newSaharaOSN) are coarser than the cutoff diameter of the lookup table (i.e., 63 µm) in Dubovik et al. (2006). Third, for the three AGLSD samples and dust plumes observed by field lidar observations, we take the dust refractive index as $\mathrm{1.53}\pm \mathrm{0.03}-i\times {\mathrm{10}}^{-\mathrm{2.75}\pm \mathrm{0.25}}$, covering the globally representative ranges in previous studies (i.e., summarized in Kok et al., 2017; Di Biagio et al., 2017, 2019). With the three assumptions above, we integrated the size-resolved scattering matrix of spherical, spheroidal, and ellipsoidal dust optics simulations, $\widehat{P_{ij}}\left(n,k,\mathit{\lambda },D,\mathit{\theta }\right)$, over the number PSDs of the three AGLSD samples and Adebiyi and Kok (2020), $\frac{\mathrm{d}N}{\mathrm{d}\ln D}$, as follows (Liou, 2002; Grainger, 2022):

$$\begin{array}{}\text{(20)}& \begin{array}{rl}\widehat{P_{ij}}\left(n,k,\mathit{\lambda },\mathit{\theta }\right)& ={\displaystyle \frac{\mathrm{1}}{{\int }_{D_{\min }}^{D_{\max }}\frac{\mathrm{d}N}{\mathrm{d}\ln D}\mathrm{d}\ln D}}\\ & \cdot \underset{D_{\min }}{\overset{D_{\max }}{\int }}\left[{\displaystyle \frac{\mathit{\pi }{D}^{\mathrm{2}}}{\mathrm{4}}}\cdot {\widehat{Q}}_{\mathrm{ext}}\left(n,k,\mathit{\lambda },D\right)\right.\\ & \cdot \widehat{\text{SSA}}\left(n,k,\mathit{\lambda },D\right)\cdot \widehat{P_{ij}}\left(n,k,\mathit{\lambda },D,\mathit{\theta }\right)\\ & \left.\cdot {\displaystyle \frac{\mathrm{d}N}{\mathrm{d}\ln D}}\right]\mathrm{d}\ln D.\end{array}\end{array}$$

We then used the scattering matrix of bulk dust aerosols obtained from Eq. (20) to calculate the simulated linear depolarization ratio and lidar ratio of bulk dust aerosols as follows:

$$\begin{array}{}\text{(21)}& {\displaystyle }\widehat{\mathit{\delta }}\left(n,k,\mathit{\lambda }\right)={\displaystyle \frac{\widehat{P_{\mathrm{11}}}\left(n,k,\mathit{\lambda },\mathrm{180}{}^{\circ }\right)-\widehat{P_{\mathrm{22}}}\left(n,k,\mathit{\lambda },\mathrm{180}{}^{\circ }\right)}{\widehat{P_{\mathrm{11}}}\left(n,k,\mathit{\lambda },\mathrm{180}{}^{\circ }\right)+\widehat{P_{\mathrm{22}}}\left(n,k,\mathit{\lambda },\mathrm{180}{}^{\circ }\right)}},\text{(22)}& {\displaystyle }\widehat{S}\left(n,k,\mathit{\lambda }\right)={\displaystyle \frac{\mathrm{4}\mathit{\pi }}{\widehat{\text{SSA}}\left(n,k,\mathit{\lambda }\right)\cdot \widehat{P_{\mathrm{11}}}\left(n,k,\mathit{\lambda },\mathrm{180}{}^{\circ }\right)}}.\end{array}$$

As such, we obtained the simulated optics of bulk spherical, spheroidal, and ellipsoidal dust aerosols for the range of the globally representative dust refractive index at the two AGLSD wavelengths and the three lidar wavelengths. These optics simulations can be compared with the optics observations to evaluate the performance of the three optics simulations. We used the root mean square error (RMSE) to quantify the agreement between the observed and simulated scattering matrix at forward-, side-, and backscattering angles. Specifically, we first interpolate the simulated scattering matrix onto the same scattering angles used by the AGLSD observations. We then calculated the RMSE as follows (Merikallio et al., 2011; Lindqvist et al., 2014):

$$\begin{array}{}\text{(23)}& {\displaystyle }\begin{array}{rl}& \text{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}{\sum }_{{\mathit{\theta }}_{\mathrm{1}}}^{{\mathit{\theta }}_{\mathrm{2}}}{\left[{\log }_{\mathrm{10}}\left({\displaystyle \frac{P_{ij,\mathrm{obs}}\left(\mathit{\theta }\right)}{P_{\mathrm{11},\mathrm{obs}}\left(\mathrm{30}{}^{\circ }\right)}}\right)-{\log }_{\mathrm{10}}\left({\displaystyle \frac{P_{ij,\mathrm{sim}}\left(\mathit{\theta }\right)}{P_{\mathrm{11},\mathrm{sim}}\left(\mathrm{30}{}^{\circ }\right)}}\right)\right]}^{\mathrm{2}}},\\ & ij=\mathrm{11}\end{array}\text{(24)}& {\displaystyle }\mathrm{\text{RMSE}}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}{\sum }_{{\mathit{\theta }}_{\mathrm{1}}}^{{\mathit{\theta }}_{\mathrm{2}}}{\left[{\displaystyle \frac{P_{ij,\mathrm{obs}}\left(\mathit{\theta }\right)}{P_{\mathrm{11},\mathrm{obs}}\left(\mathit{\theta }\right)}}-{\displaystyle \frac{P_{ij,\mathrm{sim}}\left(\mathit{\theta }\right)}{P_{\mathrm{11},\mathrm{sim}}\left(\mathit{\theta }\right)}}\right]}^{\mathrm{2}}},ij=\mathrm{12}\text{ and }\mathrm{22},\end{array}$$

where the RMSE of P₁₁ is calculated in logarithmic space because P₁₁ varies over several orders of magnitude, and N is the number of data points within the scattering angle range [θ₁, θ₂]. The scattering angle ranges are, respectively, $\left[\mathrm{5}{}^{\circ },\mathrm{35}{}^{\circ }\right]$ at the forward-scattering direction, $\left[\mathrm{75}{}^{\circ },\mathrm{105}{}^{\circ }\right]$ at the side-scattering direction, and $\left[\mathrm{143}{}^{\circ },\mathrm{173}{}^{\circ }\right]$ at the backscattering direction. The AGLSD observed scattering matrix at θ<5^∘ and θ>173^∘ is not available due to technical difficulties in measuring at these angles (Volten et al., 2001; Muñoz et al., 2012; Gómez Martín et al., 2021). We used Eqs. (23) and (24) to compare the RMSEs between the three optics simulations (i.e., spherical, spheroidal, and ellipsoidal dust optics) and the AGLSD observations of three samples (i.e., newGobi, newSaharaOSN, and feldspar) at two visible wavelengths.

3 Results

We obtained dust single-scattering properties by approximating dust as triaxial ellipsoidal particles with observationally constrained shape distributions. We compared these ellipsoidal dust optics with the spherical dust optics used in most global aerosol models and spheroidal dust optics used in most remote sensing retrievals. These comparisons help quantify the biases in global aerosol models and remote sensing retrievals due to problematic dust shape approximations.

We find that, relative to ellipsoidal dust optics, the spherical dust optics used in most global aerosol models underestimate the four key dust single-scattering properties for almost all dust sizes in both the shortwave and longwave spectra. First, most aerosol models underestimate the extinction efficiency (Q_ext) and mass extinction efficiency (MEE) by 20 % to 180 % in the shortwave spectrum (Fig. 2a and b) and by 30 % to 70 % in the longwave spectrum (Fig. 2e and f). The peak magnitude difference between the two sets of optical properties occurs at dust sizes slightly larger than the wavelength in the shortwave spectrum; at $D=\sim \mathrm{1}$ µm, aerosol models underestimate Q_ext by ∼3 and underestimate MEE by ∼1 m² g⁻¹. In the longwave spectrum, the peak magnitude difference occurs at dust sizes comparable to the wavelength; at $D=\sim \mathrm{10}$ µm, aerosol models underestimate Q_ext by ∼1.5 and underestimate MEE by ∼ 0.1 m² g⁻¹. Second, most aerosol models underestimate the single-scattering albedo (SSA) by up to 5 % in the shortwave spectrum (Fig. 2c) and by up to 25 % in the longwave spectrum (Fig. 2g). The magnitude difference between the two sets of optics in general increases with dust size and imaginary dust refractive index in both the shortwave and longwave spectra. Finally, most aerosol models slightly underestimate the asymmetry factor (g) at most dust sizes (Fig. 2d and h), except at $D=\sim \mathrm{1}$ µm in the shortwave spectrum, where aerosol models underestimate g by up to 70 % (Fig. 2d).

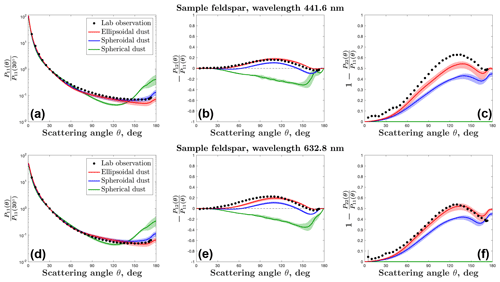
Figure 3 Comparison of the laboratory-measured scattering matrix of AGLSD mineral sample feldspar against the spherical, spheroidal, and ellipsoidal dust optics simulations at the wavelengths of 441.6 nm (a–c) and 632.8 nm (d–f). For the three simulations, the central lines denote the medians, and the shaded ranges represent the 95 % confidence intervals; these uncertainties are due to uncertainties in the dust refractive index and dust shape distributions (see Sect. 2.2 and 2.3).

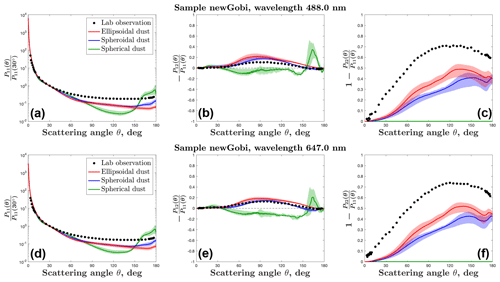
Figure 4 Same as Fig. 3, except for a comparison of the laboratory-measured scattering matrix of AGLSD dust sample newGobi against the spherical, spheroidal, and ellipsoidal dust optics simulations at the wavelengths of 488.0 and 647.0 nm.

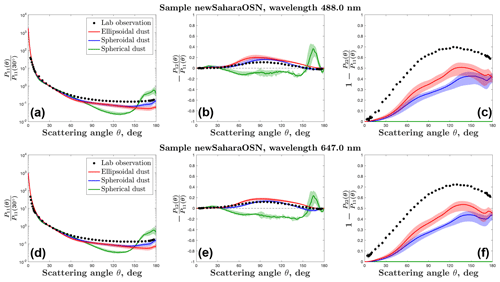
Figure 5 Same as Fig. 3, except for comparison of the laboratory-measured scattering matrix of AGLSD dust sample newSaharaOSN against the spherical, spheroidal, and ellipsoidal dust optics simulations at the wavelengths of 488.0 and 647.0 nm.

We further find that the ellipsoidal dust optics can reproduce the laboratory-measured phase function (i.e., P₁₁) and degree of linear polarization (i.e., $-\frac{P_{\mathrm{12}}}{P_{\mathrm{11}}}$) of AGLSD sample feldspar substantially better than the spherical and spheroidal dust optics (Fig. 3); however, it does not perform better than the spheroidal dust optics in reproducing the other two AGLSD samples (i.e., newGobi and newSaharaOSN; Figs. 4 and 5). Using the RMSE to quantify the disagreement between observation and simulation, the RMSEs between the laboratory measurements of feldspar optics and the ellipsoidal dust optics are the least at all scattering angles (Fig. 6). However, when comparing against the observations of newGobi and newSaharaOSN, the ellipsoidal dust optics almost always have larger RMSEs than the spheroidal dust optics (Fig. 6). Relative to all three AGLSD samples, the ellipsoidal dust optics underestimate the phase function at backscattering angles (Figs. 3, 4, and 5), resulting in an overestimation in the estimated lidar ratio (S; Fig. 7b; see Eq. 22 for the relationship between P₁₁ and S). Compiled field observations of Saharan and Asian dust aerosols find that S is ∼50 sr at the wavelengths of 355 and 532 nm and increases to ∼60 sr at 1064 nm (Fig. 7b). The ellipsoidal dust optics overestimate S by a factor of 2 and 1.3, respectively, at the two smaller and the largest wavelengths. The spheroidal dust optics can nicely reproduce S at 355 and 532 nm but somewhat underestimate S at 1064 nm (Fig. 7b). The spherical dust optics underestimate S by more than a factor of ∼3 at all wavelengths (Fig. 7b). For all three sets of optics, the magnitude difference between the observed and simulated S is consistent with the magnitude difference between the observed and simulated P₁₁ at the scattering angle of 180^∘ (Figs. 3, 4, and 5).

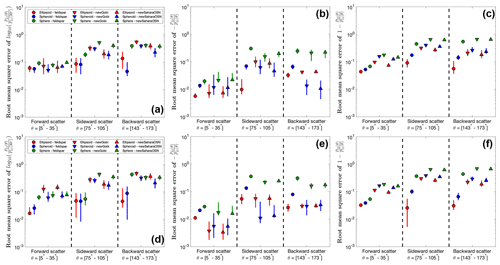
Figure 6 Root mean square errors (RMSEs) between the laboratory-measured and simulated scattering matrices at forward-, side-, and backscattering angles. The top column shows RMSEs at the smaller visible wavelength, which is 441.6 nm for AGLSD mineral sample feldspar and 488.0 nm for the other two dust samples (i.e., newGobi and newSaharaOSN). The bottom column shows RMSEs at the larger visible wavelength, which is 632.8 nm for feldspar and 647.0 nm for newGobi and newSaharaOSN. The vertical error bars denote uncertainties from the dust refractive index and dust shape distributions (see Sect. 2.2 and 2.3).

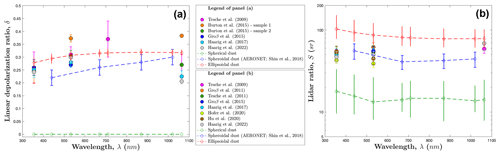
Figure 7 Comparison of the field-measured (a) linear depolarization ratio and (b) lidar ratio against the spherical, spheroidal, and ellipsoidal dust optics simulations as a function of light wavelength. In both plots, the closed markers denote field lidar measurements on Saharan dust aerosols (Tesche et al., 2009, 2011; Groß et al., 2011, 2015; Burton et al., 2015; Haarig et al., 2017, 2022) and Asian dust aerosols (Hofer et al., 2020; Hu et al., 2020). For the three simulations denoted in open markers, the vertical error bars denote uncertainties from the dust refractive index and dust shape distributions (see Sect. 2.2 and 2.3). The spheroidal dust optics are taken after Shin et al. (2018), who selected dust-dominated AERONET observations across the globe. The results of spherical and ellipsoidal dust optics simulations are presented at both the four AERONET wavelengths and the common lidar wavelengths.

In addition, we find that the ellipsoidal dust optics can reproduce the laboratory-measured depolarization of incident polarized light (i.e., $\mathrm{1}-\frac{P_{\mathrm{22}}}{P_{\mathrm{11}}}$) substantially better than the spherical and spheroidal dust optics. The RMSEs between the laboratory observations of the three AGLSD samples and the ellipsoidal dust optics are the least at all scattering angles (Fig. 6c and f). The ellipsoidal dust optics have lower RMSEs than the spheroidal and spherical dust optics, respectively, by a factor of 1.5 and 2 at forward-scattering angles, by a factor of 2 and 3 at side-scattering angles, and by a factor of 2 and 4 at backscattering angles (Fig. 6c and f). As a result of its excellent performance at backscattering angles, the ellipsoidal dust optics can reproduce the field lidar observations of the linear depolarization ratio (δ) substantially better than the spherical and spheroidal dust optics (Fig. 7a; see Eq. 21 for the relationship between $\frac{P_{\mathrm{22}}}{P_{\mathrm{11}}}$ and δ). Compiled field observations of Saharan and Asian dust aerosols find that δ is ∼0.25 at the wavelength of 355 nm, increases to ∼0.3 at 532 nm, increases to ∼0.36 at 710 nm, and then either stays constant or decreases to ∼0.26 at 1064 nm (Fig. 7a). The ellipsoidal dust optics reproduce both the magnitude and the wavelength dependency of the field observed δ. In contrast, the spheroidal dust optics predict an incorrect magnitude and wavelength dependency of δ, and the spherical dust optics incorrectly predict that δ is always zero because spherical dust particles do not depolarize incident light (see panels c and f of Figs. 3, 4, and 5).

4 Discussion

We obtained new dust single-scattering properties by approximating dust as triaxial ellipsoidal particles with observationally constrained shape distributions (Fig. 1). We find that, relative to these ellipsoidal dust optics, the spherical dust optics used in most aerosol models underestimate dust extinction efficiency, mass extinction efficiency, single-scattering albedo, and asymmetry parameter for almost all dust sizes in both the shortwave and longwave spectra (Fig. 2). Furthermore, we find that the ellipsoidal dust optics can reproduce the laboratory-measured depolarization of incident polarized light (Figs. 3, 4, and 5, and 6) and the field-measured linear depolarization ratio (Fig. 7a) substantially better than the spheroidal dust optics used in most retrieval algorithms. However, relative to laboratory observations, the ellipsoidal dust optics underestimate the phase function at backscattering angles by a factor of 2 (Figs. 3, 4, 5, and 6). As a result, the ellipsoidal dust optics overestimate the lidar ratio by a factor of ∼1.3 to 2 relative to field observations (Fig. 7b). These results provide insights into the following fundamental questions.

1. What is the implication of the missing dust asphericity in most global aerosol models?

2. What is the implication of the underestimated dust asphericity in most remote sensing retrieval algorithms?

3. How far are we from a perfect dust optical model?

4.1 Bias in global aerosol models due to missing dust asphericity

The approximation that dust aerosols are spherical, which is used in most global aerosol models (Fig. 1; Gliß et al., 2021), generates biases in dust single-scattering properties. Most aerosol models underestimate the four single-scattering properties (i.e., dust extinction efficiency Q_ext, mass extinction efficiency MEE, single-scattering albedo SSA, and asymmetry parameter g) because of the following two reasons. First, models underestimate the extinction efficiency because Q_ext scales with particle surface area, whereas models miss the surface area enhancement due to dust asphericity. Since a spherical dust particle has less surface area relative to a volume-equivalent ellipsoidal dust particle, the approximation of dust as spheres used in most models underestimates Q_ext. Note that our calculations neglect the dust surface roughness and sharp corners (see Sect. 4.3), which further increase the particle surface area, and therefore that most models possibly underestimate Q_ext and MEE more than our results indicate. Second, models underestimate the asymmetry parameter because an ellipsoidal dust particle scatters a larger portion of incident light in the forward direction than a volume-equivalent spherical dust particle (Nousianien and Kandler, 2015; Huang et al., 2021; Formenti et al., 2021). Since g scales with the portion of forward scattering, the spherical dust approximation used in most models underestimates g.

The biases in dust single-scattering properties used in most models have several key implications. First, models underestimate the mass extinction efficiency at the wavelength of 550 nm. Since many models are tuned to match the dust aerosol optical depth at 550 nm inferred from remote sensing observations (Ridley et al., 2016; Gliß et al., 2021), our finding that dust extinguishes more light per unit mass loading than models assume (Fig. 2b) indicates that models overestimate the global dust mass loading. This implication is supported by a previous study (i.e., Kok et al., 2017) that found that dust asphericity can enhance dust mass extinction efficiency by ∼30 %. Specifically, Kok et al. (2017) approximated dust as ellipsoidal particles with a lognormally distributed length-to-width ratio and a fixed height-to-width ratio (i.e., HWR=0.333). Relative to Kok et al. (2017), our results, which account for the lognormally distributed height-to-width ratio, find an even larger enhanced dust mass extinction efficiency by ∼10 %. This indicates that models overestimate the global dust mass loading by ∼40 %.

The second implication is that the dust single-scattering properties using the observed dust shape distributions can improve estimates of dust radiative effects. For example, Ito et al. (2021) used our single-scattering properties of ellipsoidal dust aerosols to reevaluate the dust radiative effects at the top of the atmosphere (TOA) and the surface. They integrated the rapid radiative transfer model for general circulation models (RRTMG) online within the Integrated Massively Parallel Atmospheric Chemical Transport (IMPACT) model (Ito et al., 2020). They found that accounting for dust asphericity barely changes the dust radiative effect at TOA, whereas dust asphericity strongly enhances the dust cooling effect at the surface (see Table 5 of Ito et al., 2021). Specifically, at TOA, dust asphericity enhances the cooling effect in the shortwave spectrum by 0.04 W m⁻² and enhances the warming effect in the longwave spectrum by 0.04 W m⁻², which cancels each other out. At the surface, dust asphericity enhances the cooling effect in the shortwave spectrum by 0.33 W m⁻² and enhances the warming effect in the longwave spectrum by 0.15 W m⁻², resulting in a net cooling with a magnitude of 0.18 W m⁻². That is, dust asphericity causes an atmospheric heating with a magnitude of 0.18 W m⁻². Since aspherical dust has a longer lifetime than spherical dust (Huang et al., 2020, 2021), this atmospheric heating can last longer than previously thought and possibly modify regional atmospheric dynamics, especially near dust source regions.

4.2 Bias in remote sensing retrievals due to underestimated dust asphericity

Most remote sensing retrieval algorithms approximate dust aerosols as being spheroidal particles with a shape distribution chosen to maximize agreement against the observed scattering matrix of AGLSD sample feldspar (Dubovik et al., 2006; Hsu et al., 2019). However, this shape distribution conflicts with observations of dust shape and substantially underestimates dust asphericity (Fig. 1). As a result, the shape approximation used in remote sensing retrievals might generate biases in the dust scattering matrix. Specifically, relative to AGLSD sample feldspar, the spheroidal dust optics, for which the shape distribution was fitted to maximize agreement with this sample, performs similarly to our ellipsoidal dust optics constrained by observed shape distributions (Figs. 3 and 6). Relative to the other two AGLSD samples (i.e., newGobi and newSaharaOSN), neither the spheroidal nor the ellipsoidal dust optics could reproduce the scattering matrix well, although the spheroidal dust optics perform better in reproducing the phase function, and the ellipsoidal dust optics perform better in reproducing the degree of linear polarization and the depolarization ratio (Figs. 4, 5, and 6). Drawing conclusions based on these two AGLSD samples is difficult because the spheroidal dust optics are constrained by sample feldspar instead of these two samples, making it difficult to link the biases in optics to the problematic dust shape approximation. These findings indicate that none of the three optics simulations (i.e., spherical, spheroidal, and ellipsoidal dust optics) could perfectly simulate the scattering matrix. On the one hand, the ellipsoidal dust optics could simulate the dust scattering matrix better than the spheroidal dust optics that are not constrained by the AGLSD sample feldspar. On the other hand, the ellipsoidal dust optics cannot simulate the phase function at backscattering angles well.

The biases in the dust scattering matrix can propagate into the depolarization ratio and lidar ratio, which are important to aerosol classification and aerosol retrieval algorithms of remote sensing products. For example, Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP), as the first spaceborne polarization lidar, has measured the vertical profiles of depolarization ratio and attenuated backscatter ratio across the globe since 2006 (Winker et al., 2007, 2009). CALIOP's aerosol classification algorithm first uses a threshold of attenuated backscatter ratio at the wavelength of 532 nm (i.e., $>\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$) to mask clouds (Winker et al., 2007; Omar et al., 2009). The classification algorithm then categorizes the remaining observations with a depolarization ratio larger than 0.2 at the wavelength of 532 nm as pure dust, in between 0.075 and 0.2 over the land (ocean) as polluted dust (dusty marine), and less than 0.075 as smoke (Kim et al., 2018). As such, CALIOP's aerosol classification algorithm offers vertical profiles of each aerosol subtype. By integrating the vertical profiles of aerosol subtypes against the lidar ratio of each aerosol type, CALIOP's retrieval algorithm calculates the aerosol optical depth (AOD) at the wavelength of 532 nm. CALIOP uses a fixed value of lidar ratio for each aerosol type, specifically 44±9 sr for pure dust and 55±22 sr for polluted dust in its latest version 4 retrieval algorithm (Kim et al., 2018). The retrieved AODs by CALIOP are significantly less than coincident AOD measurements and retrievals from various spaceborne, airborne, and ground-based products (Schuster et al., 2012; Omar et al., 2013; Kim et al., 2018). CALIOP might underestimate AOD in part because using a single value of lidar ratio and depolarization ratio remains problematic in representing the atmospheric aerosols whose microphysical properties vary spatiotemporally (Schuster et al., 2012; Kim et al., 2018).

The link between the lidar ratio and depolarization ratio and dust microphysical properties is also key to retrievals of dust microphysical properties. With the development of advanced lidar sensors, simultaneous observations of lidar ratio and depolarization ratio at multiple wavelengths are available (Freudenthaler et al., 2009; Tesche et al., 2009, 2011; Groß et al., 2015; Haarig et al., 2017, 2022). These datasets enable the inversion of dust microphysical properties (such as effective radius and the real and imaginary refractive index) once the lookup table on the relationship between the lidar ratio and depolarization ratio and dust microphysical properties is given (Müller et al., 2012, 2013). The lookup table of Dubovik et al. (2006) that contains spheroidal dust optics remains the most popular in the retrieval algorithms of lidar products (Müller et al., 2013; Tesche et al., 2019). The biases in the spheroidal dust optics due to underestimated dust asphericity can propagate into the aerosol classification and aerosol retrieval algorithms that further bias the estimated dust impacts.

Although the ellipsoidal dust optics show excellent agreement with the linear depolarization ratio (Fig. 7a), they overestimate the lidar ratio (Fig. 7b) by underestimating the backscattering intensity by a factor of ∼2 (Figs. 3, 4, and 5). The ellipsoidal dust optics have problematic backscattering intensities because of two possible reasons. First, the computational method used by the Meng et al. (2010) database to simulate ellipsoidal dust optics for particles with a size parameter $\ge \sim \mathrm{10}$ (see Table 2 of Meng et al., 2010), i.e., the improved geometric optics method (IGOM; Yang and Liou, 1996, 1997), underestimates the backscattering intensity by a factor of up to 2; IGOM underestimates the backscattering intensity because it ignores the coherent backscattering enhancement in the computations (Zhou and Yang, 2015; Zhou, 2018; Saito et al., 2021). This indicates an inherent error in the ellipsoidal optics that is not relevant to the dust shape constraints. Ongoing work on developing IGOM backscattering correction formulas can shed light on this issue (Saito and Yang, 2022). Second, we approximate dust as smooth particles and neglect the smaller-scale surface textures such as sharp corners and surface roughness that may affect the backscattering intensity. Saito et al. (2021) approximated dust as hexahedral particles with smooth surfaces and sharp corners and found that hexahedral dust has a good agreement with field measurements of the lidar ratio. Kemppinen et al. (2015) added surface roughness to smooth particles with sharp corners and found that surface roughening can reduce the backscattering intensity. Although the results of Kemppinen et al. (2015) indicate that adding surface roughness can widen the gap between modeled and measured backscattering intensity, the results of Kemppinen et al. (2015) were based on relatively fine dust particles with a size parameter less than 10 (i.e., diameter around 1.8 µm at 550 nm wavelength). A range of studies find that dust aerosols are much coarser and can be as large as 50 µm (Kok et al., 2017; Ryder et al., 2019; Adebiyi et al., 2020, 2023). No study has been conducted to investigate the results of roughening coarse and super-coarse dust particles. As a result, it remains unclear whether adding surface roughness for the ensemble of dust with various sizes will increase or decrease the gap between modeled and measured backscattering intensity. In addition, comparing the results of Saito et al. (2021) and Kemppinen et al. (2015) is difficult because these studies are based on different dust sizes, body shapes, surface corners and edges, and levels of surface roughening. Therefore, it remains unknown that which factor(s) (i.e., body shape, surface corners, and surface roughness) dominates the backscattering intensity and lidar ratio.

Table 1 A comparison between the ellipsoidal dust optical model (the present work) and the hexahedral dust optical model (Saito and Yang, 2021).

4.3 Recommendations for obtaining an improved dust optical model

We developed a new dust optical model accounting for observational constraints on dust shape distributions. The newly developed ellipsoidal dust optics are in better agreement with measurements of the scattering matrix and indicate that global aerosol models underestimate the four key single-scattering properties. Although the ellipsoidal dust optics show better agreement against measurements of the depolarization ratio than the spheroidal dust optics used in most remote sensing retrievals, they overestimate the lidar ratio by a factor of ∼2, making these optics problematic for remote sensing products that use the backscattering signal. We make the following recommendations for developing an improved dust optical model in the future, especially for remote sensing products that use the backscattering signal.

1. We encourage more laboratory observations of the scattering matrices of atmospheric dust aerosols with simultaneous measurements of the microphysical properties of these samples, namely their size distribution, refractive index, and shape distribution. The AGLSD sample feldspar had been the only dataset used in evaluating the simulated scattering matrix of dust optical models (Dubovik et al., 2006) until 2021, when two more samples (newGobi and newSaharaOSN) were published (Gómez Martín et al., 2021). These three samples are problematic for the following three reasons. First, their representativeness for atmospheric dust aerosols remains unknown, since the sample feldspar are not natural dust aerosols but rather were generated by grinding feldspar rocks and the two other samples are of deposited dust and are substantially coarser than is typical of atmospheric dust (Kok et al., 2017; Ryder et al., 2019; Adebiyi et al., 2020, 2023; Liu et al., 2019, 2020). Second, the refractive indices and shape distributions of the three samples were not measured simultaneously. Most studies evaluated their optical models assuming a wide range of refractive indices and particle shapes and used the averages as the evaluation results (e.g., Nousiainen and Vermeulen, 2003; Dubovik et al., 2006; Veihelmann et al., 2006; Merikallio et al., 2011; Lindqvist et al., 2014; Saito and Yang, 2021; Saito et al., 2021). Future simultaneous observations of refractive index and particle shape will help narrow the uncertainty range and identify the primary source of error. Finally, the exact backscattering and forward-scattering properties of the three samples are not available, since laboratory measurements struggle with technical difficulties at θ<5^∘ and θ>173^∘. Measurements at these exact scattering angles will serve as a benchmark for validating dust optical models (Miffre et al., 2016).

2. We encourage a systematic investigation of the relative impacts of dust body shape, surface corners, and surface roughness on the backscattering properties. We compared the advantages and shortcomings of the ellipsoidal dust model (the present work) and the recently published hexahedral dust model (Saito and Yang, 2021) in Table 1. Both optical models have strong application potential because they extensively cover wide ranges of size parameter and dust refractive index. On the one hand, the ellipsoidal dust model is more advanced than the hexahedral dust model in being constrained against measured dust shape distributions (see Sect. 2.2, Fig. 1, and Table 1). The hexahedral dust model is constrained against the degree of sphericity that is converted from the mean length-to-width ratio of Huang et al. (2020) and ignores the dust asphericity due to the height-to-width ratio (see Fig. 2a of Saito and Yang, 2021). As such, the hexahedral dust model underestimates the dust asphericity relative to dust shape observations. On the other hand, the hexahedral dust model is more advanced than the ellipsoidal dust model in accounting for sharp corners and coherent backscattering enhancement. The hexahedral dust model uses the physical geometric optics method (PGOM; Yang and Liou, 1996, 1997) to simulate the scattering properties for large dust particles (size parameter $\ge \sim \mathrm{50}$), which is more accurate than the improved geometric optics method (IGOM; Yang and Liou, 1996, 1997) used in the ellipsoidal dust model in reproducing the backscattering intensity and the lidar ratio (see the comparison between PGOM and IGOM in Fig. A1 of Saito et al., 2021). However, neither the ellipsoidal nor the hexahedral dust models can consistently reproduce the observed lidar ratio and depolarization ratio at all lidar wavelengths (Table 1). This occurs likely because neither of the two optical models accounts for the dust surface roughness, which can modify the scattering properties (Kemppinen et al., 2015; Saito et al., 2022). A future dust optical model that accounts for (1) dust body shape, (2) dust sharp corners, (3) dust surface roughness, and (4) coherent backscattering enhancement is highly encouraged.

3. Future work that defines descriptors for dust surface texture and observes the texture descriptors of atmospheric dust aerosols is needed. Although Huang et al. (2020) extensively compiled measurements of the macroscale shape characteristics of dust aerosols (i.e., dust body shape), few studies have measured the microscale shape characteristics of dust aerosols (i.e., surface corners and roughness). The two reasons that there are so few observations of the dust microscale shape are that these observations require more advanced microscopy techniques (Woodward et al., 2015) and that the descriptors to quantify the microscale shape characteristics are lacking (Nousiainen and Kandler, 2015). Advanced microscopy techniques have been used to image the microscale surface roughness of Arizona test dust less than 5 µm and ice crystals as large as ∼100 µm; however, good descriptors are still lacking (Magee et al., 2014). These issues make it difficult to evaluate whether a dust optical model that considers microscale shape characteristics does so in a realistic manner. Indeed, although a large number of studies have accounted for dust surface texture in developing dust optical models (e.g., Kalashnikova and Sokolik, 2004; Veihelmann et al., 2006; Gasteiger et al., 2011; Kemppinen et al., 2015; Kahnert et al., 2020), none of these shape approximations were validated against observations. The lack of good descriptors of dust surface texture thus remains a key challenge in comparing different dust optical models.

5 Conclusions

The single-scattering properties used in global aerosol models and remote sensing retrieval algorithms are critical for accurate simulations of dust distributions and dust impacts. Most global aerosol models approximate dust as spherical particles, whereas most remote sensing retrieval algorithms approximate dust as spheroidal particles with a shape distribution that conflicts with observations. These inconsistent and inaccurate shape assumptions generate biases in dust single-scattering properties.

Here, we obtain dust single-scattering properties by approximating dust as triaxial ellipsoidal particles with observationally constrained shape distributions. We find that, relative to the ellipsoidal dust optics obtained here, the spherical dust optics used in most global aerosol models underestimate dust extinction efficiency, mass extinction efficiency, single-scattering albedo, and asymmetry parameter for almost all dust sizes in both the shortwave and longwave spectra. These biases in the dust optics used in global aerosol models occur because these optics neglect or underestimate the effects of dust asphericity. The ellipsoidal dust optics developed in this work – and available at https://dustcomm.atmos.ucla.edu/ (last access: 20 February 2023) – can be used to improve the calculation of dust radiative effects in global aerosol models.

We further find that our ellipsoidal dust optics show a mixed performance in reproducing angle-dependent measurements that are important for remote sensing retrievals. These optics reproduce laboratory measurements of the depolarization of incident polarized light and field measurements of the linear depolarization ratio substantially better than the spheroidal dust optics that are used in most retrieval algorithms. However, the ellipsoidal dust optics underestimate laboratory observations of the phase function of dust at backscattering angles by a factor of ∼2. As a result, these optics overestimate the lidar ratio by a factor of ∼1.3 to 2 relative to field observations. Further improvements are thus needed to obtain a dust optical model that is sufficiently accurate at backscattering angles. In particular, future models should account for coherent backscattering enhancement, the macroscale shape characteristics (i.e., dust body shape), and the microscale shape characteristics (i.e., dust sharp corners and surface roughness).