A global climatology of ice-nucleating particles under cirrus conditions derived from model simulations with MADE3 in EMAC

Atmospheric aerosols can act as ice-nucleating particles (INPs), thereby influencing the formation and the microphysical properties of cirrus clouds, resulting in distinct climate effects. In addition to mineral dust and soot particles, laboratory experiments suggest crystalline ammonium sulfate and glassy organic particles as effective INPs in the cirrus regime. However, the impact of these new particle types at the global scale is still highly uncertain. Here, we present and analyse a global climatology of INPs derived from model simulations performed with a global aerosol–climate model coupled to a two-moment cloud microphysical scheme and a parametrization for aerosol-induced ice formation in cirrus clouds. This global INP climatology comprises mineral dust and soot particles as well as crystalline ammonium sulfate and glassy organics, including a simplified formulation of the particle phase state for the latter. By coupling the different INP types to the microphysical cirrus cloud scheme, their ice nucleation potential under cirrus conditions is analysed, considering possible competition mechanisms between different INPs. The simulated INP concentrations in the range of about 1 to 100 L⁻¹ agree well with in situ observations and other global model studies. We show that INP concentrations of glassy organics and crystalline ammonium sulfate are strongly related to the ambient conditions which often inhibit the glassy or crystalline phase respectively. Our model results suggest that glassy organic particles probably only have a minor influence, as INP concentrations are mostly low in the cirrus regime. On the other hand, crystalline ammonium sulfate often shows large INP concentrations, has the potential to influence ice nucleation in cirrus clouds, and should be taken into account in future model applications.

1 Introduction

Atmospheric aerosol particles can exert important influences on the global climate system by directly changing the Earth's energy budget via interactions with solar and terrestrial radiation (Boucher et al., 2013; Bellouin et al., 2020). Additionally, aerosol particles can act as cloud condensation nuclei and ice-nucleating particles (INPs), thereby influencing the formation of cloud droplets and ice crystals and, in turn, leading to additional climate effects (Boucher et al., 2013; Mülmenstädt and Feingold, 2018). However, these aerosol–cloud interactions are still poorly understood and are the subject of ongoing research activities (Mülmenstädt and Feingold, 2018; Bellouin et al., 2020; Murray et al., 2021). In particular, INP effects on cirrus clouds and their climatic impacts are highly uncertain (e.g. Kärcher, 2017; Kanji et al., 2017).

INPs can initiate the heterogeneous nucleation of ice crystals at lower supersaturations with respect to ice compared with the homogeneous freezing of liquid aerosols (Koop et al., 2000; Hoose and Möhler, 2012). This competition mechanism between heterogeneous and homogeneous nucleation for the available supersaturated water vapour crucially depends on the abundance of INPs and their freezing potential (Kärcher et al., 2006; Gasparini and Lohmann, 2016; McGraw et al., 2020). However, the atmospheric concentration of INPs and their global distribution are still poorly constrained, contributing a large part to the uncertainty in the quantification of the climatic impact of aerosol–cirrus interactions. A global analysis of INP concentrations is challenging, as in situ observations are scarce and have mostly targeted the mixed-phase temperature regime (Rogers et al., 2001a; DeMott et al., 2010; Schrod et al., 2017), while measurements under cirrus conditions are very limited. Additionally, measurements are typically limited in space and time (e.g. Rogers et al., 1998), complicating interpretations at the global scale. In the past, modelling studies applying global chemistry climate models have been performed to elucidate the global distribution of different INPs (e.g. Barahona et al., 2010; Hendricks et al., 2011; Penner et al., 2018). However, as the ice-nucleating potential of INPs is continually re-evaluated in laboratory measurements (Kanji et al., 2017) and new types of INP species have been suggested to have important influences (e.g. Ladino et al., 2014; Ignatius et al., 2016; Wilbourn et al., 2020), an updated picture of the global INP distribution is necessary.

Here, we present results from global model simulations of ice-nucleating aerosol particles and describe an up-to-date global climatology of INPs, including several major INP types in the cirrus regime, i.e. mineral dust, soot, crystalline ammonium sulfate, and glassy organics. We employ the atmospheric chemistry general circulation model EMAC (ECHAM/MESSy2 Atmospheric Chemistry model; Jöckel et al., 2010) including the MESSy (Modular Earth Submodel System) aerosol microphysics submodel MADE3 (Modal Aerosol Dynamics model for Europe, adapted for global applications, third generation; Kaiser et al., 2014). MADE3 is especially suited for the analysis of ice-nucleating aerosol processes, as it is able to simulate different particle compositions and mixing states, which influence important ice nucleation properties of the INPs. For instance, insoluble particles with and without relevant soluble coatings can be distinguished in different size ranges. The MADE3 aerosol is coupled to (cirrus) clouds via a two-moment cloud scheme (Kuebbeler et al., 2014), as described in detail by Righi et al. (2020). This allows one to analyse the ice nucleation potential of various INP types under cirrus conditions, including possible competition mechanisms between different INPs.

Mineral dust and soot particles, which are typically considered to be INPs in the cirrus regime (Möhler et al., 2006, 2008; Kulkarni et al., 2016), are represented in EMAC-MADE3 and coupled to the freezing scheme as described in Righi et al. (2020). This also includes the improved representation of mineral dust aerosol by employing an online calculation of wind-driven dust emissions (Tegen et al., 2002), as described in Beer et al. (2020). Furthermore, the model includes an additional tracer for tagging soot particles from specific sources, e.g. from aviation emissions (Righi et al., 2021), to analyse the global distribution of aviation soot INPs.

In addition to mineral dust and soot, other aerosol species have been reported to potentially nucleate ice in the cirrus regime. Several studies have described the ice nucleation potential of glassy organic particles (Murray et al., 2010; Ladino et al., 2014; Ignatius et al., 2016; Wagner et al., 2017), often well below the homogeneous freezing threshold. Atmospheric secondary organic aerosol (SOA) particles can exist in a highly viscous, amorphous state, depending on ambient temperature and humidity (Reid et al., 2018). This glassy state has been shown to be an essential requirement for a high freezing potential of organic particles (Ignatius et al., 2016). Typical biogenic SOA precursors are terpenes, a class of organic compounds emitted by various plants, especially in boreal forest regions, e.g. the monoterpene pinene (Laaksonen et al., 2008). Another common SOA precursor is isoprene, mainly emitted, for instance, from tropical rainforests (Guenther et al., 1995, 2006). Besides glassy organics, crystalline ammonium sulfate ((NH₄)₂SO₄) has been reported to be an effective INP under cirrus conditions (Abbatt et al., 2006; Wise et al., 2009; Baustian et al., 2010; Ladino et al., 2014). The phase state of ammonium sulfate particles is crucial for their ice nucleation potential, as only crystalline particles have been shown to initiate ice nucleation. Ammonium sulfate particles undergo phase transitions depending on the ambient temperature and humidity via a hysteresis process, i.e. the characteristic relative humidity of the transition from aqueous solution droplets to solid crystals, the efflorescence relative humidity (ERH), is different from that of the converse process. The deliquescence relative humidity (DRH) at which solid crystals dissociate and are transformed into solution droplets is typically larger than the ERH (Martin, 2000; Martin et al., 2003).

These new types of INPs, i.e. glassy organics and crystalline ammonium sulfate, have only rarely been considered in global modelling studies, and their potential for cirrus cloud and climate modifications is still highly uncertain (e.g. Abbatt et al., 2006; Penner et al., 2018; Zhu and Penner, 2020). Here, we include glassy organics and crystalline ammonium sulfate as INPs in the framework of EMAC-MADE3, including the representation of their phase state, i.e. glassy or crystalline respectively, depending on the simulated ambient temperature and relative humidity. These model improvements allow us to investigate the global distributions of a large suite of major INP types in the cirrus regime on a self-consistent climatological basis. The coupling of the applied aerosol submodel with a microphysical two-moment cloud scheme, including the major aerosol-induced cirrus formation pathways as well as their competition, allows one to further assess the importance of these INP types in cirrus cloud formation. Based on these modelling capabilities, new insights into aerosol–cirrus interaction mechanisms and their global variability are gained in this study.

The paper is organized as follows: in Sect. 2, we describe the modelling framework EMAC-MADE3 with a focus on the representation of crystalline ammonium sulfate and glassy organics and their corresponding phase characterization; the calculation of the number concentrations of potential INPs is described in detail in Sect. 3; the simulated aerosol concentrations of mineral dust, (aviation) soot, ammonium sulfate, and glassy organics are shown in Sect. 4; in Sect. 5, we analyse the global distribution of INP concentrations per species as well as the concentrations of nucleated ice crystals; and the main conclusions of this study are highlighted in Sect. 6.

The work presented in this paper is based, in part, on the PhD thesis by Christof Gerhard Beer (Beer, 2021), and some of the text appeared similarly therein.

2 Model description

2.1 EMAC-MADE3 model set-up

The EMAC model is a global numerical chemistry and climate simulation system, and it includes various submodels that describe tropospheric and middle-atmosphere processes. It uses the second version of MESSy to connect multi-institutional computer codes. The core atmospheric model is the ECHAM5 (fifth-generation European Centre Hamburg) general circulation model (Roeckner et al., 2006). In this work, we apply EMAC (ECHAM5 version 5.3.02, MESSy version 2.55) in the T63L31 configuration with spherical truncation of T63 (corresponding to a horizontal resolution of about $\mathrm{1.9}{}^{\circ }\times \mathrm{1.9}{}^{\circ }$) and 31 non-equidistant vertical layers from the surface to 10 hPa. The simulated time period covers the years 2009 to 2019, but the year 2009 is used as a spin-up and excluded from the evaluation. All simulations presented here are performed in nudged mode, i.e. model meteorology (temperature, winds, and logarithm of the surface pressure) is relaxed towards the ERA5 reanalysis data (Hersbach et al., 2020) for the same time period.

The MADE3 aerosol microphysics submodel simulates different aerosol species in nine log-normal modes that represent different particle sizes and mixing states. A detailed description of MADE3 as well as its application and evaluation as part of EMAC can be found in Kaiser et al. (2014, 2019).

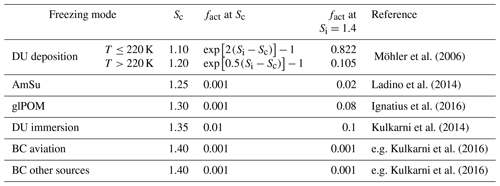
In this study, EMAC-MADE3 is employed in a coupled configuration that includes a two-moment cloud microphysical scheme based on Kuebbeler et al. (2014), employing a parametrization for aerosol-driven ice formation in cirrus clouds following Kärcher et al. (2006). The Kärcher et al. (2006) scheme considers the competition between various ice formation mechanisms for the available supersaturated water vapour, i.e. homogeneous freezing of solution droplets, deposition and immersion nucleation induced by INPs, and the growth of pre-existing ice crystals. In each of the heterogeneous freezing modes, the ice nucleation properties of the INPs are represented by two parameters, namely the active fraction (f_act) of ice-nucleating particles, which actually lead to the formation of ice crystals, and the critical supersaturation ratio with respect to ice (S_c), at which the freezing process is initiated. The model set-up has been extensively tuned and evaluated with respect to various cloud and radiation variables by Righi et al. (2020), with further model improvements described in Righi et al. (2021).

In this study, ice nucleation induced by mineral dust (DU), black carbon (BC, in the form of soot particles) from all sources except aviation, BC from aviation (BCair), glassy organic particles (glPOM), and crystalline ammonium sulfate (AmSu) is considered. The freezing properties of these INPs are summarized in Table 1. To our knowledge, there are only a few studies that have considered the specific phase state of ammonium sulfate and organic particles (i.e. crystalline or glassy respectively). Here, we assume the corresponding freezing properties of crystalline ammonium sulfate and glassy organics according to Ladino et al. (2014) and Ignatius et al. (2016) respectively. Dust immersion freezing has also rarely been investigated in laboratory experiments. In the original Kuebbeler et al. (2014) scheme, a value of S_c=1.3 for the onset of dust immersion freezing was assumed according to Möhler et al. (2008). Here, a slightly larger value of S_c=1.35 is used according to Kulkarni et al. (2014), where the mixed-phase regime at T=238 K and sulfuric acid coatings around dust particles are considered. Despite the mixed-phase temperature, this value is used as a more conservative assumption in the cirrus regime, as Möhler et al. (2008) only considered dust particles with organic coatings at very low temperatures (205 K < T < 210 K). For DU deposition freezing, following Kuebbeler et al. (2014), f_act is calculated depending on the supersaturation with respect to ice and the temperature. For BC, numerous different studies exist that investigate the freezing of soot particles from a variety of different sources. For example, Koehler et al. (2009) analysed various soot types, including soot resulting from burning aviation kerosene, and observed ice nucleation below the homogeneous freezing threshold. Kanji et al. (2011) measured onset S_c values between 1.3 and 1.5 for ice nucleation on graphite soot, while Chou et al. (2013) and Kulkarni et al. (2016) reported onset ice nucleation on fresh and aged diesel soot particles at S_c of around 1.4. Recently, the ice nucleation of BC at cirrus temperatures has been attributed to the pore condensation and freezing mechanism rather than deposition freezing (e.g. Marcolli, 2017; Mahrt et al., 2018; David et al., 2019; Mahrt et al., 2020). Cloud processing of soot particles (e.g. in contrails) has been shown to play a crucial role in this process, resulting in an enhancement of the freezing potential of soot by lowering the S_c (Mahrt et al., 2018, 2020). In this study, we assume a value of S_c=1.4 for ice nucleation induced by BC (including BC from aviation) in accordance with the wide range of results from measurements.

Möhler et al. (2006)Ladino et al. (2014)Ignatius et al. (2016)Kulkarni et al. (2014)Kulkarni et al. (2016)Kulkarni et al. (2016)

Table 1 Freezing properties of ice-nucleating particles in the cirrus regime assumed in this study, i.e. critical supersaturation (S_c) and activated fraction (f_act) at the freezing onset. S_i is the supersaturation with respect to ice. In addition to f_act values representative of the freezing onset, f_act values at about S_i=1.4 are used in the analysis.

The EMAC-MADE3 set-up applied here is largely based on the set-up described in Righi et al. (2021). We use the recent CMIP6 (Coupled Model Intercomparison Project Phase 6) emission inventory for anthropogenic and biomass burning emissions of aerosols and aerosol precursor species (van Marle et al., 2017; Hoesly et al., 2018) for the year 2014, in order to provide an emission set-up close to present-day conditions. Mineral dust emissions are calculated according to the online emission scheme of Tegen et al. (2002), as described and evaluated in Beer et al. (2020). We employ EMAC in the T63L31 resolution, in contrast to the T42L41 resolution in Righi et al. (2021), as this was shown to improve the simulated aerosol concentrations, especially for mineral dust, in the upper troposphere (Beer et al., 2020).

For this study, further developments of the model system were performed concerning the implementation of additional aerosol species that can act as ice-nucleating particles, i.e. glassy organics and crystalline ammonium sulfate. The model representation of these new particle types is described in the following (Sect. 3.1–3.3). The calculations of the number concentrations of potential INPs (i.e. glassy organics, crystalline ammonium sulfate, mineral dust, and black carbon) are presented in Sect. 3.4.

3 Implementation of additional ice-nucleating aerosol species

3.1 Black carbon from aviation

As described in Righi et al. (2021), an additional black carbon tracer for tagging soot emissions from the aviation sector (BCair) is used. BCair is implemented as an additional MADE3 aerosol tracer and is distributed in the same six modes as the standard BC tracers, namely insoluble and mixed Aitken, accumulation, and coarse mode. Compared to the standard BC tracer, BCair has the same physical properties and is subject to the same processes in the model.

3.2 Glassy organics

Similar to BCair and in addition to the standard POM (particulate organic matter) tracer, we include a MADE3 tracer for glassy organic particles (glPOM) that considers emissions of natural SOA precursors (e.g. terpenes), according to Guenther et al. (1995). The precursor gases include isoprene, monoterpenes, and other volatile organic compounds, which are mainly emitted from tropical woodlands, especially rainforests. In analogy to Kaiser et al. (2019), it is assumed that natural terpenes are transformed to SOA with a constant yield of 15 %, following Dentener et al. (2006). The resulting SOA species are assumed to irreversibly condense as particulate organic matter on pre-existing aerosol particles. To track SOA from natural terpenes, the condensed mass is assigned to the glPOM tracer.

Importantly, atmospheric SOA particles can be transformed into an amorphous, glassy state, with extremely high viscosities of η>10¹² Pa s (Koop et al., 2011), facilitating their ice-nucleating potential. This glass transition critically depends on the atmospheric conditions. If the ambient temperature decreases below a certain threshold temperature, namely the glass transition temperature (T_g), a liquid solution particle vitrifies and is transformed into a semi-solid, glassy state (Reid et al., 2018). For increasing temperatures, the reverse process, i.e. glass-to-liquid transition, occurs at the same specific temperature. T_g depends on the composition of the organic compound, and it increases with decreasing relative humidity (RH). For low humidity values (RH < 10 %), Koop et al. (2011) describe a T_g for an SOA estimate of around 270 K. Here, we use three different formulations for T_g depending on RH, assuming citric acid ($T_{\mathrm{g}}^{\left(\mathrm{1}\right)}$), glucose ($T_{\mathrm{g}}^{\left(\mathrm{2}\right)}$), and sucrose ($T_{\mathrm{g}}^{\left(\mathrm{3}\right)}$), which have been shown to be good proxies for atmospheric SOA (Baustian et al., 2013). T_g (in units of kelvin) is given in Baustian et al. (2013) for RH values between 0 % and 100 % for the three SOA proxies:

$$\begin{array}{}\text{(1a)}& {\displaystyle }& {\displaystyle }{T}_{\mathrm{g}}^{\left(\mathrm{1}\right)}\left(\mathrm{RH}\right)=\mathrm{277.14}-\mathrm{0.33}\mathrm{RH}-\mathrm{0.01}{\mathrm{RH}}^{\mathrm{2}},\text{(1b)}& {\displaystyle }& {\displaystyle }{T}_{\mathrm{g}}^{\left(\mathrm{2}\right)}\left(\mathrm{RH}\right)=\mathrm{293.26}+\mathrm{0.12}\mathrm{RH}-\mathrm{0.016}{\mathrm{RH}}^{\mathrm{2}},\text{(1c)}& {\displaystyle }& {\displaystyle }{T}_{\mathrm{g}}^{\left(\mathrm{3}\right)}\left(\mathrm{RH}\right)=\mathrm{333.94}-\mathrm{0.3}\mathrm{RH}-\mathrm{0.017}{\mathrm{RH}}^{\mathrm{2}}.\end{array}$$

The three different T_g(RH) curves are shown in Fig. S1 in the Supplement. The reference case for the model simulations is $T_{\mathrm{g}}^{\left(\mathrm{2}\right)}$(RH), and the other two estimates represent a lower and an upper boundary for T_g respectively. For the glPOM tracer, we only consider those cases which fulfil the glassy condition T<T_g.

3.3 Ammonium sulfate

Crystalline ammonium sulfate, in contrast to glPOM, requires the representation of a dedicated phase transition via a hysteresis process which depends on the relative humidity history. Efflorescence of aqueous ammonium sulfate particles occurs at a lower relative humidity (ERH) than the deliquescence of ammonium sulfate crystals (DRH). Due to the lack of a phase state characterization for MADE3 aerosol tracers, we represent crystalline ammonium sulfate as a passive aerosol tracer (AmSu) using the EMAC submodel PTRAC (Prognostic TRACers; Jöckel et al., 2008). For each PTRAC tracer, geometric mean particle radius, density, and geometric standard deviation are fixed at predefined constant values. As the number concentration of INPs is the central quantity for ice nucleation processes, AmSu is implemented as a number density tracer, and it is calculated from ammonium (NH₄) and sulfate (SO₄) input masses from MADE3 assuming characteristic particle sizes. To assess related uncertainties, we assume different representations of ammonium sulfate by defining three different PTRAC tracers:

• AmSu_mixS – crystalline ammonium sulfate particles with inclusions of other components and a 100 nm particle radius, representing typical MADE3 accumulation-mode sizes for polluted air. Only grid boxes where the fraction of NH₄ and SO₄ dominates the total aerosol dry mass (>50 %) are considered.

• AmSu_mixL – similar to AmSu_mixS but considering crystalline ammonium sulfate particles with inclusions of other components and a 250 nm particle radius, representing larger accumulation-mode particles. Again, only grid boxes dominated by NH₄ and SO₄ are considered.

• AmSu_ext – externally mixed crystalline ammonium sulfate (without inclusions) and a 100 nm particle radius, representing a control estimate for the crystalline ammonium sulfate particle number concentration, independent of the MADE3 representation of the mixing state. Here, all available ammonium and sulfate mass in the accumulation mode is considered, without the restriction to NH₄- and SO₄-dominated cases.

These AmSu tracers are calculated according to NH₄ and SO₄ input masses from MADE3 soluble and mixed accumulation modes. As AmSu_mixS and AmSu_mixL have different particle diameters, the total soluble and mixed accumulation-mode masses have to be separated into two fractions, depending on the intersection radius $R_{\mathrm{inter}}=(R_{{\mathrm{AmSu}}_{\mathrm{mixS}}}+R_{{\mathrm{AmSu}}_{\mathrm{mixL}}})/\mathrm{2}=\mathrm{175}$ nm, in analogy to the MADE3 mode renaming operation described in Kaiser et al. (2014). The accumulation modes are most relevant for ice nucleation induced by crystalline ammonium sulfate. Aitken-mode particles are too small to be efficient ice nuclei (e.g. Kanji et al., 2017), while coarse modes have only a few particles. However, as large coarse-mode particles can be highly efficient ice nuclei, we define two additional tracers for internally and externally mixed coarse ammonium sulfate (AmSu_mix,coa and AmSu_ext,coa), similar to the AmSu tracers described above, but with 1.75 and 1.0 µm particle radii respectively. These sizes are chosen analogous to the accumulation-mode tracers but are 1 order of magnitude larger, representing typical coarse-mode sizes¹. The specific density of AmSu tracers is set to 1770 kg m⁻³ (Rumble, 2004). The geometric standard deviations are defined in analogy to the MADE3 accumulation and coarse modes, i.e. σ_g=2.0 for the accumulation mode, and σ_g=2.2 for the coarse mode respectively (Kaiser et al., 2019). The calculations of AmSu tracers consider phase transitions depending on the relative humidity as well as changes in tracer concentrations due to removal processes in clouds and precipitation (dry deposition of AmSu is represented similarly to other aerosol tracers). The subroutines dealing with these calculations are part of the MADE3 submodel and are described in detail in the Supplement (Sect. S1).

3.4 Calculation of number concentrations of potential INPs

In order to realize ice nucleation induced by aerosol particles in the model, the corresponding aerosol tracers need to be coupled to the cloud parametrization in the EMAC CLOUD module. There, the number concentrations of potential INPs are calculated for the different ice formation modes in the mixed-phase and the cirrus regime, according to the procedure described in Righi et al. (2020). Potential INP numbers are multiplied by the respective ice-active fractions f_act to obtain the actual INP concentrations used as input for the cirrus cloud parametrization. Here, the calculations described in Righi et al. (2020) are expanded to include the additional INPs considered in this study, i.e. glPOM, AmSu, and BCair. The calculation of INP concentrations available for freezing events is calculated for every MADE3 mode, as described in detail in the Supplement (Sect. S2).

For the freezing of crystalline ammonium sulfate, the sum of the AmSu_mixS and AmSu_mixL number concentrations is considered, as these tracers provide a more detailed and realistic representation compared with AmSu_ext. As the cloud scheme considers additional increases in relative humidity due to subgrid-scale updraughts, AmSu freezing is only considered if S_c<DRH, as the particles would otherwise not be in the crystalline phase. For this condition the supersaturation with respect to ice is converted to the value with respect to liquid water using the formulations described by Murphy and Koop (2005), depending on the ratio of the vapour pressures of liquid water and ice respectively. As the cloud scheme requires information about the AmSu number concentrations per MADE3 mode, AmSu numbers are separated according to NH₄ and SO₄ masses in the MADE3 soluble and mixed modes. Additionally, possible inclusions in AmSu particles (e.g. DU) have to be subtracted from the corresponding concentration in other freezing modes.

Generally, in every mode where glPOM is present, the number of glPOM INPs is calculated first and subtracted from the number in the other freezing modes, as glassy organics are assumed to form a shell around other particles (e.g. Smith et al., 2012, 2013; Schill et al., 2014; Saukko et al., 2015). This shell is then the relevant part of the particle for the ice nucleation processes. An alternative formulation for glPOM freezing, considering glPOM INPs only for grid boxes where the glPOM mass fraction (with respect to the total mass in the mode) exceeds certain thresholds (e.g. 0.3 or 0.5), resulted in negligible number concentrations of potential glPOM INPs.

4 Atmospheric distribution of aerosols acting as ice-nucleating particles

In this section, we present the atmospheric distributions of the aerosol species that act as ice-nucleating particles in the model, i.e. mineral dust, black carbon, glassy organic particles, and crystalline ammonium sulfate. These simulated aerosol concentrations are the input for the ice nucleation scheme, where the actual number concentration of the potential INPs is calculated (see Sect. 3.4).

4.1 Mineral dust and black carbon

Figure 1 shows the dust, BC, and aviation BC mass concentrations as simulated by EMAC-MADE3 at 300 hPa (Fig. 1a, c, e) as well as the zonal-mean vertical distribution (Fig. 1b, d, f). As mineral dust is a primary aerosol, dust concentrations in the atmosphere are strongly connected to the dust emission regions (most prominently the Sahara and Arabian deserts). Concentrations of up to 0.5 µg m⁻³ are reached in the upper troposphere over parts of northern Africa, with a strong vertical gradient towards the largest concentrations close to the surface. A more detailed description and evaluation of mineral dust in the EMAC-MADE3 model is presented in Beer et al. (2020).

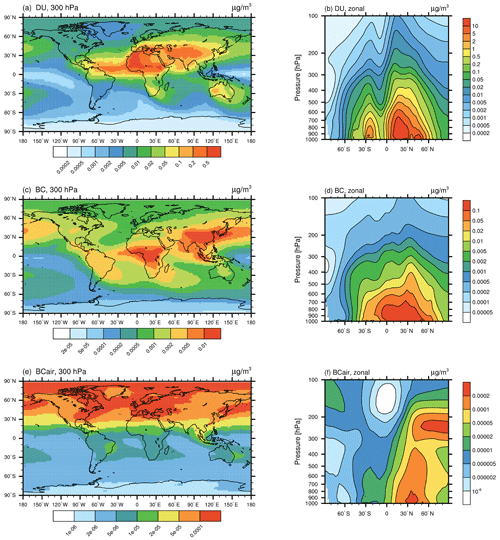
Figure 1 Global distribution of the mass concentrations of mineral dust (DU; a, b), black carbon (BC; c, d), and black carbon from aviation emissions (BCair; e, f) in micrograms per cubic metre (µg m⁻³), simulated with EMAC-MADE3 considering the multi-year average over the simulation period (2010–2019). Panels (a), (c), and (e) show the global distribution at the 300 hPa pressure level, and panels (b), (d), and (e) show zonal means. Note the different scales in each panel.

Black carbon mass concentrations are shown in Fig. 1c and d. The highest BC concentrations occur in the Northern Hemisphere, where the main sources of anthropogenic soot particles, produced from incomplete combustion of fossil fuels, are situated. Additionally, biomass burning is a source of atmospheric BC in remote regions of the Southern Hemisphere (e.g. in Africa and South America). Compared with dust mass concentrations, BC mass concentrations are much lower, with peak values of up to 0.01 µg m⁻³ in the upper troposphere.

Aviation BC is mostly concentrated in the Northern Hemisphere where the majority of the global air traffic is located. The largest concentrations in the upper troposphere at 300 hPa reach values of about 10⁻⁴ µg m⁻³ (Fig. 1e), and the vertical profile shows hotspots for BCair concentrations at the typical flight altitudes (between 200 and 300 hPa) and close to the surface, due to BC emitted in the vicinity of airports (Fig. 1f). Further details on aviation soot in the EMAC-MADE3 model can be found in Righi et al. (2021).

4.2 Glassy organics

In this section, model results concerning the atmospheric dispersion of glassy organic particles are presented. The newly implemented MADE3 tracer glPOM represents organic particles formed from the condensation of natural precursors of organic aerosols, e.g. terpenes (see Sect. 3.2). Emissions occur mainly in regions with strong biogenic activity, e.g. tropical rainforests. Only high-viscosity, glassy particles are considered according to the phase separation depending on the ambient temperature and the glass transition temperature T_g.

The glass transition temperature is strongly influenced by the relative humidity according to Eq. (1), with T_g increasing with decreasing RH. Only for T<T_g can glassy particles occur. This condition is only rarely fulfilled near the surface. The highest mass concentrations (about 0.01 µg m⁻³) are reached at around the 600 hPa niveau (Fig. 2a and b). There, the low ambient temperatures favour the occurrence of the glassy phase. Additionally, dry environments with low RH and, therefore, high T_g lead to favourable conditions for glassy particles, e.g. the northern and southern midlatitudes around 600 hPa in addition to midlatitudes and polar regions in the upper troposphere above 200 hPa (Fig. 2c). This is in agreement with measurements of glassy SOA particles, which have been observed to exist in an amorphous solid state at cirrus temperatures (e.g. Järvinen et al., 2016), while mostly liquid SOA particles have been observed in humid tropical regions (e.g. Bateman et al., 2015).

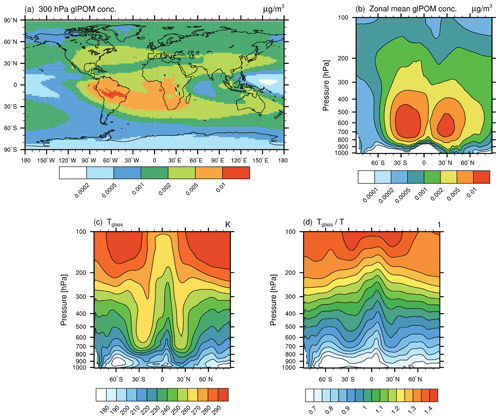
Figure 2 Global distribution of glassy organics (glPOM) at the 300 hPa pressure level (a) and as a zonal mean (b) in micrograms per cubic metre (µg m⁻³), as simulated with EMAC-MADE3. Panels (c) and (d) show the zonally averaged glass transition temperature (T_g) in kelvin (K) and the $T_{\mathrm{g}}/T$ ratio respectively. All panels consider the multi-year average over the simulation period (2010–2019). Note the different scales in each panel.

The $T_{\mathrm{g}}/T$ ratio can be used as an indicator of the particle phase state (Fig. 2d). For $T_{\mathrm{g}}/T\ge \mathrm{1}$, the particle behaves like a solid, whereas $T_{\mathrm{g}}/T<\mathrm{1}$ indicates a semi-solid or liquid state (Shiraiwa et al., 2017). A comparison of the $T_{\mathrm{g}}/T$ ratio with model results from Shiraiwa et al. (2017), also employing the EMAC global model, shows good agreement. Above 500 hPa, almost all SOA particles are transformed into a glassy solid state with $T_{\mathrm{g}}/T$ values above 1. Instead of the simple calculation depending on the relative humidity adopted here, Shiraiwa et al. (2017) employ the organic aerosol submodule ORACLE (Tsimpidi et al., 2014) to simulate the phase state of atmospheric SOA. Our implementation of glPOM in the EMAC-MADE3 model represents a simplified approach to derive a first-order estimate of the highly uncertain climate effects regarding cirrus cloud modifications due to glassy organic INPs. In a sensitivity experiment, we analyse the effect of using different formulations for T_g(RH) (see Sect. 3.2 and Fig. S2). Increased T_g values lead to larger glPOM concentrations mainly at lower altitudes (up to 500 hPa), as conditions favourable for glassy particles are more frequently fulfilled. Above 300 hPa, only small differences in glPOM concentrations are visible.

4.3 Crystalline ammonium sulfate

In this section, model results concerning the newly implemented ammonium sulfate tracer (AmSu) are presented. A detailed description of related calculations and parameterizations of the life cycle of atmospheric ammonium sulfate particles in EMAC-MADE3 is given in Sect. 3.3. AmSu is implemented as a number density tracer and includes a formulation of phase transitions depending on the ambient relative humidity, i.e. only the crystalline phase is represented by this tracer. To analyse the sensitivity of modelled AmSu to different assumptions for its size and composition, different representations of AmSu tracers are used (see Sect. 3.3). AmSu_mixS and AmSu_mixL consider crystalline ammonium sulfate with smaller and larger particle diameters internally mixed with other components, whereas AmSu_ext assumes externally mixed pure ammonium sulfate crystals. Number concentrations of these three AmSu tracers near the surface, at the 300 hPa level, and as zonal-mean vertical distribution are shown in Fig. 3. These results represent averages over the whole simulated time period, which includes cases where ammonium sulfate occurs in its crystalline form as well as cases where the environmental conditions exclude the presence of AmSu crystals and the respective AmSu tracer concentration is, therefore, zero.

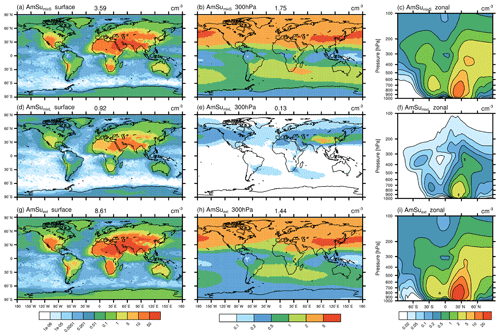
Figure 3 Global distribution of crystalline ammonium sulfate (AmSu) simulated with EMAC-MADE3, considering the multi-year average over the simulation period (2010–2019). Number concentrations per cubic centimetre (cm⁻³) are shown for different AmSu tracers, i.e. AmSu_mixS (a–c), AmSu_mixL (d–f), and AmSu_ext (g–i) respectively. Number concentrations are shown near the surface (a, d, g), at the 300 hPa level (b, e, h), and as zonal means (c, f, i). The numbers above the map plots represent the global averages at that respective pressure level. Note the different scales in each column.

The global patterns are similar for all three AmSu tracers. High number concentrations are simulated at ground level over the continents and in large parts of the middle and upper troposphere. AmSu_mixL shows the lowest concentration values, as these particles have a larger diameter, which leads to lower number concentrations in the mass-to-number conversion of the aerosol mass (Sect. 3.3 and Eq. S6). The largest number concentrations are found for AmSu_ext (above 50 cm⁻³ near the surface). The sum of the AmSu_mixS and AmSu_mixL concentrations is similar to that of AmSu_ext, indicating a low sensitivity to the assumption of internally or externally mixed particles. Therefore, considering only one externally mixed ammonium sulfate tracer could be a reasonable simplification to include crystalline ammonium sulfate in other model systems in order to further elucidate its impacts.

The global dispersion of crystalline ammonium sulfate is strongly related to the concentrations of NH₄ and SO₄ from which it is formed (see Fig. S3, which shows the global distribution of NH₄ and SO₄ mass concentrations). Sources of aerosol sulfate and ammonium are predominantly of anthropogenic origin, e.g. the combustion of sulfur-containing fossil fuels (like coal in power plants or bunker fuels in shipping) or the use of ammoniacal fertilizers respectively and are mostly situated in the Northern Hemisphere (e.g. Feng et al., 2020).

The global distribution of simulated AmSu concentrations is in good agreement with results from other model studies. Wang et al. (2008) analysed the distribution of solid and aqueous sulfate aerosols employing a chemical transport model (Martin et al., 2004; Park et al., 2004) and simulated a global distribution pattern of solid ammonium sulfate particles similar to that shown in Fig. 3. Penner et al. (2018) simulated the aerosol effect on cirrus clouds, including a representation of solid ammonium sulfate in their model, and also found similar global distribution patterns of ammonium sulfate particles to those presented here.

Importantly, the ambient environmental conditions have to fulfil the requirements for ammonium sulfate to reside in the solid phase. Only if the ambient RH is below the efflorescence relative humidity can crystals form. Zonal-mean profiles of RH and ERH are shown in Fig. 4d and e respectively. These quantities are variable in time, i.e. the analysis of multi-year means allows only for rough estimates of the AmSu phase state. ERH is calculated depending on the ammonium-to-sulfate ratio according to Eq. (S4) (see Sect. S1 for details). Upon rehydration, ammonium sulfate crystals remain solid until the deliquescence relative humidity is reached, which is 80 % for ammonium sulfate (Martin, 2000).

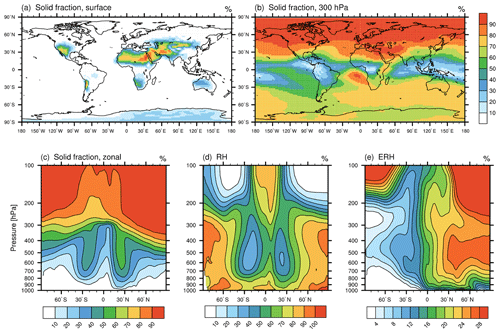
Figure 4 Simulated ammonium sulfate solid fractions in EMAC-MADE3, considering the multi-year average over the simulation period (2010–2019): the fraction of solid ammonium sulfate particles near the surface (a), at 300 hPa (b), and as zonal-mean vertical distribution (c); (d) the zonal-mean relative humidity; and (e) the zonal-mean efflorescence relative humidity. All quantities are dimensionless and are shown as a percentage (%). Note the different scales in panels (d) and (e).

Figure 4a–c show the simulated solid fractions of ammonium sulfate. The solid fractions increase with increasing altitude and show the largest values (close to 100 %) in the upper troposphere of the Northern Hemisphere. As crystallization depends on the ambient relative humidity and the efflorescence relative humidity (see Sect. 3.3), large solid fractions occur in regions with low RH and high ERH (see Fig. 4d and e). The simulated solid fractions shown in Fig. 4 are in good quantitative agreement with results from Wang et al. (2008) and also with Colberg et al. (2003), where a Lagrangian model is employed that calculates trajectories from ECMWF (European Centre for Medium-Range Weather Forecasts) analyses and takes the deliquescence/efflorescence hysteresis of ammonium sulfate into account.

5 Climatology of ice-nucleating particles

In this section, the global distribution of the different INPs simulated with EMAC-MADE3 is presented. Additionally, results concerning the number of pristine, i.e. newly formed, ice crystals from heterogeneous freezing as well as the ice water content (i.e. ice mass per unit mass of air) per heterogeneous freezing mode are shown.

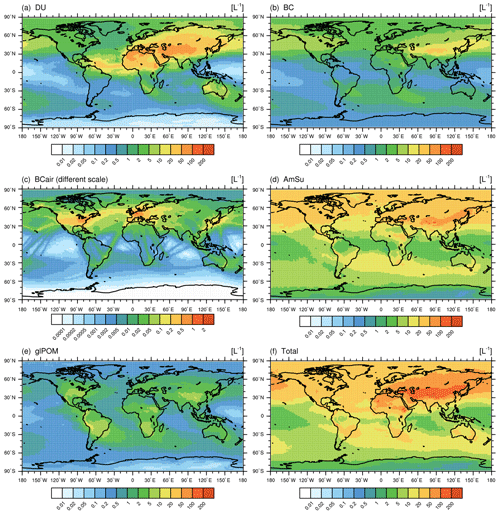
Figure 5 Global distribution of the simulated number concentrations of different INPs per litre (L⁻¹) inside cirrus clouds (selecting only grid boxes with cirrus occurrence) considering the multi-year average over the simulation period (2010–2019) and over all vertical levels. Shown are mineral dust (DU; a), black carbon (BC; b), black carbon from aviation (BCair; c), ammonium sulfate (AmSu; d), glassy organics (glPOM; d), and total INP concentrations (f). Cirrus conditions are selected according to thresholds for simulated ambient temperature (T<238 K) and ice water content (IWC > 0.5 mg kg⁻¹) in every grid box using the 11 h output frequency. The number concentrations of potential INPs (see calculations in Sect. 3.4) are weighted with ice-active fractions (f_act) at ice supersaturations of S_i=1.4, from laboratory measurements (see Table 1). Note the different scale in panel (c).

Global distributions of the number concentrations of the INPs considered in this study (DU, BC, AmSu, glPOM, and BCair) in the cirrus regime are depicted in Fig. 5 in terms of vertically averaged multi-annual means over the years 2010–2019. For this comparison, the number concentrations of potential INPs (calculated as described in Sect. S2) are multiplied by the ice-active fraction (f_act) provided by measurements (see Table 1) in order to obtain the actual concentrations of INPs. Here, values of f_act at a supersaturation ratio with respect to ice of S_i=1.4 are chosen. At such a high S_i value near the homogeneous freezing threshold, all different INP types are able to nucleate ice. This facilitates a direct comparison of INP number concentrations, as possible biases due to different freezing efficiencies are excluded. For this analysis, only grid boxes inside cirrus clouds are considered, which are selected according to thresholds for simulated ambient temperature (T<238 K) and ice water content (IWC > 0.5 mg kg⁻¹), using the original model output frequency of 11 h. The global distribution of the average cirrus cloud occurrence frequency calculated according to these threshold values is shown in Fig. S4. An additional selection criterion is employed to filter out those cases where the crystal size exceeds a certain threshold (R_ice>1000 µm), as such large crystals readily sediment and are removed from the cirrus niveau. This threshold value is chosen according to the analysis of crystal sizes of newly formed ice crystals (see Fig. S5) to include most of the distribution of simulated R_ice values while also excluding very large crystals.

Peak INP number concentrations per species in Fig. 5 reach values of 50 to 100 L⁻¹ for most INP types, while total INP number concentrations show values of up to 200 L⁻¹. Mineral dust INPs are mostly concentrated near strong dust emission regions (e.g. the Sahara or Arabian deserts) as well as in regions of enhanced dust transport (e.g. over the Atlantic Ocean). The BC, BCair, and AmSu INP types show a strong hemispheric gradient with high concentrations in the Northern Hemisphere, as these INPs are strongly related to anthropogenic activities (e.g. combustion of fossil fuels). For the case of BCair, the main aviation flight corridors are clearly visible, which are dominated by air traffic over the northern Atlantic Ocean. BCair number concentrations of up to 2 L⁻¹ are generally smaller compared with other INP types; however, this represents a conservative assumption, and BCair numbers could be larger, as aircraft soot could possibly be pre-activated via processing in contrails (e.g. Mahrt et al., 2018; David et al., 2019; Nichman et al., 2019), whereas the activated fraction of BCair (f_act=0.001) in this work is chosen according to the value for BC. Glassy organic INPs are more homogeneously distributed over the Northern and Southern hemispheres with the highest concentrations (number concentrations mostly around 5 L⁻¹) found over regions of strong biogenic activity (e.g. tropical rainforests), although these concentrations are distinctly smaller compared with most other INP types. As stated earlier, glassy organics as well as crystalline ammonium sulfate INPs only occur under specific conditions, as their phase state depends on the ambient temperature and humidity. Differences in the global distribution of INPs, as seen in Fig. 5, compared with the respective aerosol concentrations shown in the previous sections are a result of the selection of cirrus conditions (i.e. T<238 K, IWC > 0.5 mg kg⁻¹), but they can also be related to the assumptions used for the calculation of INP number concentrations, as described in Sects. 3.4 and S2.

A direct comparison of model results with in situ observations of INP number concentrations in cirrus clouds is challenging, as most measurements were performed at lower altitudes and focused on mixed-phase cloud temperatures. Moreover, in situ measurements of collected particle samples were often performed using diffusion chambers (e.g. Rogers et al., 2001b), where temperatures and supersaturations can be directly controlled but may not correspond to the actual ambient conditions at sample collection, e.g. temperatures below the homogeneous freezing threshold are often difficult to realize. Several studies describe in situ observations of number concentrations of atmospheric INPs, mostly collected at low altitudes and analysed at temperatures above 238 K, ranging from concentrations below 0.1 L⁻¹ to several hundred per litre (e.g. Rogers et al., 1998, 2001a; DeMott et al., 2010; Schrod et al., 2017), in accordance with the INP concentrations simulated here (Fig. 5).

In addition to the global distributions in Fig. 5, a more condensed analysis is presented in Fig. 6a. INP number concentrations for five different latitude regions are shown as a frequency distribution plot. Frequencies are drawn as shaded colours for every INP type and latitude region. Number concentrations of potential INPs are again multiplied by f_act at S_i=1.4, and cirrus conditions are selected according to temperature and ice water content.

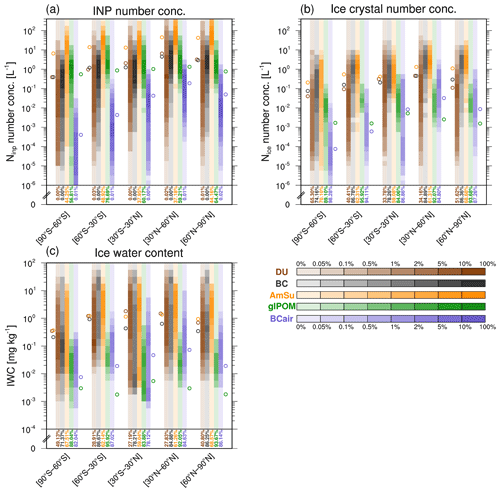
Figure 6 Frequency distributions of (a) simulated INP number concentrations (L⁻¹) as well as (b) number concentrations (N_ice; L⁻¹) and (c)  ice water content (IWC; mg kg⁻¹) of pristine ice crystals inside cirrus clouds per freezing mode for five different latitude regions, calculated from 11 h model output for the simulation period (2010–2019). Shaded colours represent the frequency of occurrence within specific bins for the respective variable considering four logarithmic bins per order of magnitude. The different colours refer to DU (brown), BC (black), AmSu (orange), glPOM (green), and BCair (purple). Frequencies in the bottom bin, including all values down to zero, are depicted as coloured text. Cirrus conditions are selected according to temperature (T<238 K) and ice water content (IWC > 0.5 mg kg⁻¹) in every model grid box and time step. Additionally, only grid boxes without ice formation on pre-existing ice crystals are selected ($N_{\mathrm{preex}}<{\mathrm{10}}^{-\mathrm{23}}$ L⁻¹). The number concentrations of potential INPs are weighted with ice-active fractions from laboratory measurements (f_act at S_i=1.4; see Table 1). Open circles to the left and right of every latitude region denote mean values for the different INP species.

All INP types except glPOM show a marked difference between the Northern and Southern hemispheres, with the highest concentrations at the northern latitudes. BC, BCair, and AmSu are mostly concentrated in the region of 30–60^∘ N, as anthropogenic influences and emissions play a key role for these INP types. Aircraft BC has notable concentrations almost only in this region, with concentrations in the range from 10⁻³ to 1 L⁻¹ showing the highest occurrence frequencies. In other regions, BCair concentrations are generally much lower than those of other INP types. Non-aircraft BC INPs frequently reach concentrations of up to 10 L⁻¹ in those regions. AmSu INPs can show high concentrations of up to 100 L⁻¹, exceeding other INP concentrations in most cases. However, in many other cases, AmSu concentrations are very low or zero (bottom bins occurring with probabilities of up to 49 %). These are mainly related to ambient conditions under which ammonium sulfate does not occur in its crystalline state. Mineral dust INPs occur most frequently in the latitude region around the Equator and 30–60^∘ N, where dominant dust emission regions are situated (e.g. the Sahara, Arabian, and Asian deserts). Glassy organic INPs are more evenly distributed over all latitudes, with concentrations mostly below 5 L⁻¹ (lower values compared with most other INP types). Similar to AmSu, ambient conditions often do not favour the glassy state, which leads to large occurrence frequencies in the lowest concentration bin (up to 77 %). Additionally, we analyse the INP number concentrations for the three different representations of glass transition temperatures T_g(RH), considering the different SOA proxies citric acid, glucose, and sucrose respectively (see Fig. S6). Using different T_g representations results in an additional uncertainty in glPOM INP number concentrations of up to 1 order of magnitude. Differences are largest between the SOA proxies citric acid and glucose but only slight between glucose and sucrose. Notably, the freezing efficiency of crystalline ammonium sulfate and glassy organic INPs is still uncertain, as only few laboratory studies have investigated their ice-nucleating abilities. A lower ice-nucleating ability of crystalline ammonium sulfate, e.g. due to coatings of organic material (Ladino et al., 2014; Bertozzi et al., 2021), would reduce the impact of ammonium sulfate INPs. However, due to the large number of crystalline ammonium sulfate particles simulated here, they would probably still contribute a substantial fraction to the total INP number in large parts of the globe.

Figures 5 and 6a can help to identify regions on the globe where different INP types are likely to compete with each other for the available supersaturated water vapour during the freezing process. In the Southern Hemisphere, competition between ammonium sulfate and glassy organics is possible, as these INPs are highly concentrated in southern regions, whereas other INP types show low concentrations. The northern Atlantic is a possible competition region between AmSu, BC, and BCair INPs. Over most regions in Central Asia, several different INP types (DU, BC, and AmSu) are present in relatively similar concentrations, leading to possible competition mechanisms between these INPs.

By coupling the different INP types to the microphysical cirrus cloud scheme, their ice nucleation potential under cirrus conditions can be analysed, including possible competition mechanisms between different INPs. Similar to INP concentrations, we show the number concentrations of pristine ice crystals formed via heterogeneous freezing induced by INPs and the corresponding ice water content (i.e. cloud ice mass per unit mass of air) in Fig. 6b and c for each heterogeneous freezing mode. The analysis of these quantities allows for an evaluation of the relative importance of the different INP types in heterogeneous ice formation. Concentrations of newly formed ice crystals from the different freezing modes (Fig. 6b) are generally lower than INP number concentrations (on average about 1–2 orders of magnitude). Additionally, very small values (bottom bins in Fig. 6b) occur much more frequently. This clearly shows that only a fraction of the number of INPs actually nucleates and forms ice crystals. Importantly, the bottom bins (i.e. very small values) for ice crystals from mineral dust freezing often show much lower frequencies compared with the other freezing modes. This indicates a pronounced competition mechanism between the different INPs. The most efficient INPs, i.e. mineral dust and ammonium sulfate, rapidly deplete the available supersaturated water vapour and inhibit freezing induced by less ice-active INP types.

In addition to N_ice from heterogeneous freezing modes, the number concentrations of homogeneously formed ice crystals are shown in Fig. 7. In all latitude regions, these are much larger than concentrations of heterogeneously formed ice crystals (up to 3–4 orders of magnitude). Occurrence frequencies in the lowest concentration bin are often very large (78 %–97 %), indicating that heterogeneous freezing often prevents homogeneous ice nucleation. However, in those cases where homogeneous freezing takes place, it produces very large concentrations of ice crystals. This process has also been described in detail in publications such as Kärcher and Lohmann (2002) and Kärcher et al. (2006). The extent of this attenuation effect and the resulting cirrus and climate modifications have been shown recently for the case of the aviation soot–cirrus effect (Righi et al., 2021).

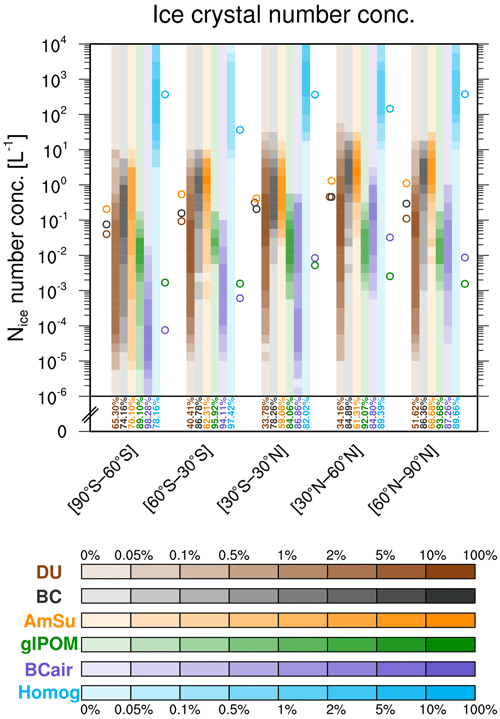
Figure 7 As in Fig. 6b but additionally showing the frequency distribution of pristine ice crystals formed by homogeneous freezing (light blue).

Figure 6c shows the ice water content for each heterogeneous freezing mode. The IWC of pristine ice crystals indicates how much ice mass accumulates on INPs during the freezing process, regarding the nucleation and growth of these crystals during the first model time step of the existence of the respective cirrus cloud. INPs with a high freezing efficiency initiate nucleation at relatively low ice supersaturations, resulting in ice crystals growing to larger sizes during the freezing process. Here, the highly efficient INPs, i.e. mineral dust and ammonium sulfate, often dominate the IWC in several regions, with average values up to 2 mg kg⁻¹, and often show lower frequencies in the lowest concentration bin compared with the other INP types. This indicates the large importance of these two INP types. Especially the strong impact of crystalline ammonium sulfate INPs is remarkable, as several previous studies have reported mineral dust as the single most important INP type (e.g. Cziczo et al., 2013; Froyd et al., 2022). This implies the need for dedicated measurements of the ice nucleation of ammonium sulfate in the cirrus regime. Additionally, future modelling efforts should take crystalline ammonium sulfate into account to further evaluate its importance for aerosol-induced cirrus formation.

To evaluate the quality of the simulated INP numbers, they can be compared with in situ observations that, however, mostly focused on the mixed-phase temperature regime. Rogers et al. (1998) described aircraft measurements performed over North America at high altitudes (around 10 km) but analysed samples at temperatures mostly above 243 K in a flow diffusion chamber. They reported INP concentrations between ∼0.1 and 500 L⁻¹, with larger concentrations at lower temperatures and higher supersaturations. This agrees well with our model results obtained for that region (Fig. 5f). Additionally, Rogers et al. (2001a) analysed aircraft measurements conducted in the Arctic for temperatures between 263 and 243 K and humidities ranging from ice saturation to water supersaturation. They observed an average INP concentration of 16 L⁻¹ with rare very high concentration values (hundreds of INPs per litre). This is in good accordance with the simulated INP concentrations of around 20 L⁻¹ in the region of 60–90^∘ N. DeMott et al. (2010) presented a parametrization of INP concentrations using a combination of data from several different aircraft campaigns. Measurements were mostly performed for temperatures above 239 K where INP concentrations ranging from 0.1 to 100 L⁻¹ were observed, which corresponds to the range of simulated values shown in Fig. 6a. Jensen et al. (2010, 2013) focused on cirrus clouds in the tropical tropopause layer, and they predicted that measured ice crystal numbers and cloud optical properties are in accordance with INP concentrations below 20 L⁻¹. This is in agreement with our model results in the equatorial region presented here (Figs. 5, 6a). Additionally, Schrod et al. (2017) presented measurements performed with un-piloted aircraft systems over the eastern Mediterranean at altitudes below 2.5 km and reported INP peak concentrations of above 100 L⁻¹ at 243 K, also confirming the model results presented in Fig. 5f.

In addition to observations, other global model studies have been performed to analyse the distribution of ice-nucleating particles on the globe. Barahona et al. (2010) carried out simulations with the NASA Global Modeling Initiative chemical and transport model (Rotman et al., 2001; Liu et al., 2007), coupled to an analytical ice microphysics parametrization, considering DU, BC, and glassy organics as heterogeneous freezing nuclei. Their results show INP concentrations mostly around 5 L⁻¹ in the equatorial region, which is in accordance with the results presented here (Fig. 6a). Hendricks et al. (2011) performed a similar study to analyse the effect of INPs on cirrus clouds employing the ECHAM4 general circulation model (Roeckner et al., 1996), considering heterogeneous freezing on DU and BC in addition to homogeneous freezing. They report modelled ice crystal number concentrations formed via heterogeneous freezing of between 0.01 and 0.1 L⁻¹, in agreement with the range of N_ice values described in this section (Fig. 6b). However, N_ice from BC freezing in Hendricks et al. (2011) is about 10 times lower compared with the dust freezing mode. This difference between DU and BC is not visible in the results presented here. Disparities with respect to Hendricks et al. (2011) could be due to differences in the representation of the atmospheric aerosol, the parametrization of the freezing processes, and different model dynamics due to the use of nudging.

6 Conclusions

In this paper, we present a global climatology of ice-nucleating particles by analysing global model simulations performed with EMAC-MADE3. This climatology comprises the main currently discussed INP types under cirrus conditions. Despite mineral dust and black carbon particles, which have generally been considered to be INPs in many previous model studies, we additionally include crystalline ammonium sulfate and glassy organic INPs. These two novel INP species have only rarely been considered in global models, despite several laboratory studies suggesting their pronounced ice-nucleating potential. Hence, their climate impact on a global scale is still highly uncertain.

We present atmospheric distributions of mineral dust and black carbon, including black carbon from aviation emissions, as also analysed and evaluated in previous studies with EMAC-MADE3 (Beer et al., 2020; Righi et al., 2021). In addition, we describe the implementation of phase transitions of ammonium sulfate and organic particles in detail. The formulation of the phase state is very important for these particles, as only the crystalline phase of ammonium sulfate and the glassy phase of organic particles induce heterogeneous ice nucleation. We present the atmospheric distributions of crystalline ammonium sulfate and glassy organics and compare their respective atmospheric concentrations with results from previous model studies, showing overall good agreement with the results presented here.

We calculate the concentrations of potential ice-nucleating particles from the simulated aerosol concentrations according to the scheme described in Righi et al. (2020), which is adapted to include the additional INP types, i.e. crystalline ammonium sulfate and glassy organics. We present and analyse the resulting multi-annual mean climatology of INPs under cirrus formation conditions. Simulated INP number concentrations, in the range of about 1 to 100  L⁻¹, agree well with in situ observations (e.g. Rogers et al., 1998, 2001a; DeMott et al., 2010; Schrod et al., 2017) and other global model studies (e.g. Barahona et al., 2010; Hendricks et al., 2011).

High dust INP concentrations (about 100 L⁻¹) are simulated over dust-dominated regions (e.g. the Sahara, Arabian, and Asian deserts). Black carbon and ammonium sulfate INPs show a distinct north–south gradient with the largest concentrations in the Northern Hemisphere (up to 50 and 100 L⁻¹ respectively), probably dominated by anthropogenic influences. Importantly, crystalline ammonium sulfate INP concentrations are comparable to or even exceed those of mineral dust in large parts of the globe, e.g. the Southern Hemisphere and the high northern latitudes. Glassy organic INPs are concentrated in regions with strong biogenic activity, mainly in the tropics and in the Southern Hemisphere, but they often have much lower concentrations compared with most other INP types, i.e. below 10 L⁻¹. The mean values for glassy organics and for ammonium sulfate, however, also include cases where these INPs are not glassy or crystalline respectively, and larger concentrations are possible at specific times and locations. Aviation soot INPs show highest concentrations along typical aircraft flight routes, mainly between Europe and North America (about 1 L⁻¹).

By coupling the different INP types to the microphysical cirrus cloud scheme, their ice nucleation potential under cirrus conditions is analysed, including possible competition mechanisms between different INPs and considering regional, latitude-specific differences. Concentrations of freshly nucleated pristine ice crystals from heterogeneous freezing are typically 1–2 orders of magnitude lower than respective INP number concentrations. In many cases, only a fraction of the available INPs can be activated due to low cooling rates. Owing to the comparably small number concentrations of INPs, the mean number concentrations of INP-induced ice crystals are also much lower than those of homogeneously formed crystals (up to 3–4 orders of magnitude). The most abundant INP types, e.g. soot, dust, and ammonium sulfate, often show the largest impact on the ice crystal number concentration of freshly nucleated crystals. The different INP species compete with each other for the available supersaturated water vapour. The most efficient INPs, i.e. mineral dust and ammonium sulfate, inhibit freezing induced by less ice-active INP types in many cases, leading to frequently occurring very low pristine ice crystal concentrations for (aviation) soot and glassy organic INPs. The highly efficient dust and ammonium sulfate INPs also generate the largest ice mass and show a marked effect on the ice water content.

To conclude, the climatology of ice-nucleating particles at cirrus formation presented in this study demonstrates the importance of including crystalline ammonium sulfate along with mineral dust and soot particles in global models. Glassy organic particles probably have only minor influences, as their INP concentrations in the upper troposphere are mostly small. The remarkable large importance of crystalline ammonium sulfate shown here should be further investigated in dedicated observation campaigns and modelling efforts.

The described results concerning INPs and their interaction with cirrus clouds are still subject to uncertainties. Most notably, the cloud microphysics scheme mainly relies on calculations for the whole model grid box. Subgrid-scale processes are parameterized, e.g. the variability in the vertical velocity or the sedimentation of ice crystals (including the removal of embedded INPs; Kuebbeler et al., 2014; Righi et al., 2020). However, these parameterizations are limited and introduce additional uncertainties, which could lead to a misrepresentation of the impact of heterogeneous ice nucleation pathways. Additionally, the presented results are dependent on the freezing efficiency of the different INPs. For instance, Righi et al. (2021), employing a similar model set-up, found a strong dependency of the aviation soot–cirrus effect on the assumed ice-nucleating properties of soot particles. This uncertainty could be further analysed in future studies by varying the ice nucleation thresholds of the different INPs.

The new insights achieved in the present study could be further deepened by additional model developments and analyses. Recent laboratory studies have identified yet another type of ice-nucleating particle under cirrus conditions, i.e. marine aerosol (e.g. Wilbourn et al., 2020; Wagner et al., 2021). Potential influences of these marine particles on cirrus clouds could be evaluated by including them as INPs in the cirrus ice nucleation scheme. Additionally, the analysis of the simulated global distribution of different INPs could be further refined by applying machine learning clustering algorithms (e.g. k-means clustering; Hartigan and Wong, 1979) to identify regions dominated by specific INP types or by possible competition mechanisms between different INPs. This technique has recently been demonstrated for the analysis of global aerosol simulations by Li et al. (2022). Following the results presented in this study, cirrus cloud and the resulting climate modifications induced by the ice-nucleating particles described here could be analysed in order to provide further insight into these INP-induced climate effects.