Technical note: Frenkel, Halsey and Hill analysis of water on clay minerals: toward closure between cloud condensation nuclei activity and water adsorption

Insoluble atmospheric aerosol, such as mineral dust, has been identified as an important contributor to the cloud droplet number concentration and indirect climate effect. However, empirically derived Frenkel–Halsey–Hill (FHH) water adsorption parameters remain the largest source of uncertainty in assessing the effect of insoluble aerosol on climate using the FHH activation theory (FHH-AT). Furthermore, previously reported FHH water adsorption parameters for illite and montmorillonite determined from water adsorption measurements below 100 % RH do not satisfactorily agree with values determined from FHH-AT analysis of experimental cloud condensation nuclei (CCN) measurements under supersaturated conditions. The work reported here uses previously reported experimental water adsorption measurements for illite and montmorillonite clays (Hatch et al., 2012, 2014) to show that improved analysis methods that account for the surface microstructure are necessary to obtain better agreement of FHH parameters between water adsorption and experimental CCN-derived FHH parameters.

1 Introduction

By mass, mineral dust is the most abundant type of aerosol in the Earth's atmosphere. The estimated average atmospheric loading of mineral dust aerosol is 19.2 Tg, nearly 63 % of the total aerosol burden (Textor et al., 2006). Entrained minerals are intricately linked to climate and the hydrological cycle and have a significant impact on air quality, visibility, and health (Creamean et al., 2013; Cwiertny et al., 2008; Karanasiou et al., 2012; Mahowald et al., 2007; Prospero and Lamb, 2003; Zhu et al., 2011). The Earth's energy budget is altered due to mineral dust aerosol effects on the radiative balance of the Earth and cloud formation and lifetime (Stevens and Feingold, 2009). Nearly all (75 % to 100 %) atmospheric mineral dust emitted into the atmosphere is expected to be relatively bare minerals from arid or semiarid source regions, not internally mixed with organic components (Forster et al., 2007; Ginoux et al., 2012). Until recently, these bare, insoluble mineral dust particles' influence on warm cloud formation has been assumed to be negligible from the lack of soluble material present (Manktelow et al., 2010; Pringle et al., 2010). However, many studies have shown that bare dust can be active cloud condensation nuclei (CCN), even if it is only weakly hygroscopic (Herich et al., 2009; Koehler et al., 2009) as CCN activity is driven by pre-adsorbed water multilayers on the surface under sub-saturated water vapor conditions (Kumar et al., 2009a, b; Sorjamaa and Laaksonen, 2007). Recent advances have led to an increased understanding of the role of adsorbed water on CCN activation of insoluble aerosols (Laaksonen, 2015; Laaksonen et al., 2016; Sorjamaa and Laaksonen, 2007) and regional and global models are beginning to explore their effects on climate and precipitation (Karydis et al., 2011, 2012; Smoydzin et al., 2012).

Much effort has been invested in parameterizing the contribution of insoluble mineral aerosol to the number of available CCN and cloud droplets in the atmosphere. Most notable is the recent development of the Frenkel–Halsey–Hill adsorption activation theory (FHH-AT) (Kumar et al., 2009a, b; Sorjamaa and Laaksonen, 2007). The FHH-AT framework was developed to account for the effect of adsorbed water multilayers on the CCN activity of wettable, insoluble aerosol and is based on two competing physical phenomena: the Kelvin effect and multilayer water adsorption. Since its inception, FHH-AT has been substantiated based on water adsorption, hygroscopicity, and CCN measurements of mimicked freshly emitted mineral dust aerosol (Hatch et al., 2014; Kumar et al., 2009a, 2011a, b). Additionally, recent modeling studies have incorporated the FHH-AT framework to investigate global and regional impacts of mineral dust aerosol on cloud formation (Bangert et al., 2012; Karydis et al., 2011, 2012). Karydis et al. (2011) incorporated FHH-AT into the NASA Global Monitoring Initiative chemical transport model and found that insoluble mineral aerosol contributes up to 40 % of the annual averaged CCN and 23 % of the annual averaged cloud droplet number concentration (CDNC) in cloud-forming areas. Furthermore, dust hydrophilicity, expressed via Frenkel–Halsey–Hill (FHH) adsorption theory parameters, appears to have a more significant impact on the CDNC than dust concentration (Karydis et al., 2012). However, sensitivity studies have indicated that uncertainties in experimentally determined FHH water adsorption parameters (A_FHH and B_FHH) could modulate the relative contribution of mineral aerosol to cloud droplet number by up to 56 % (Karydis et al., 2011). Thus, the accuracy of FHH-AT parameters affects the ability of atmospheric models to predict indirect climate effects of mineral aerosol, one of the least understood factors contributing to climate change (IPCC, 2013).

2 Background

Implementation of FHH-AT in climate models relies on the empirical measurement of FHH adsorption parameters obtained by applying the FHH adsorption model to experimental water adsorption measurements. The FHH adsorption isotherm describes multilayer water adsorption, assuming an adsorption potential gradient based on the distance of the adsorbed water layer from the particle surface and is described by Eq. (1) (Hill, 1952):

$$\begin{array}{}\text{(1)}& s=\exp \left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right),\end{array}$$

where s is the saturation ratio of water vapor above the sample, θ is the relative water coverage (or number of adsorbed monomolecular water layers), and A_FHH and B_FHH are FHH empirical fit parameters that describe the intermolecular interactions governing the adsorption potential. A_FHH characterizes interactions between the surface and first adsorbed water layer as well as interactions between adjacent molecules and thus governs the overall extent of water coverage. Higher A_FHH values suggest that more water can be adsorbed. B_FHH describes the interactions between the surface and subsequent adsorbate layers. Smaller B_FHH values characterize stronger attractive forces over greater distances from the surface. Thus, B_FHH greatly influences the shape of the adsorption isotherm, particularly at high saturation ratios. As a result, CCN activation determined using FHH-AT is predominantly driven by the magnitude of B_FHH (Kumar et al., 2009a). In order to accurately determine A_FHH and B_FHH, experimental measurements of θ as a function of relative humidity (RH) must be known to a high degree of accuracy.

FHH-AT describes the contribution of water adsorption to CCN activity by Eq. (2) (Hung et al., 2015; Kumar et al., 2009b; Sorjamaa and Laaksonen, 2007; Tang et al., 2016).

$$\begin{array}{}\text{(2)}& s=\exp \left(-A_{\mathrm{FHH}}{\mathit{\theta }}^{-B_{\mathrm{FHH}}}\right)\exp \left({\displaystyle \frac{\mathrm{4}\mathit{\sigma }{M}_{\mathrm{w}}}{RT{\mathit{\rho }}_w{D}_{\mathrm{p}}}}\right)\end{array}$$

The first exponential term represents the effect of water adsorption in the form of the FHH adsorption model. The second exponential term represents the Kelvin effect, where σ is the surface tension of water ($\mathrm{7.20}\times {\mathrm{10}}^{-\mathrm{2}}$ J m⁻²) (Pruppacher and Klett, 1980), M_w is the molar weight of water, R is the universal gas constant, T is the temperature, and ρ_w is the water density. Equation (2) can be used to calculate CCN activity under supersaturated water vapor conditions if A_FHH and B_FHH are known based on fitting Eq. (1) to experimental water adsorption measurements under sub-saturated water vapor conditions (Hatch et al., 2014; Hung et al., 2015). Alternatively, A_FHH and B_FHH can be determined from size-resolved experimental CCN activation measurements of the critical supersaturation, s_c, as a function of the dry particle diameter, D_dry (Kumar et al., 2011a, b; Sorjamaa and Laaksonen, 2007).

Recent studies have attempted to calculate CCN activities of mineral dust components based on FHH parameters derived from experimental water adsorption parameters (Hatch et al., 2014; Hung et al., 2015). Hatch et al. (2014) found that while the calculated CCN activation was in good agreement with experimental CCN measurements of similar minerals (illite and montmorillonite clay) (Kumar et al., 2011a, b), the FHH adsorption parameters were significantly different based on the method by which they were acquired: experimental water adsorption (Hatch et al., 2014) vs. aerosol CCN activation measurements (Kumar et al., 2011a, b; Tang et al., 2016). Figure 1 shows the previously reported experimental water adsorption isotherms for (a) illite and (b) montmorillonite clays based on water adsorption measurements (Hatch et al., 2014). For comparison, Fig. 1 also shows the FHH adsorption isotherms of illite and montmorillonite based on A_FHH and B_FHH parameters derived from FHH-AT analysis of size-selected CCN measurements using wet (Kumar et al., 2011b) or dry (Kumar et al., 2011a) aerosol generation methods. The FHH adsorption isotherms from CCN activation measurements (dashed lines) were calculated based on reported (Kumar et al., 2011a, b) A_FHH and B_FHH values using Eq. (3) (Tang et al., 2016).

$$\begin{array}{}\text{(3)}& \mathit{\theta }=\sqrt[B_{\mathrm{FH}}]{{\displaystyle \frac{A_{\mathrm{FHH}}}{-\ln \left(s\right)}}}\end{array}$$

As shown in Fig. 1, the relative water coverage based on water adsorption measurements differs by a factor of 5 (illite) and 10 (montmorillonite) at 40 % RH from the adsorption curves calculated using FHH parameters derived from aerosol CCN activation measurements. The work presented here aims to address potential sources of the outstanding differences between FHH parameters obtained from water adsorption (Hatch et al., 2014) and CCN activation (Kumar et al., 2011a, b) measurements of illite and montmorillonite clays. Previously reported experimental water adsorption measurements on montmorillonite and illite clays by Hatch et al. (2012) are used to show that improved analysis methods accounting for surface microstructure are necessary to obtain more accurate FHH adsorption parameters from water adsorption measurements and better agreement to experimental CCN-derived FHH parameters.

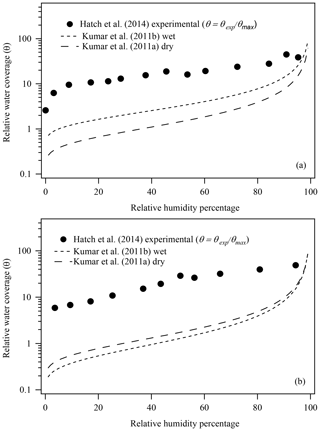
Figure 1 Comparison of previously reported experimental water adsorption isotherms ($\mathit{\theta }={\mathit{\theta }}_{\exp }/{\mathit{\theta }}_{\max }$) and FHH adsorption isotherms from FHH parameters determined from size-selected CCN measurements of (a) illite and (b) montmorillonite aerosol generated using wet or dry aerosol generation methods (Hatch et al., 2014; Kumar et al., 2011a, b).

3 FHH activation theory water adsorption analysis

The results discussed here are based on further assessment of experimental water adsorption measurements previously reported in the literature (Hatch et al., 2012, 2014). Hatch et al. (2012, 2014) reported water adsorption measurements on montmorillonite (SWy-2) and illite (IMt-1) clays obtained from the Clay Minerals Society's Source Clays Repository. Water adsorption was measured using a horizontal attenuated total reflectance Fourier transform infrared (HATR-FTIR) spectrometer with a humidified flow reactor. Details of experimental procedures and adsorbed water quantification can be found in the literature (Hatch et al., 2012, 2014). Water content as a function of RH was reported as a mass ratio of adsorbed water to dry mineral sample mass, $m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}/m_{\mathrm{sample}}$ (in $g_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}/g_{\mathrm{sample}})$, and was found to be in excellent agreement with previous gravimetric water content measurements on the same clays (Hatch et al., 2012; Schuttlefield et al., 2007b).

Traditionally, water content reported as $m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}/m_{\mathrm{sample}}$ is used to determine the relative surface coverage (θ) by first converting the mass ratio to an experimental coverage, θ_exp (molec. cm⁻²), using Eq. (4) (Tang et al., 2016).

$$\begin{array}{}\text{(4)}& {\mathit{\theta }}_{\exp }={\displaystyle \frac{m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{m_{\mathrm{sample}}}}{\displaystyle \frac{N_{\mathrm{A}}}{M_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{A}_{\mathrm{BET}}}},\end{array}$$

where N_A is Avogadro's number, $M_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is the molar mass of water, and A_BET is the BET surface area using N₂ as the adsorbate. The relative surface coverage is then determined by dividing θ_exp by a maximum coverage, θ_max, or the maximum number of water molecules per centimeter squared that can be adsorbed to form a complete monolayer (ML) on the mineral surface. θ_max is often approximated as 1×10¹⁵ molec. cm⁻² or the inverse of the cross-sectional area of a water molecule, 1∕πr², where r is the radius of a water molecule. This method for obtaining θ from the experimental mass ratio of adsorbed water has been used in previous studies (Hatch et al., 2014; Hudson et al., 2002; Schuttlefield et al., 2007a, b) and was recommended as the preferred technique in a recent review paper (Tang et al., 2016). However, obtaining θ in this way is based on assumptions that are not relevant to the systems studied and could introduce large uncertainties. For example, the water molecule is assumed to be spherical on a molecular scale. More significantly, θ_max is calculated assuming a flat surface. That is, θ_max represents the maximum number of spherical water molecules that can fit on a flat surface of 1 cm². However, atmospheric mineral dust particles are widely known to exhibit significant surface microstructure and porosity, leading to a significantly larger surface area than that of a flat surface. Thus, the above method for obtaining θ from a mass ratio of adsorbed water can significantly overestimate θ, leading to erroneous FHH adsorption parameters upon fitting the FHH adsorption model to experimental water adsorption isotherms. The estimated θ_max is expected to account, at least in part, for differences in FHH parameters and adsorption isotherms obtained from water adsorption and CCN activation measurements (Fig. 1).

More accurate θ values that account for the surface microstructure of the clay particles can be determined if the maximum ML water coverage is directly determined from experimental water adsorption data. The Brunauer–Emmett–Teller (BET) adsorption model is commonly applied to multilayer adsorption isotherms to determine a sample's specific surface area based on the amount (in volume) of adsorbate necessary to achieve ML coverage and the size of the adsorbate molecule. Equation (5) shows the linear form of the BET model (Brunauer et al., 1938).

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\frac{P}{P_o}}{\left(\mathrm{1}-\frac{P}{P_o}\right)V}}={\displaystyle \frac{\mathrm{1}}{V_{m^C}}}+{\displaystyle \frac{\left(c-\mathrm{1}\right)}{V_{m^C}}}\left({\displaystyle \frac{P}{P_o}}\right)\end{array}$$

In Eq. (5), $\frac{P}{P_o}$ represents RH, V is the measured volume (cm³) of surface adsorbed water, V_m is the volume (cm³) of water necessary to achieve ML coverage, and c is a constant that is related to the enthalpy of adsorption for any layer of adsorbed water. V_m and c can be determined by fitting experimental adsorption isotherms with Eq. (5) (Brunauer et al., 1938; Hatch et al., 2012). Since V_m is the volume equivalent of θ_max, the relative surface coverage can be determined by $\mathit{\theta }=V/V_m$ as in Hung et al. (2015). BET analysis of water adsorption on illite and montmorillonite clays showed that ML water adsorption occurs at 0.06₅±0.03₂ and 0.06₃±0.03₆ g${}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}/g_{\mathrm{sample}}$, respectively (Hatch et al., 2012). The volume of adsorbed water necessary to achieve ML coverage can be calculated from these ML water content values expressed as mass ratios (Hatch et al., 2012) following Eq. (6).

$$\begin{array}{}\text{(6)}& V={\displaystyle \frac{m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{m_{\mathrm{sample}}}}{\displaystyle \frac{m_{\mathrm{sample}}}{D_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}\end{array}$$

In Eq. (6), m_sample is the mass (g) of sample, $\frac{m_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{m_{\mathrm{sample}}}$ represents the experimental mass ratio of adsorbed water ($g_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}/g_{\mathrm{sample}}$), and $D_{{\mathrm{H}}_{\mathrm{2}}\mathrm{0}}$ is the density of water at room temperature (997.045 kg m⁻³) (Lide, 1995). Given illite and montmorillonite sample masses of 0.8 and 0.3 mg, V_m is calculated, to be $\mathrm{5.2}\times {\mathrm{10}}^{-\mathrm{5}}$ and $\mathrm{1.9}\times {\mathrm{10}}^{-\mathrm{5}}$ cm³, respectively, based on BET analysis of experimental water adsorption data (Hatch et al., 2012).

For comparison, V_m based on the estimated θ_maxvalue of 1×10¹⁵ molec. cm⁻² can be calculated using Eq. (7).

$$\begin{array}{}\text{(7)}& \mathrm{Estimated}{V}_m={\displaystyle \frac{{\mathit{\theta }}_{\max }{M}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{A}_{\mathrm{BET}}{m}_{\mathrm{sample}}}{N_A{D}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}\end{array}$$

In Eq. (7), $M_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is in kilograms per mole (kg mol⁻¹), $D_{{\mathrm{H}}_{\mathrm{2}}\mathrm{0}}$ is in kilograms per cubic centimeter (kg cm⁻³), and A_BET (using N₂ as an adsorbate) is in centimeters squared per gram (cm² g⁻¹) (Hatch et al., 2012). A θ_max of 1×10¹⁵ molec. cm⁻² is equivalent to V_m values of $\mathrm{5.0}\times {\mathrm{10}}^{-\mathrm{6}}$ and $\mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{6}}$ cm³ water for illite and montmorillonite clays, respectively. This is approximately an order of magnitude less adsorbed water at ML coverage than V_m values directly determined from experimental water adsorption data using BET analysis. Thus, previous studies that use θ_max to calculate θ are overestimating the relative water coverage by up to an order of magnitude. This result is consistent with discrepancies in FHH curves determined based on previous water adsorption and CCN activation measurements illustrated in Fig. 1 and thus is likely to be a major source of the disagreement observed in the literature.

Using Eq. (6), V and θ, where $\mathit{\theta }=V/V_m$, were determined as a function of the relative humidity percentage based on previously reported water content mass ratios for illite and montmorillonite clays (Hatch et al., 2012). Figure 2 shows the calculated θ for (a) illite and (b) montmorillonite as a function of the relative humidity percentage based on obtaining V_m from BET analysis of experimental water adsorption data (Hatch et al., 2012). For comparison, adsorption curves calculated using Eq. (1) based on A_FHH and B_FHH parameters derived from CCN activation measurements of dry-generated illite and montmorillonite are also shown (Kumar et al., 2011a, b). In contrast to Fig. 1, which shows θ as calculated using the estimated θ_max, Fig. 2 demonstrates that direct measurement of ML water content using BET analysis of the experimental data significantly enhances closure between adsorption isotherms derived from water adsorption and CCN activation measurements of microstructured clay minerals. As shown, the experimental adsorption curves of θ as a function of the relative humidity percentage are now in much better agreement with FHH adsorption curves based on FHH parameters from dry-generated illite and montmorillonite clay minerals, thus reducing the disagreement between these two methods (Hatch et al., 2014; Kumar et al., 2011a, b; Laaksonen et al., 2016; Tang et al., 2016).

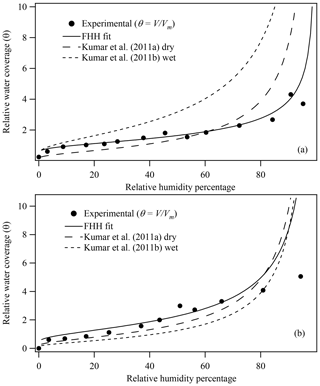
Figure 2 (a) Illite and (b) montmorillonite experimental water adsorption isotherms (Hatch et al., 2012) and associated FHH fit based on constrained FHH analysis, where the experimental θ was calculated as V∕V_m and V_m was determined from BET analysis of adsorption isotherms. FHH adsorption isotherms from FHH parameters determined from size-selected CCN measurements of aerosol generated using wet or dry aerosol generation methods are also shown (Kumar et al., 2011a).

To obtain more accurate FHH adsorption parameters from the experimental water adsorption data for illite and montmorillonite clays shown in Fig. 2, Eq. (1) was rearranged to a linear relationship as shown in Eq. (8) (Tang et al., 2016).

$$\begin{array}{}\text{(8)}& \ln [-\ln (s\left)\right]=\ln A_{\mathrm{FHH}}-B_{\mathrm{FHH}}\ln \mathit{\theta }\end{array}$$

Linear regression analysis of ln[−ln (s)] as a function of ln θ from 40 %–90 % RH allows for the determination of A_FHH and B_FHH (Hung et al., 2015; Tang et al., 2016). According to Hung et al. (2015), constraining the FHH adsorption model fit to a limited range of high RH values avoids uncertainties due to assumptions inherent in the FHH adsorption theory, as the fit should be limited to the multilayer water adsorption regime. Importantly, the FHH adsorption model assumes that particles are spherical, of a single universal diameter, and have a smooth surface and that water is uniformly distributed (Hill, 1952). These assumptions are problematic when applied to adsorption measurements on bulk, polydisperse mineral dust particles which are known to be irregularly shaped and porous. Constraining the fit to higher RH values helps avoid surface porosity effects on the resulting FHH adsorption parameters. However, swelling clay minerals, such as montmorillonite, are problematic as the multilayer adsorption regime begins at higher RH values. For example, previous studies have shown that the multilayer adsorption regime begins at ∼70 % RH for montmorillonite clay (Cases et al., 1992; Mooney et al., 1952), and thus the FHH fit should be constrained from 70 % to 90 % RH. Unfortunately, the limited number of data at high RH values precludes the feasibility of fitting the FHH model over this smaller range of RH values. Thus, the FHH fit parameters reported here for montmorillonite suffer from uncertainty due to the swelling action of smectite clays.

Figure 3 shows the FHH adsorption theory analysis of experimental water adsorption on illite and montmorillonite clays based on a constrained FHH fit as described above and θ calculated as V∕V_m, where V_m was directly measured from the experimental water adsorption data using BET analysis. The closed circles represent the data fit to the FHH equation (Eq. 8). Resulting A_FHH and B_FHH values are reported in Table 1. For comparison, FHH parameters previously reported in the literature that were determined using other methods are also reported. FHH parameters from analysis of previously reported water adsorption data (Hatch et al., 2014) assuming $\mathit{\theta }={\mathit{\theta }}_{\exp }/{\mathit{\theta }}_{\max }$, and water adsorption (montmorillonite only) analyzed based on $\mathit{\theta }=V/V_m$ are reported. Table 1 also shows the constrained FHH parameters using a surface area and porosity measurement system (Hung et al., 2015) as well as experimental CCN activation measurements of wet- and dry-generated clay minerals (Kumar et al., 2011a, b). In general, the FHH parameters from water adsorption measurements using the method reported here agree more closely with CCN activation-derived FHH parameters compared to those reported previously for the same sample (Hatch et al., 2014). Using Eq. (3), illite and montmorillonite water adsorption isotherms (Fig. 2, solid lines) were calculated based on A_FHH and B_FHH values determined here (Table 1, this study). As shown in Fig. 2, the FHH curves based on analysis of experimental water adsorption appear to fit the experimental data very well and the adsorption isotherms show significantly improved agreement with FHH isotherms calculated from CCN activation measurements of the same clays. Although significant advances toward closure between FHH parameters from water adsorption and CCN activation measurements are demonstrated here, differences remain between FHH parameters determined using different methods. Thus, continued efforts to identify improved agreement between FHH parameters from water adsorption and CCN activation measurements are warranted.

Table 1 A_FHH and B_FHH determined from water adsorption and CCN activation measurements of dry- and wet-generated illite and montmorillonite clays.

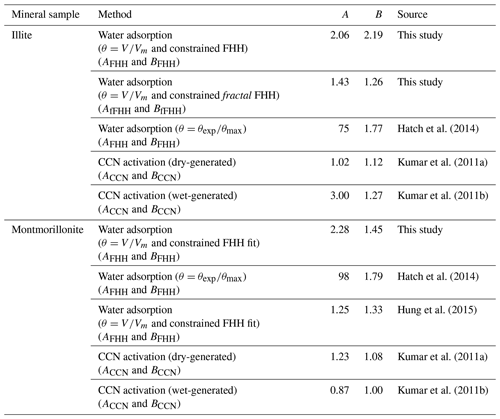
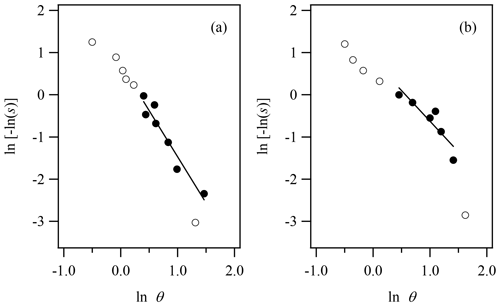
Figure 3 FHH analysis of experimental (a) illite and (b) montmorillonite water adsorption data in which θ was calculated as V∕V_m and V_m was determined from BET analysis. All data (open circles) are shown and the region of the constrained FHH fit (line) is represented by closed circles from 40 % to 90 % RH.

Despite the improved agreement observed upon direct measurement of ML water content and constraining the FHH theory fits to the multilayer adsorption regime, small discrepancies in isotherm structure remain, as shown in Fig. 2. Structural isotherm discrepancies between the two methods are potentially a result of surface heterogeneity and microstructural differences in how space-filling by water adsorption occurs between bulk and aerosol measurements. A recent paper (Laaksonen et al., 2016) suggests that the surface fractal dimension influences water adsorption on insoluble surfaces and thus could help achieve closure between water adsorption and CCN activation measurements. In an effort to account for the observed differences in isotherm structure, the fractal FHH adsorption theory was used to demonstrate the effects of correcting the adsorption isotherm using the surface fractal dimension, D, as discussed in Laaksonen et al. (2016). The fractal FHH adsorption theory is expressed as

$$\begin{array}{}\text{(9)}& \ln S=-A_{\mathrm{fFHH}}{k}^{-B_{\mathrm{fFHH}}}{\left({\displaystyle \frac{V}{V_m}}\right)}^{\frac{-B_{\mathrm{fFHH}}}{\mathrm{3}\text{-D}}},\end{array}$$

according to Laaksonen et al. (2016), where k is a proportionality constant that is equal to unity in the case of a smooth surface and A_fFHH and B_fFHH are the fractal FHH adsorption parameters. D can vary from a value of 2 to 3, where a fractal dimension of 2 represents a completely smooth surface and a value of three represents a surface that fills its space. Here, fractal FHH analysis is restricted to illite clay adsorption data due to the limited data available for montmorillonite in the higher RH range of the multilayer adsorption regime for swelling clays.

The inset of Fig. 4 shows the fractal FHH adsorption theory fit to the experimental water adsorption results for illite clay, again constrained from 40 % to 90 % RH within the multilayer adsorption regime for illite. The resulting fractal FHH adsorption parameters are reported in Table 1 and the resulting k and D parameters are found to be 0.97 and 2.35, respectively. For comparison, Laaksonen et al. (2016) obtained surface fractal dimensions for illite clay ranging from 2.39 to 2.69. Notably, the surface fractal dimension results reported by Laaksonen et al. (2016) are based on clays obtained from different sources and heat treated prior to measurements and thus cannot be directly compared to results reported here. In fractal FHH theory, A_FHH and B_FHH are represented by $A_{\mathrm{fFHH}}{k}^{-B_{\mathrm{fFHH}}}$ and $\frac{-B_{\mathrm{fFHH}}}{\text{3-D}}$, respectively. Applying the resulting k and D values, fractal FHH adsorption analysis gives A_FHH and B_FHH adsorption parameters of 1.48 and 1.94 for illite clay.

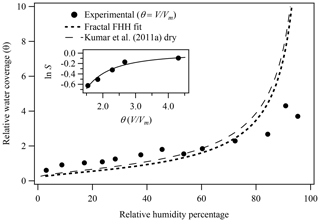
Figure 4 Illite experimental water adsorption isotherm (Hatch et al., 2012) and associated fractal FHH isotherm, where the experimental θ was calculated as V∕V_m and V_m was determined from BET analysis of adsorption isotherm. FHH adsorption isotherms from FHH parameters determined from size-selected CCN measurements of dry-generated illite clay are also shown (Kumar et al., 2011a). The inset shows the constrained fractal FHH isotherm fit to the experimental water adsorption measurements.

Figure 4 also shows the adsorption isotherm generated based on the fractal FHH adsorption parameters obtained compared to the FHH adsorption isotherm from FHH parameters determined from CCN measurements of dry-generated illite clay reported by Kumar et al. (2011a). As shown in Table 1 and Fig. 4, the fractal FHH adsorption analysis results in a modeled isotherm based on experimental water adsorption measurements that exhibit significantly improved agreement with the isotherm obtained from CCN activation measurements of dry-generated illite. This demonstrates that correcting for the surface fractal dimension in experimental water adsorption measurements helps bring closure between aerosol and bulk methods for measuring the uptake of water on insoluble surfaces.

4 Concluding remarks

Experimentally determined FHH water adsorption parameters remain the largest source of uncertainty in assessing the role of insoluble aerosol on liquid cloud formation and the indirect climate effect (Karydis et al., 2012). Thus, accurate measurements of FHH adsorption parameters are necessary to reduce this uncertainty. However, Hatch et al. (2014) have shown that FHH parameters derived from water adsorption measurements (Eq. 1) can differ significantly from values based on FHH-AT analysis of experimental CCN activation measurements (Eq. 2) of the same mineral components (Kumar et al., 2011a, b). The work reported here shows that (1) improved fitting procedures, (2) direct measurement of ML water content, and (3) applying the fractal FHH adsorption model to the experimental water adsorption measurements account for surface microstructure effects and are necessary to obtain closure between experimental water adsorption and CCN-derived FHH parameters.

To assess the improved agreement between FHH adsorption parameters (Table 1) from water adsorption measurements and FHH-AT analysis of dry-generated mineral aerosol CCN activation measurements, a percent difference can be calculated. Results for illite clay indicate that the improved FHH analysis methods described here, including application of the fractal FHH adsorption isotherm, reduce the percentage difference in A_FHH from the value determined based on an FHH-AT assessment of dry-generated aerosol CCN activation from 195 % to ∼33 % difference (Hatch et al., 2014; Kumar et al., 2011a). Thus, as the A_FHH value governs the overall extent of water coverage, the significant reduction in experimental θ based on direct measurements of ML water content from BET analysis of water adsorption is driving improved accuracy of A_FHH values. Results also demonstrate that the agreement between B_FHH values from water adsorption and CCN activation measurements of illite clay also improved (from 45 % to 12 % difference from dry-generated aerosol CCN measurements), particularly upon application of the fractal FHH adsorption model, thereby accounting for space-filling effects of the insoluble surface. Thus, improved agreement between bulk water adsorption and aerosol CCN activation, along with a refined focus on the multilayer adsorption regime and accounting for surface microstructure through direct measurement of the ML water content and application of the fractal FHH adsorption isotherm, demonstrates that closure can be achieved.